Bzoj4823 [Cqoi2017]老C的方块

Posted 2020-09-10 SilverNebula

图论 网络流 最小割 脑洞题

没有题面，懒得手打

 

网络流 最小割

码农题(误)

 

一开始是冲着n<=5000的部分分写了网络流，结果神奇地发现似乎就是正解。

说好的dinic时间复杂度上界$O(V^2 E)$呢……网络流不愧是玄学算法。

 

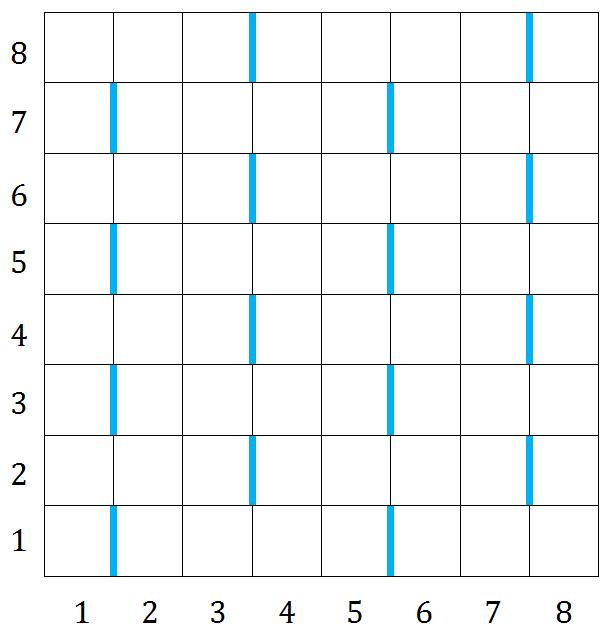
放一张题目里的图

四种图案：

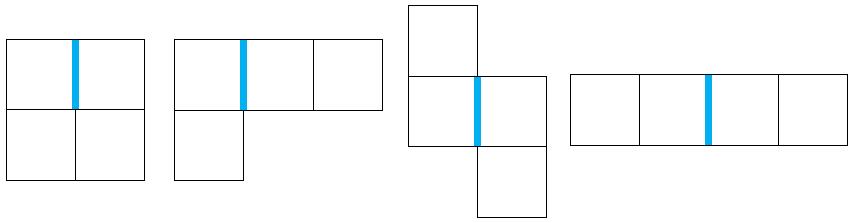
观察这四种图案和它们旋转/翻转以后的样子，可以发现一个共同点：每种图案都是由“中心一条蓝色边和它相邻的两个方块”，以及另外两个邻接的方块组成的

范围画出来就是这个样子：

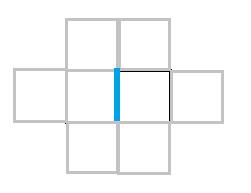
可以发现“另外两个邻接的方块”肯定一个在蓝线左边一个在蓝线右边。

 

先说一种错误的想法：

将每个方块看做一个结点；

左边三个格子如果有方块，从源点向它们连INF边，从它们向中心偏左方块连INF边；

右边三个格子如果有方块，从它们向汇点连INF边，从中心偏右的方块向它们连INF边；

中心偏左的方块向中心偏右的方块连INF边；

按照以上思路，每个方块拆点，入点出点之间连容量为方块权值的边，做最小点割。

然后看一个显然的矛盾：

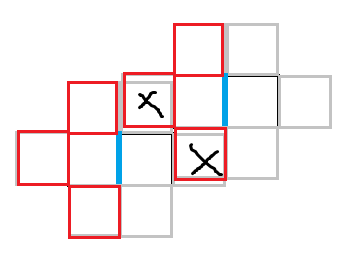
当重合部分有方块的时候，它们就会同时连通源汇点，使得该方块必须被割掉，显然错误。

很可惜样例没有这种情况，博主又傻傻没发现，于是交上去以后愉快地爆零啦

 

正确的做法：

上述问题的解决方法是：重新分类

　　

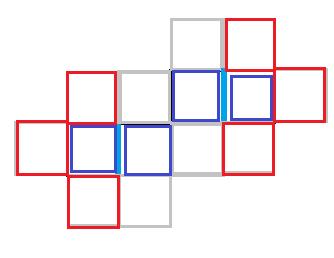
像这样把坐标分成四类，红色的只能入，蓝色的中转，灰色的只能出。

套用到原图上发现没有矛盾。

懒得再画图了，放一张做题时候的草稿。有些乱qwq

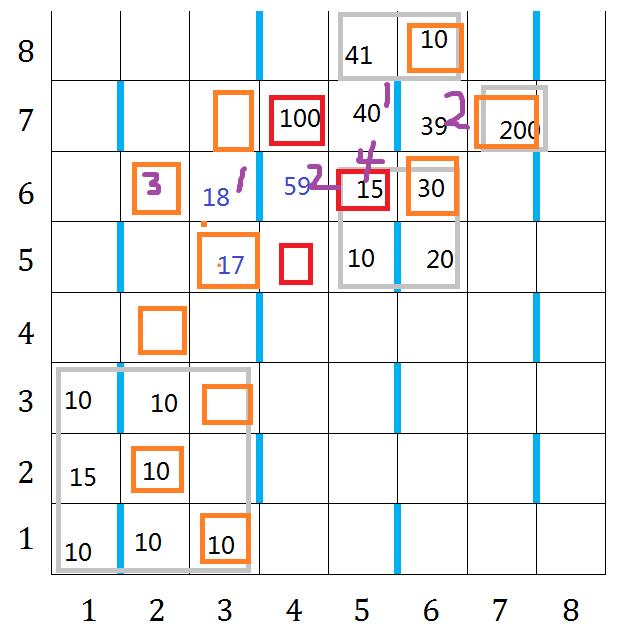
其中灰色方框没有意义，橙色连源点，红色连汇点。

这样就把方格分为四类。每添加一个方块时，查看它四周都有没有方块，如果有，按方格类型讨论连边即可。

——————

给定一个坐标，如何知道它对应哪种格子？按行的奇偶性和列%4的值分类讨论即可

——————

这时候的连边方式有些细节要注意，比如说“中间格”对应的结点不能拆，否则会出现奇怪的方向问题；为了代替拆点限权，两中间格之间的连边应是权值等于min(w[a],w[b])的双向边（同样是为了规避不同流向的权值差异）。

↑画画图就一目了然了。

 

建图建了近百行……过程还有很大优化空间，但是既然过了就不管了（逃）

  1 #include<algorithm>
  2 #include<iostream>
  3 #include<cstring>
  4 #include<cstdio>
  5 #include<cmath>
  6 #include<vector>
  7 #include<queue>
  8 #include<map>
  9 #define LL long long
 10 using namespace std;
 11 const int mx[5]={0,-1,0,1,0};
 12 const int my[5]={0,0,-1,0,1};
 13 const int INF=0x3f3f3f3f;
 14 const int mxn=300010;
 15 int read(){
 16     int x=0,f=1;char ch=getchar();
 17     while(ch<\'0\' || ch>\'9\'){if(ch==\'-\')f=-1;ch=getchar();}
 18     while(ch>=\'0\' && ch<=\'9\'){x=x*10+ch-\'0\';ch=getchar();}
 19     return x*f;
 20 }
 21 struct edge{
 22     int v,nxt,f;
 23 }e[mxn<<2];
 24 int hd[mxn],mct=1;
 25 void add_edge(int u,int v,int w){
 26     e[++mct].v=v;e[mct].nxt=hd[u];e[mct].f=w;hd[u]=mct;return;
 27 }
 28 int S,T;
 29 void insert(int u,int v,int w){
 30 //    printf("u:%d v:%d w:%d\\n",u,v,w);
 31     add_edge(u,v,w);
 32     add_edge(v,u,0);
 33 }
 34 int d[mxn];
 35 bool BFS(){
 36     queue<int>q;
 37     memset(d,0,sizeof d);
 38     q.push(S);
 39     d[S]=1;
 40     while(!q.empty()){
 41         int u=q.front();q.pop();
 42         for(int i=hd[u];i;i=e[i].nxt){
 43             int v=e[i].v;
 44             if(!d[v] && e[i].f){
 45                 d[v]=d[u]+1;
 46                 q.push(v);
 47             }
 48         }
 49     }
 50     return d[T];
 51 }
 52 int DFS(int u,int lim){
 53     if(u==T)return lim;
 54     int f=0,tmp;
 55     for(int i=hd[u];i;i=e[i].nxt){
 56         int v=e[i].v;
 57         if(d[v]==d[u]+1 && e[i].f && (tmp=DFS(v,min(lim,e[i].f)))){
 58             f+=tmp;lim-=tmp;
 59             e[i].f-=tmp;
 60             e[i^1].f+=tmp;
 61             if(!lim)return f;
 62         }
 63     }
 64     d[u]=0;
 65     return f;
 66 }
 67 LL Dinic(){
 68     LL res=0;
 69     while(BFS())res+=DFS(S,INF);
 70     return res;
 71 }
 72 //
 73 int PD(int x,int y){//判断是否在关键边旁边 
 74     if(y%4==0){
 75         if((x&1)==0)return 2;//right
 76         else return 4;//outpos
 77     }
 78     if(y%4==1){
 79         if(x&1)return 1;//left
 80         else return 4;//outpos
 81     }
 82     if(y%4==2){
 83         if(x&1)return 2;//right
 84         else return 3;//inpos
 85     }
 86     if(y%4==3){
 87          if((x&1)==0)return 1;//left
 88          else return 3;//inpos
 89     }
 90     return 0;
 91 }
 92 map<pair<int,int>,int>mp;
 93 struct block{
 94     int x,y;
 95     int w;
 96 }b[mxn];
 97 int C,R,n;
 98 int Tct[mxn];
 99 void Build(int id){
100 //    printf("insert:#%d\\n",id);
101     int s=PD(b[id].x,b[id].y);
102     for(int k=1;k<=4;k++){
103         int nx=b[id].x+mx[k];
104         int ny=b[id].y+my[k];
105         if(nx>0 && nx<=R && ny>0 && ny<=C){
106             int v=mp[make_pair(nx,ny)];
107             if(!v)continue;
108             int t=PD(nx,ny);
109 /*            printf("u:%d v:%d s:%d t:%d\\n",id,v,s,t);
110             printf("x1:%d y1:%d x2:%d y2:%d\\n",
111                 b[id].x,b[id].y,nx,ny);
112             printf("s:%d t:%d\\n\\n",s,t);*/
113             if(s==1 && t==2){
114                 add_edge(id,v,min(b[id].w,b[v].w));
115                 add_edge(v,id,min(b[id].w,b[v].w));
116             }
117             if(s==2 && t==1){
118                 add_edge(id,v,min(b[id].w,b[v].w));
119                 add_edge(v,id,min(b[id].w,b[v].w));
120             }
121             if(s==1 && t==3){
122                 insert(S,v,INF);
123                 insert(v+n,id,INF);
124             }
125             if(s==1 && t==4){
126                 insert(id,v,INF);
127                 insert(v+n,T,INF);
128             }
129             if(s==2 && t==3){
130                 insert(S,v,INF);
131                 insert(v+n,id,INF);
132             }
133             if(s==2 && t==4){
134                 insert(id,v,INF);
135                 insert(v+n,T,INF);
136             }
137             if(s==3 && t==1){
138                 insert(S,id,INF);
139                 insert(id+n,v,INF);
140             }            
141             if(s==3 && t==2){
142                 insert(S,id,INF);
143                 insert(id+n,v,INF);
144             }
145             if(s==4 && t==1){
146                 insert(id+n,T,INF);
147                 insert(v,id,INF);
148             }
149             if(s==4 && t==2){
150                 insert(id+n,T,INF);
151                 insert(v,id,INF);
152             }
153         }
154     }
155     mp[make_pair(b[id].x,b[id].y)]=id;
156 //    printf("\\n");
157     return;
158 }
159 void solve(){
160     for(int i=1;i<=n;i++){
161         int t=PD(b[i].x,b[i].y);
162         if(t==1 || t==2)continue;
163         add_edge(i,i+n,b[i].w);
164         add_edge(i+n,i,0);
165     }
166     LL res=Dinic();
167     printf("%lld\\n",res);
168     return;
169 }
170 int main(){
171 //    freopen("block.in","r",stdin);
172 //    freopen("block.out","w",stdout);
173     int i,j;
174     C=read();R=read();n=read();
175     for(i=1;i<=n;i++){
176         b[i].y=read();b[i].x=read();//行列顺序相反 
177         b[i].w=read();
178     }
179     S=0;T=n*2+1;
180     for(i=1;i<=n;i++)Build(i);
181     solve();
182     return 0;
183 }