3论二进制减法

Posted 2020-09-09 愚智

根据上面的加法，我们觉得的确门逻辑能解决这种加法的进位问题。可是减法呢？

减法涉及到借位，并且还要判断位数能不能借，不能借得向更高的位去借，这种逻辑貌似门实现起来复杂度相当之高？其实不然

如何避免这种复杂的借位，最好的办法，向最高位的再高一位借一位，那么就涉及不到那么多位的借位了。也就是说8位，我们借第九位的一位。所以得到

253-176=77的情况下，我们可以借个1000，因为减1000只涉及到最高位的门逻辑，然后用999减去176，因为999和176都是三位，用相同数量的门电路可以实现了，结果再加1.而176我们就叫做999的补数。

现在结果编程计算253+999-176+1-1000的情况。

 

但是如果是176-253呢？你可能会想到跟前面一样，176+999-253+1-1000，但是923-1000导致了借位，这样我们只操作最高位高一位的门逻辑是无法实现的。我们不如直接176+999-253-999，让它们都用相同数据量级的门逻辑计算，不过922-999这一步我们把它变成999-922，然后再加个负符号。

 

现在我们演化成二进制来看看。

253-176 变成二进制位

 1 1 1 1 1 1 0 1

-1 0 1 1 0 0 0 0

—————————

  ? ? ? ? ? ? ? ?

第一步、我们使用11111111（255）减去减数：

 1 1 1 1 1 1 1 1

-1 0 1 1 0 0 0 0

--------------------

 0 1 0 0 1 1 1 1

这种计算对于门电路来说很简单，只需要对减数求反，将0变成1，1变成0.

第二步、把被减数和刚才我们求得的对1的补数相加：

  1 1 1 1 1 1 0 1

+0 1 0 0 1 1 1 1

-------------------

1 0 1 0 0 1 1 0 0

第三步、对上面结果+1

  1 0 1 0 0 1 1 0 0

+　　　　　　　　1

-----------------------

  1 0 1 0 0 1 1 0 1

第四步，减去100000000（256）

  1 0 1 0 0 1 1 0 1

- 1 0 0 0 0 0 0 0 0

-----------------------

        1 0 0 1 1 0 1

即等于77.

 

 

现在我们来算下176-253

二进制表示为

  1 0 1 1 0 0 0 0

- 1 1 1 1 1 1 0 1

--------------------

  ? ? ? ? ? ? ? ?

第一步，用11111111减去减数，得到对1的补数

  1 1 1 1 1 1 1 1

- 1 1 1 1 1 1 0 1

-------------------

  0 0 0 0 0 0 1 0

第二步，将减数对1的补数与被减数相加：

  1 0 1 1 0 0 0 0

+0 0 0 0 0 0 1 0

---------------------

  1 0 1 1 0 0 1 0

第三步、用11111111减去结果

  1 1 1 1 1 1 1 1

- 1 0 1 1 0 0 1 0

--------------------

  0 1 0 0 1 1 0 1

结果是77，但是答案应该是-77

 

 

现在我们可以来改造上面一章的加法器了，为了不过于复杂，我们先涉及减数小于被减数的操作。

上一章我们的加法器是这样的：

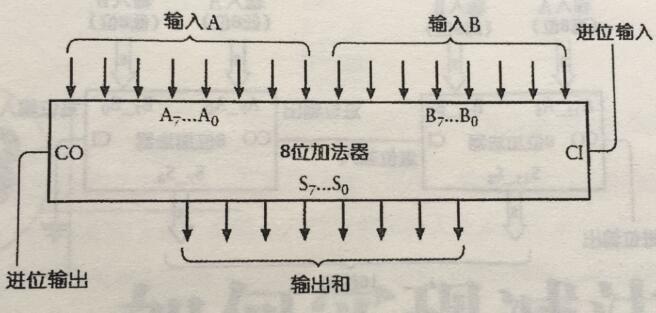
我们得增设一个标识，来表明它是一个加法还是减法。我们的目的是做一个既能做加法，也能做减法的逻辑器。

首先我们得对B进行取反，且仅当减法的时候进行取反，这样就不会影响到加法，

我们首先想下异或门的工作方式：

XOR	0	1
0	0	1
1	1	0

 

 

改造图如下：

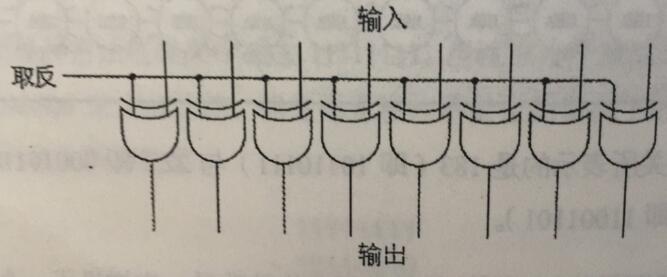
取反就是我们的加法减法标识，我们定义标识为0时是加法，1是减法。当0加法的时候，输入和输出是不变的，如果是1减法的时候，那么正好是一个取反的状态。

我们将8个异或门组成的器件，称为求补器：

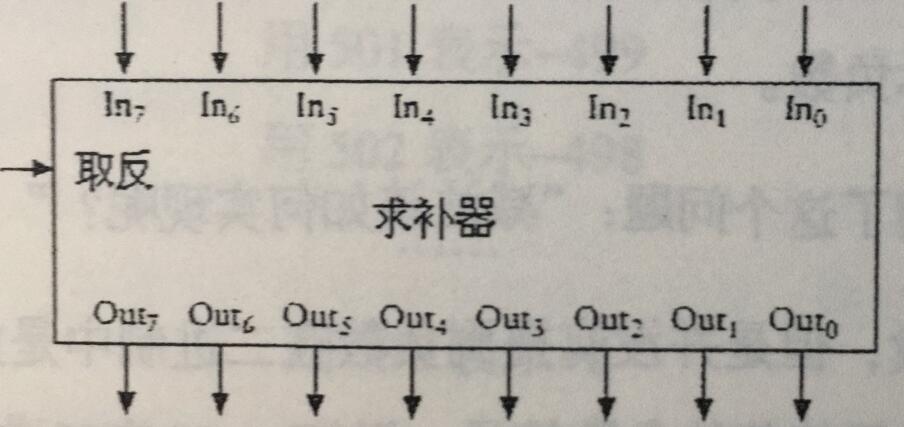
现在我们组合的连接如下：

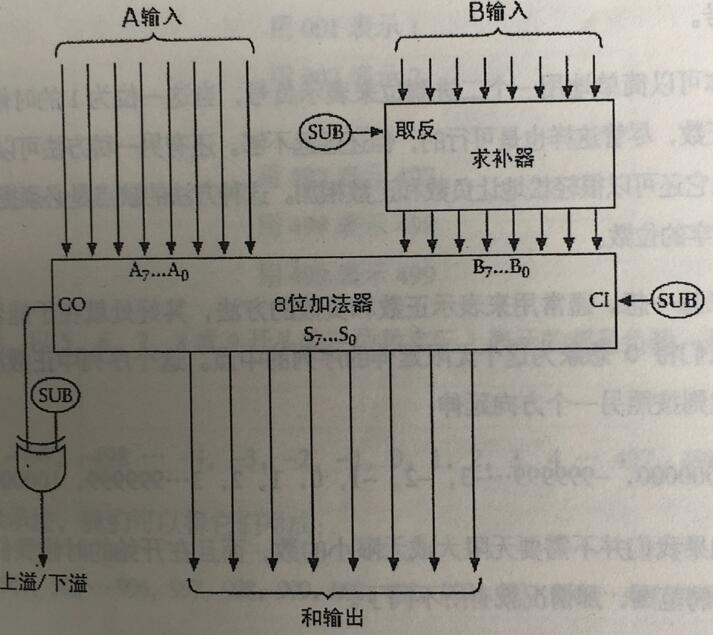
SUB就是我们的加法减法的标识位，0加法，1减法。在B输入的时候，我们进行减法求反，达到被11111111减去的效果，通过最右边的SUB来达到对减法结果加1的效果，对加法没影响。通过最左边的异或门和sub来达到上溢（大于255）/下溢（负数）的结果，SUB为0加法的时候，对输出没影响，CO为1代表大于255。当减法的时候，SBU为1，CO输出1，这个门逻辑组合就会得到0，达到减去100000000的效果，如果CO输出0，代表了负数（如5-8=9+1-10+5-8=9-8+5+1-10=6-10,被减数只要小于减数，最后推算的这个被减数6是无论如何十位是不可能得到1的）经过这个门逻辑组合就会得到1，所以这个1就是下溢（负号）的标识。

 

 

现在我们的减法器是做好了，那么接下来我们讨论下这个负数如何在我们的二进制里面表示呢？

我们平常使用的系统都是在一定范围内的数字，所以我们不用求无限大的数值表示。

比如我们现在需要表示-500到499之间的数。我们都要用正数表示，因为我们二进制系统不支持-这个符号。我们就用三位数来表示这些数字。

500表示-500，501表示-499......999表示-1，000表示0，001表示1......499表示499

这样我们就形成了一个循环，好处是我们-1+1=0的情况用正数来表示999+1=1000，1由于是第四位，会被舍弃，就会得到结果0，

 这种标记的方法称为10的补数。

如果你有一个余额为143块的账户，你用了78元。-78对10的补数是999-078+1=65（忽略溢出）。如果我们用超额的用了150块，-150对10的补数是850，就等于915，就是新账户的余额，在我们的表示中就是-85块。