Codeforces 622F 「数学数论」「数学规律」

Posted 2020-06-18 徐暾

题意：

给定n和k，求

1 ≤ n ≤ 10⁹, 0 ≤ k ≤ 10⁶

思路：

题目中给的提示是对于给定的k我们可以求出一个最高次为k+1的关于n的通项公式。

根据拉格郎日插值法，我们可以通过k+2个离散的点来确定这个通项。所以求出前k+2项，然后就可以确定公式。

拉格郎日差值法传送门：http://www.guokr.com/post/456777/

最后得出的公式是酱紫的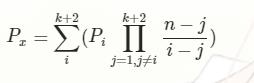：（公式来自卿学姐博客）

然后问题来了，有除法如何搞定模运算...这个就用到逆元的运算了，逆元的定义就是大家都学过的离散数学里边的那个定义，求解方法有两种，一种是根据扩展欧几里得，构造ax+by=1（mod某数），如果取模的某数是一个素数的话可以根据费马小定理a^(p-1)=1(mod某数)，结合快速幂求解。

注意有j！=i的条件...所以要求的逆元数是两个，好好理解下这个式子可以用阶乘优化复杂度。

传送门：http://www.cnblogs.com/james47/p/3871782.html

坑点：

注意逆元的运算应该放到等式的前边。然后注意阶乘的正负。

代码：（基本是跟卿学姐一个模子刻出来的==

#include<bits/stdc++.h>
using namespace std;
long long mod=(1e9)+7;
long long p[1000050];
long long fac[1000050];
long long quick_pow(long long a,long long b,long long m){
    long long tmp=1;
    while(b){
        if(b&1){
            tmp*=a;
            tmp%=m;
        }
        a*=a;
        a%=m;
        b>>=1;
    }
    return tmp;
}
int main()
{
    long long n,k;
    cin>>n>>k;
    for(int i=1;i<=k+2;i++){
        p[i]=(p[i-1]+quick_pow(i,k,mod))%mod;
    }
    fac[0]=1;
    for(int i=1;i<=1000010;i++){
        fac[i]=fac[i-1]*i;
        fac[i]%=mod;
    }
    if(n<=k+2){
        cout << p[n] << endl;
        return 0;
    }
    long long chang=1;
    for(int i=1;i<=k+2;i++){
        chang*=n-i;
        chang%=mod;
    }
    long long ans=0;
    for(int i=1;i<=k+2;i++){
        long long a=quick_pow(n-i,mod-2,mod);
        long long b=quick_pow((fac[i-1]*fac[k+2-i])%mod,mod-2,mod);
        if((k+2-i)%2)b=-b;
        ans =(ans + p[i]*chang%mod*b%mod*a)%mod;//这句一定要注意逆元运算先
    }
    cout << ans << endl;
}