Codeforces 451 E. Devu and Flowers（组合数学，数论，容斥原理）

Posted 2021-01-16 blog-dr-j

传送门

解题思路：

假如只有 s 束花束并且不考虑 f ，那么根据隔板法的可重复的情况时，这里的答案就是

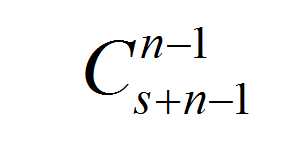
假如说只有一个 f 受到限制，其不合法时一定是取了超过 f 的花束

那么根据组合数，我们仍然可以算出其不合法的解共有：

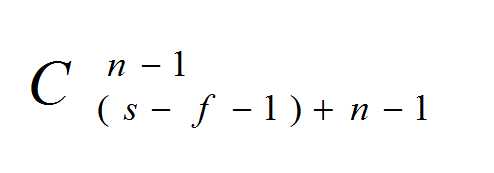
最后，由于根据容斥，减两遍的东西要加回来，那么含有偶数个 f 的项为正，奇数个时为负。

答案就是：

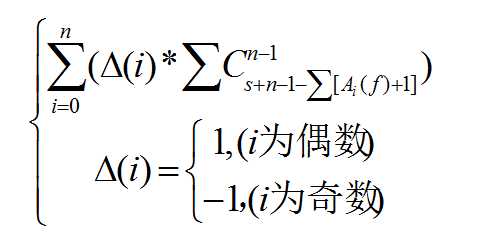
搜索答案，使用Lucas定理，计算组合数上下约去。

代码：

 1 #include<cstdio>
 2 #include<cstring>
 3 #include<algorithm>
 4 typedef long long lnt;
 5 const lnt mod=(lnt)(1e9+7);
 6 int n;
 7 lnt s,ans;
 8 lnt f[1000];
 9 lnt ksm(lnt x,lnt y)
10 {
11     lnt ans=1;
12     while(y)
13     {
14         if(y&1)
15             ans=ans*x%mod;
16         x=x*x%mod;
17         y=y/2;
18     }
19     return ans;
20 }
21 lnt Lucas(lnt n,lnt m)
22 {
23     if(n<mod&&m<mod)
24     {
25         if(n<m)    return 0;
26         if(n==m)return 1;
27         if(m==0)return 1;
28         lnt nj=1,mj=1;
29         lnt a=n-m,b=m;
30         if(a>b)
31             std::swap(a,b);
32         lnt i=b+1;
33         while(i<=n)
34         {
35             nj=(nj*i)%mod;
36             i++;
37         }
38         i=2;
39         while(i<=a)
40         {
41             mj=(mj*i)%mod;
42             i++;
43         }
44         return ksm(mj,mod-2)*nj%mod;
45     }
46     return Lucas(n%mod,m%mod)*Lucas(n/mod,m/mod)%mod;
47 }
48 lnt dle(lnt x)
49 {
50     return (((1&x)^1)<<1)-1;
51 }
52 void dfs(int p,int l,lnt sum)
53 {
54     if(p==n+1)
55     {
56         ans=(ans+dle(l)*Lucas(s-sum+n-1,n-1))%mod;
57         return ;
58     }
59     dfs(p+1,l,sum);
60     dfs(p+1,l+1,sum+f[p]+1);
61     return ;
62 }
63 int main()
64 {
65     scanf("%d%I64d",&n,&s);
66     for(int i=1;i<=n;i++)
67         scanf("%I64d",&f[i]);
68     ans=0;
69     dfs(1,0,0);
70     printf("%I64d
",(ans%mod+mod)%mod);
71     return 0;
72 }