用数学语言说一下动态规划求数列最长递增子序列的解

Posted 2023-04-18

用数学语言说一下动态规划求数列最长递增子序列的解以及为什么是n㏒n时间级别，还有该方法的可行性，不要代码，本身还没有学编程，是数学中一道题，我想知道他的思想，代码都是次要的，网上查的都是一串串代码，求好心人讲一下

对于序列 L=a1,a2,a3,a4,…,an,我们总能够找到它的最长的一组或几组递增子序列 LIS=ak1,ak2,ak3,ak4,…,akm；
要知道a1---an的最长的递增子序列，我们只需要知道a1---an-1的最长的递增子序列就行了，于是就得到了求最长递增子序列的公式：
b[k]=max(max(b[j]|a[j]<a[k],j<k)+1,1)
这里的b[k]指的是，下标为k的元素之前包括ak的最长递增子序列。
首先，我们看一下公式中的这个部分： max(b[j]|a[j]<a[k],j<k)+1
“+1”不难理解就是加上当前的这个元素，因为当前的这个元素也是当前求得的最长递增子序列的一部分，而且是最后一个元素。
max(b[j]|a[j]<a[k],j<k)指的是a[k]之前的元素构成的最长递增子序列，而它的值就是b[j]。
然后公式的最后有一个1，这个1指的是，如果a[k]之前的最长递增子序列的长度为0，那么b[k]就是其自身，也就是说b[k]==1。 参考技术A 对于序列 L=a1,a2,a3,a4,…,an,我们总能够找到它的最长的一组或几组递增子序列 LIS=ak1,ak2,ak3,ak4,…,akm；
要知道a1---an的最长的递增子序列，我们只需要知道a1---an-1的最长的递增子序列就行了，于是就得到了求最长递增子序列的公式：
b[k]=max(max(b[j]|a[j]<a[k],j<k)+1,1)
这里的b[k]指的是，下标为k的元素之前包括ak的最长递增子序列。
首先，我们看一下公式中的这个部分： max(b[j]|a[j]<a[k],j<k)+1
“+1”不难理解就是加上当前的这个元素，因为当前的这个元素也是当前求得的最长递增子序列的一部分，而且是最后一个元素。
max(b[j]|a[j]<a[k],j<k)指的是a[k]之前的元素构成的最长递增子序列，而它的值就是b[j]。
然后公式的最后有一个1，这个1指的是，如果a[k]之前的最长递增子序列的长度为0，那么b[k]就是其自身，也就是说b[k]==1。

求单调递增最长子序列长度

设计O(n*n)时间的算法，求n个数组成的序列的单调递增最长子序列长度

这道题在算法分析课本中属于课后习题，许多人做过，这道题是我真正体会到动态规划的思想的一道题，下面给出一个简单的思路!

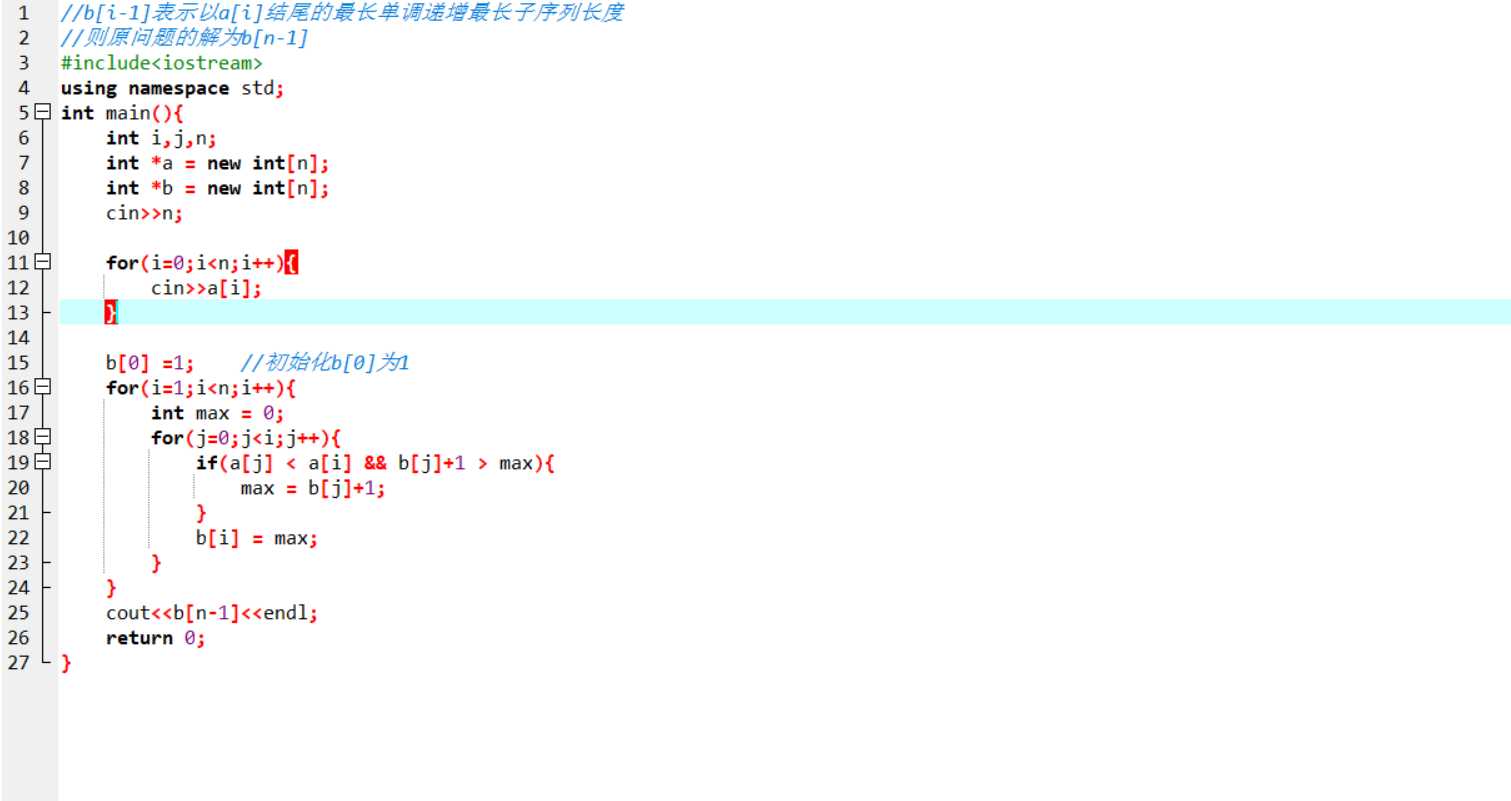
记a[i]表示输入的序列，b[i-1]表示以a[i]结尾的序列的单调递增最长子序列,则原问题的解为b[n-1]；