线性规划与网络流24题●09方格取数问题&13星际转移问题

Posted 2020-09-07 *ZJ

●（做codevs1908时，发现测试数据也涵盖了1907，想要一并做了，但因为“技术”不佳，搞了一上午）

●09方格取数问题（codevs1907  方格取数3）

• 
• 想了半天，也没成功建好图；
• 无奈下参考题解，说是本题要求二分图点权最大独立集，然后可以由结论：“最大点权独立集 = 所有点权 - 最小点权覆盖集 = 所有点权 - 最小割集 = 所有点权 - 网络最大流”转化到求最大流（我真的很懵逼，但又感觉很有道理）；
• 下面附上solution：（自己领悟吧）
• 
• （不懂那个鬼结论的我就用那个结论建了个图，跑了个Dinic。）

●13星际转移问题（codevs 1908）

• （这个题的要比上一个好想一些。（因为上一题的鬼结论我真不知道））
• 
• 思路：
• 本题的建图比较有趣，要把每个空间站按天数进行建点和连边；
• 建图:
• 1.原点（s）到地球（ear）有一条容量为k的边；（表示要送出k个人民）
• 2.月球（yue）到汇点（t）有一条容量为INF的边；
• 3.每个空间站的前一天的点到该空间站的后一天有一条容量为INF的边；（表示人民可以待在空间站里度过一天又一天）
• 4.若一个飞船在前一天在某一空间站（或地球），后一天在另一个空间站（或月球），则在对应的两个点间连一条有向边，容量为飞船的载重；（表示前一天某一空间站（或地球）的几个人民可以通过一个飞船坐到后一天的另一个空间站（或月球）；
• 以题目的样例为例，上一张图帮助理解；
• 
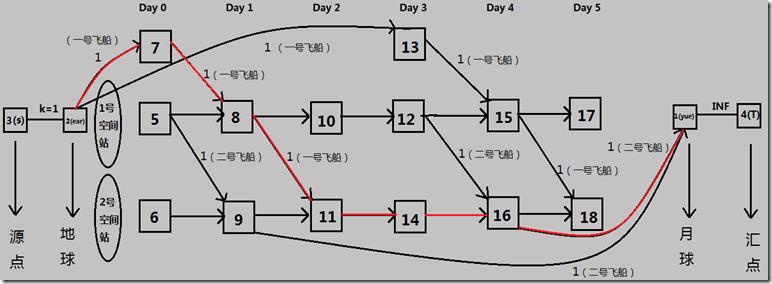
• 上图中：
• 方框为点，里面的数字为编号；
• 黑色箭头为边，上的数字为容量，（未标的均为INF）；
• 红色路径为最大的可行流。
• （建图方法解决后，但还有一个问题，Day是未知的，该怎么确定点有多少呢？）
• 方法：枚举天数或二分天数，然后跑个最大流判断是否能将人民送完（即汇点的流入量是否等于k）；
• 选择：枚举天数：
• 原因：改图比较特殊，若用枚举天数的方法，只需每次在前一次的图上加新点，连新边即可，一直到找到答案。若用二分的话，则需要每次重新建图。
• （当然，在开始枚举天数之前，先用并查集检查一下人民能否从地球到月球。）
• 总：枚举+Dinic（找最大流）+并查集（e，只是用来检查的）

●代码(为了AC掉codevs1908，把两份代码怼到一起了)：

#include<iostream>
#include<cstdio>
#include<cstring>
#define INF 0x3f3f3f3f
using namespace std;
int n,m,k,yue=1,ear=2,sz=4,ent=2,aim,tot,s,t;
int sps[30][30],cw[30][2],ld[30],ls[30],head[30000],h[30000],q[30000];
int fa[30];
struct edge{
	int to,cap,next;
}e[300000];
bool special_read()
{
	char s[100];
	gets(s);
	int a[4]={0},o=1;
	int len=strlen(s);
	for(int i=0;i<len;i++)
	{
		if(\'0\'<=s[i]&&s[i]<=\'9\') a[o]=a[o]*10+s[i]-\'0\';
		else if(a[o]) o++; 
	}
	n=a[1];m=a[2];
	return k=a[3];
}
int read(int &o)
{
	int x=0,f=1; char ch=getchar();
	while(ch<\'0\'||ch>\'9\'){if(ch==\'-\') f=-1;ch=getchar();}
	while(\'0\'<=ch&&ch<=\'9\') {x=x*10+ch-\'0\';ch=getchar();}
	o=x*f;
}
void add_edge(int u,int v,int cap)
{
	e[ent]=(edge){v,cap,head[u]};head[u]=ent++;
	e[ent]=(edge){u,0,head[v]};head[v]=ent++;
}
void make_new_edge(int day)
{
	for(int i=3;i<=n+3-1;i++) add_edge(ld[i],++sz,INF),ld[i]=sz;
	for(int i=1;i<=m;i++)
	{
		int t=day%cw[i][1],o=sps[i][t];
		if(o==ear) add_edge(ear,++sz,cw[i][0]),ls[i]=sz;
		else if(o==yue) add_edge(ls[i],yue,cw[i][0]),ls[i]=0;
		else 
		{
			if(ls[i])add_edge(ls[i],ld[o],cw[i][0]);
			ls[i]=ld[o];
		}
	}
}
bool bfs(int s,int t)
{
	memset(h,0,sizeof(h));
	int l=0,r=1;q[1]=s;h[s]=1;
	while(l<r)
	{
		int u=q[++l];
		for(int i=head[u];i;i=e[i].next)
		{
			int v=e[i].to;
			if(h[v]||!e[i].cap) continue;
			h[v]=h[u]+1; q[++r]=v;
		}
	}
	return h[t];
}
int dfs(int u,int res,int t)
{
	if(u==t) return res;
	int flowout=0,f;
	for(int i=head[u];i;i=e[i].next)
	{
		int v=e[i].to;
		if(!e[i].cap||h[v]!=h[u]+1) continue;
		f=dfs(v,min(res,e[i].cap),t);
		e[i].cap-=f; e[i^1].cap+=f;
		flowout+=f; res-=f;
		if(!res) break;
	}
	if(!flowout) h[u]=-1;
	return flowout;
}
int Dinic(int s,int t)
{
	while(bfs(s,t))
	{
		aim+=dfs(s,INF,t);
	}
	return aim;
}
void check_and_add(int a,int b,int c,int d)
{
	c+=a; d+=b;
	if(c==0||c==n+1||d==0||d==m+1) return;
	int u=(a-1)*m+b,v=(c-1)*m+d;
	add_edge(u,v,INF);
}
int find(int x)
{
	if(fa[x]!=x) return fa[x]=find(fa[x]);
	return x;
}
void unio(int x,int y)
{
	int fx=find(x),fy=find(y);
	if(fx!=fy) fa[fy]=fx;
}
void _1908()
{
	for(int i=1;i<=25;i++) fa[i]=i;
	for(int i=1;i<=m;i++)
	{
		read(cw[i][0]);read(cw[i][1]);
		for(int j=0;j<cw[i][1];j++) 
		{
			read(sps[i][j]);
			sps[i][j]+=2;
			if(j) 
			for(int jj=0;jj<j;jj++)
			 unio(sps[i][jj],sps[i][j]);
		}
	}
	if(find(yue)!=find(ear)) printf("0");
	else
	{
		int day=0;
		add_edge(3,ear,k); add_edge(yue,4,INF);
		for(int i=3;i<=n+3-1;i++) ld[i]=++sz;
		for(int i=1;i<=m;i++)
		{
			int o=sps[i][0];
			if(o==ear) add_edge(ear,++sz,cw[i][0]),ls[i]=sz;
			else if(o!=yue) ls[i]=ld[o];
		}
		while(1)
		{
			++day;
			make_new_edge(day);
			if(Dinic(3,4)==k) { printf("%d",day); break;}
		}
			
	}
}
void _1907()
{
	int x,co=0;
	s=n*m+1;t=n*m+2;
	for(int i=1;i<=n;i++)
	for(int j=1;j<=m;j++)
	{
		co=(i+j)%2;
		int u=(i-1)*m+j;scanf("%d",&x); tot+=x;
		if(!co)
		{
			add_edge(s,u,x);
			check_and_add(i,j,-1,0);
			check_and_add(i,j,1,0);
			check_and_add(i,j,0,-1);
			check_and_add(i,j,0,1);	
		} 
		else add_edge(u,t,x);
	}
	printf("%d",tot-Dinic(s,t));
}
int main()                                 
{
	if(special_read()) _1908();
	else _1907(); 
	
	return 0;	
}