如何衡量两个“任意数据集”间的相似度？

Posted 2023-04-11

参考技术A 对于两个数据集 和 。若存在矩阵 和 ，使得 ， 可以通过 经过若干次线性变换得到，这表明了 中的信息完全蕴含在 中。此时，相对于 ， 中的信息是冗余的。这种冗余既可以体现在维度上，即 中的样本分布在一个高维空间中的低维流形上，也可以体现在样本上，即 中存在一些非常相似的样本。矩阵 和 分别在样本层面和特征层面使 与 对齐。同样的，若存在矩阵 和 ，使得 ，则表明 中的信息完全蕴含在 中。但是对于一般的两个数据集 和 ，不太可能会出现 中信息完全蕴含于 或 中信息完全蕴含于 的情况。因此可以通过考虑两个数据集在线性变换下的信息损失来度量两个数据集的差异（相似度）。具体的，可以考虑求解以下优化问题： 优化过程也是使两个数据集在样本层面和特征层面对齐的过程，求解优化问题得到的结果可以作为两个数据集的差异度量。若想得到 范围内的相似性度量，对差异度量做以下变换即可。

智能推荐算法基础-余弦相似度计算

余弦相似度用向量空间中两个向量夹角的余弦值作为衡量两个个体间差异的大小。余弦值越接近1，就表明夹角越接近0度，也就是两个向量越相似，这就叫"余弦相似性"。

我们知道，对于两个向量，如果他们之间的夹角越小，那么我们认为这两个向量是越相似的。余弦相似性就是利用了这个理论思想。它通过计算两个向量的夹角的余弦值来衡量向量之间的相似度值。余弦相似性推导公式如下：

 

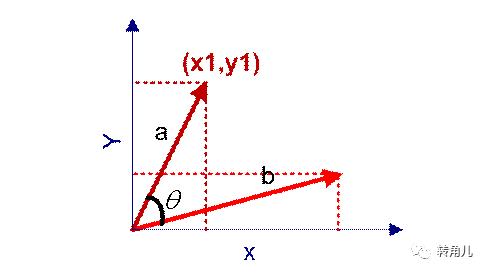
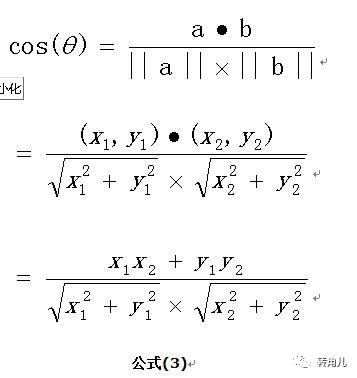
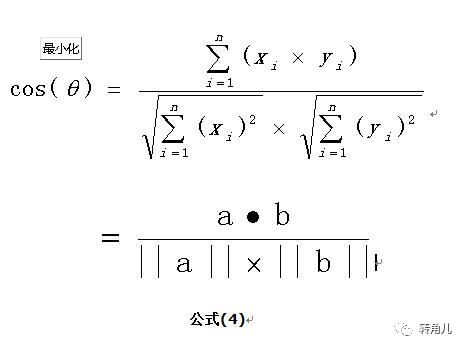
【下面举一个例子，来说明余弦计算文本相似度】

    举一个例子来说明，用上述理论计算文本的相似性。为了简单起见，先从句子着手。

       句子A：这只皮靴号码大了。那只号码合适

句子B：这只皮靴号码不小，那只更合适

怎样计算上面两句话的相似程度？

基本思路是：如果这两句话的用词越相似，它们的内容就应该越相似。因此，可以从词频入手，计算它们的相似程度。

第一步，分词。

句子A：这只/皮靴/号码/大了。那只/号码/合适。

句子B：这只/皮靴/号码/不/小，那只/更/合适。

第二步，列出所有的词。

这只，皮靴，号码，大了。那只，合适，不，小，很

第三步，计算词频。

句子A：这只1，皮靴1，号码2，大了1。那只1，合适1，不0，小0，更0

句子B：这只1，皮靴1，号码1，大了0。那只1，合适1，不1，小1，更1

第四步，写出词频向量。

句子A：(1，1，2，1，1，1，0，0，0)

　　句子B：(1，1，1，0，1，1，1，1，1)

到这里，问题就变成了如何计算这两个向量的相似程度。我们可以把它们想象成空间中的两条线段，都是从原点（[0, 0, ...]）出发，指向不同的方向。两条线段之间形成一个夹角，如果夹角为0度，意味着方向相同、线段重合,这是表示两个向量代表的文本完全相等；如果夹角为90度，意味着形成直角，方向完全不相似；如果夹角为180度，意味着方向正好相反。因此，我们可以通过夹角的大小，来判断向量的相似程度。夹角越小，就代表越相似。

使用上面的公式(4)

 

计算两个句子向量

句子A：(1，1，2，1，1，1，0，0，0)

和句子B：(1，1，1，0，1，1，1，1，1)的向量余弦值来确定两个句子的相似度。

计算过程如下：

 

计算结果中夹角的余弦值为0.81非常接近于1，所以，上面的句子A和句子B是基本相似的