计算两个向量的余弦相似度
Posted AI浩
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了计算两个向量的余弦相似度相关的知识,希望对你有一定的参考价值。
文章目录
摘要
余弦相似度是判断两个向量相似度常用的算法,我在做行人重识别的时候,用到了余弦相似度的算法,记录一下。
基本概念
余弦相似度算法:一个向量空间中两个向量夹角间的余弦值作为衡量两个个体之间差异的大小,余弦值接近1,夹角趋于0,表明两个向量越相似,余弦值接近于0,夹角趋于90度,表明两个向量越不相似。
总之,相似度越小,距离越大。相似度越大,距离越小。
数学原理
所以余弦的计算公式如下:
cos
θ
=
a
2
+
b
2
−
c
2
2
a
b
\\cos \\theta=\\fraca^2+b^2-c^22 a b
cosθ=2aba2+b2−c2
a,b,c 是三个边的长度。
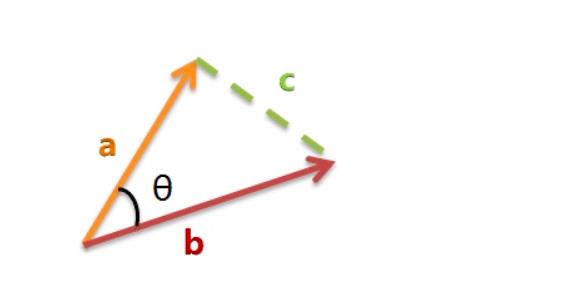
在直角坐标系中,向量表示的三角形的余弦函数是怎么样的呢?下图中向量a用坐标(x1,y1)表示,向量b用坐标(x2,y2)表示。
向量
a
\\mathrma
a 和向量
b
\\mathrmb
b 在直角坐标中的长度为
c
=
x
1
2
+
y
1
2
c=\\sqrtx_1^2+y_1^2
c=x12+y12,
b
=
x
2
2
+
y
2
2
b=\\sqrtx_2^2+y_2^2
b=x22+y22 , 向量
a
\\mathrma
a 和向量
b
\\mathrmb
b 之间的距离我们用向量
c
\\mathrmc
c 表示,就是上图中的黄色直线,那么向 量 c 在直角坐标系中的长度为
c
=
(
x
2
−
x
1
)
2
+
(
y
2
−
y
1
)
2
\\mathrmc=\\sqrt\\left(x_2-x_1\\right)^2+\\left(y_2-y_1\\right)^2
c=(x2−x1)2+(y2−y1)2 , 将 a , b , c 带入三角函数的公式中得到如下的公式:
cos
(
θ
)
=
a
2
+
b
2
−
c
2
2
a
b
=
x
1
2
+
y
1
2
+
x
2
2
+
y
2
2
−
(
x
2
−
x
1
)
2
−
(
y
2
−
y
1
)
2
2
x
1
2
+
y
1
2
∗
x
2
2
+
y
2
2
=
x
1
∗
x
2
+
y
1
∗
y
2
x
1
2
+
y
1
2
∗
x
2
2
+
y
2
2
\\beginarrayl \\cos (\\theta)=\\fraca^2+b^2-c^22 a b=\\fracx_1^2+y_1^2+x_2^2+y_2^2-\\left(x_2-x_1\\right)^2-\\left(y_2-y_1\\right)^22 \\sqrtx_1^2+y_1^2 * \\sqrtx_2^2+y_2^2 \\\\ =\\fracx_1 * x_2+y_1 * y_2\\sqrtx_1^2+y_1^2 * \\sqrtx_2^2+y_2^2 \\endarray
cos(θ)=2aba2+b2−c2=2x12+y12∗x22+y22x12+y12+x22+y22−(x2−x1)2−(y2−y1)2=x12+y12∗x22+y22x1∗x2+y1∗y2

cos θ = ∑ i = 1 n ( A i × B i ) ∑ i = 1 n ( A i ) 2 × ∑ i = 1 n ( B i ) 2 = A ⋅ B ∣ A ∣ × ∣ B ∣ \\beginaligned \\cos \\theta & =\\frac\\sum_i=1^n\\left(A_i \\times B_i\\right)\\sqrt\\sum_i=1^n\\left(A_i\\right)^2 \\times \\sqrt\\sum_i=1^n\\left(B_i\\right)^2 \\\\ & =\\fracA \\cdot B|A| \\times|B| \\endaligned cosθ=∑i=1n(A20-余弦相似度及其R实现