Spark笔记(1) :余弦相似度计算
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Spark笔记(1) :余弦相似度计算相关的知识,希望对你有一定的参考价值。
参考技术A spark在推荐系统中,基于物品的协同过滤算法是业界应用最多的算法,它的思想是给用户推荐那些和他们喜欢的物品相似的物品,主要分为两个步骤:一,计算物品之间的相似度;二,根据物品相似度和用户的历史行为给用户生成推荐列表。
其中物品的相似度的计算,可以通过余弦相似度计算。余弦相似度用向量空间中两个向量夹角的余弦值作为衡量两个个体间差异的大小。余弦值越接近1,就表明夹角越接近0度,也就是两个向量越相似,这就叫"余弦相似性"。
计算公式如下:
以文本相似度为例,用上述理论计算文本的相似性。
怎样计算上面两句话的相似程度?
基本思路是:如果这两句话的用词越相似,它们的内容就应该越相似。因此,可以从词频入手,计算它们的相似程度。
第一步,分词
第二步,列出所有的词
第三步,计算词频
第四步,写出词频向量
问题就变成了如何计算这两个向量的相似程度。可以想象成空间中的两条线段,都是从原点出发,指向不同的方向。两条线段之间形成一个夹角,如果夹角为0度,意味着方向相同、线段重合,这是表示两个向量代表的文本完全相等;如果夹角为180度,意味着方向正好相反。因此,我们可以通过夹角的大小,来判断向量的相似程度。夹角越小,就代表越相似。
使用上面的公式计算可得:
计算结果中夹角的余弦值为0.81非常接近于1,所以,上面的句子A和句子B是基本相似的。
spark例子:
运行结果:
计算两个向量的余弦相似度
文章目录
摘要
余弦相似度是判断两个向量相似度常用的算法,我在做行人重识别的时候,用到了余弦相似度的算法,记录一下。
基本概念
余弦相似度算法:一个向量空间中两个向量夹角间的余弦值作为衡量两个个体之间差异的大小,余弦值接近1,夹角趋于0,表明两个向量越相似,余弦值接近于0,夹角趋于90度,表明两个向量越不相似。
总之,相似度越小,距离越大。相似度越大,距离越小。
数学原理
所以余弦的计算公式如下:
cos
θ
=
a
2
+
b
2
−
c
2
2
a
b
\\cos \\theta=\\fraca^2+b^2-c^22 a b
cosθ=2aba2+b2−c2
a,b,c 是三个边的长度。
在直角坐标系中,向量表示的三角形的余弦函数是怎么样的呢?下图中向量a用坐标(x1,y1)表示,向量b用坐标(x2,y2)表示。
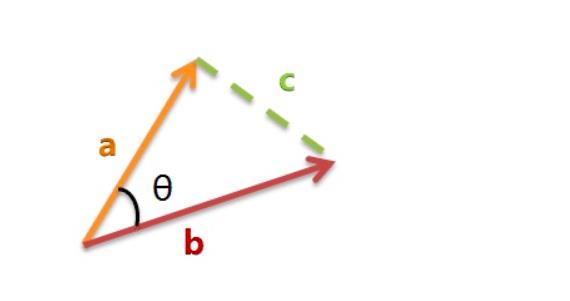
向量
a
\\mathrma
a 和向量
b
\\mathrmb
b 在直角坐标中的长度为
c
=
x
1
2
+
y
1
2
c=\\sqrtx_1^2+y_1^2
c=x12+y12,
b
=
x
2
2
+
y
2
2
b=\\sqrtx_2^2+y_2^2
b=x22+y22 , 向量
a
\\mathrma
a 和向量
b
\\mathrmb
b 之间的距离我们用向量
c
\\mathrmc
c 表示,就是上图中的黄色直线,那么向 量 c 在直角坐标系中的长度为
c
=
(
x
2
−
x
1
)
2
+
(
y
2
−
y
1
)
2
\\mathrmc=\\sqrt\\left(x_2-x_1\\right)^2+\\left(y_2-y_1\\right)^2
c=(x2−x1)2+(y2−y1)2 , 将 a , b , c 带入三角函数的公式中得到如下的公式:
cos
(
θ
)
=
a
2
+
b
2
−
c
2
2
a
b
=
x
1
2
+
y
1
2
+
x
2
2
+
y
2
2
−
(
x
2
−
x
1
)
2
−
(
y
2
−
y
1
)
2
2
x
1
2
+
y
1
2
∗
x
2
2
+
y
2
2
=
x
1
∗
x
2
+
y
1
∗
y
2
x
1
2
+
y
1
2
∗
x
2
2
+
y
2
2
\\beginarrayl \\cos (\\theta)=\\fraca^2+b^2-c^22 a b=\\fracx_1^2+y_1^2+x_2^2+y_2^2-\\left(x_2-x_1\\right)^2-\\left(y_2-y_1\\right)^22 \\sqrtx_1^2+y_1^2 * \\sqrtx_2^2+y_2^2 \\\\ =\\fracx_1 * x_2+y_1 * y_2\\sqrtx_1^2+y_1^2 * \\sqrtx_2^2+y_2^2 \\endarray
cos(θ)=2aba2+b2−c2=2x12+y12∗x22+y22x12+y12+x22+y22−(x2−x1)2−(y2−y1)2=x12+y12∗x22+y22x1∗x2+y1∗y2

在多维向量中,余弦的这种计算方法也成立。假定 A 和 B 是两个 n 维向量, A 是
[
A
1
,
A
2
,
…
,
A
n
]
[A 1 , A 2 , \\ldots, A n]
[A1,A2,…,An] , B 是
[
B
1
,
B
2
,
.
.
,
B
n
]
[B 1 , B 2 ,.., B n]
[B1,B2,..,Bn] , 则 A 与的夹角 \\theta 的余弦等于:
cos
θ
=
∑
i
=
1
n
(
A
i
×
B
i
)
∑
i
=
1
n
(
A
i
)
2
×
∑
i
=
1
n
(
B
i
)
2
=
A
⋅
B
∣
A
∣
×
∣
B
∣
\\beginaligned \\cos \\theta & =\\frac\\sum_i=1^n\\left(A_i \\times B_i\\right)\\sqrt\\sum_i=1^n\\left(A_i\\right)^2 \\times \\sqrt\\sum_i=1^n\\left(B_i\\right)^2 \\\\ & =\\fracA \\cdot B|A| \\times|B| \\endaligned
cosθ余弦计算相似度理解以及计算