浅谈splay（点的操作）

Posted 2020-08-31 日拱一卒 功不唐捐

                                             浅谈splay（点的操作）

一、基本概念

splay本质：二叉查找树

特点：结点x的左子树权值都小于x的权值，右子树权值都大于x的权值

维护信息：

  整棵树：root 当前根节点  sz书上所有结点编号

  结点：f[] 父节点编号    ch[][2] 孩子结点编号，0左1右  

          siz[] 以结点为根的子树大小（包括自己）   cnt[]自己出现的次数

          key[] 结点权值

二、基本操作

插入insert、删除del、查询x的排名findpos、查询排名为x的数findx、查找前驱pre、查找后继nex     

核心操作：伸展操作splay

part 1：这么多操作难免会更改节点信息，我们先思考如何维护这些信息

          siz，cnt 可以这样维护

void update(int x)
{
    siz[x]=cnt[x];
    if(ch[x][0]) siz[x]+=siz[ch[x][0]];
    if(ch[x][1]) siz[x]+=siz[ch[x][1]];
}

         f，ch，root 要在splay操作中修改

splay操作：就是讲结点x不断旋转至根节点

旋转过程谁成为谁的左右孩子，自己根据大小关系判断总结即可

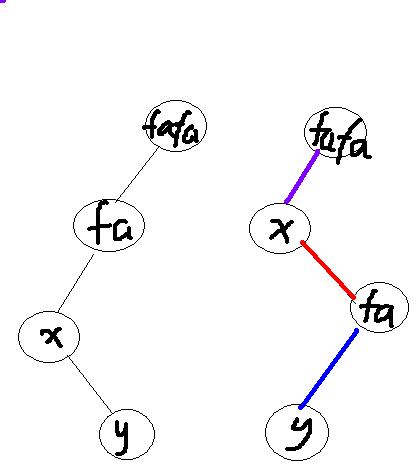
旋转代码：

int getson(int x) 
{
    return ch[f[x]][1]==x;
}
void rotate(int x)
{
    int fa=f[x],fafa=f[fa],k=getson(x);
    ch[fa][k]=ch[x][k^1];f[ch[fa][k]]=fa;//对应蓝色线，调整x另一方向的孩子和x父节点的关系 
    ch[x][k^1]=fa;f[fa]=x;//对应红色线 ，调整x和父节点的关系
    f[x]=fafa;
    if(fafa) ch[fafa][ch[fafa][1]==fa]=x;//对应紫色线 ，调整x和父节点的父节点的关系
    update(fa);update(x);
}

小细节：为什么先update(fa),再update（x） ，因为旋转前，fa是x的父节点，经旋转后，fa变为x的孩子节点，update操作是根据左右孩子子树大小更新的

调用：（双旋） 个人对于双旋的一点理解：http://www.cnblogs.com/TheRoadToTheGold/p/6372344.html

void splay(int x)
{
    for(int fa;fa=f[x];rotate(x))
     if(f[fa]) rotate(getson(x)==getson(fa) ? fa :x);
    root=x; 
}

小细节：fa=f[x]，1、每执行一次旋转，更新一次da   2、fa==true时才进行

part 2：

A、插入数x  insert（int x）

    分为3种情况

        1、树为空，直接插入x，并让x成为根节点

        2、树不为空  ①树中已有x，x出现次数+1，以x为根的子树大小+1，旋转x至根节点

                          ②树中没有x，在适当位置插入x，旋转x至根节点 

void create(int x)
{
    sz++;key[sz]=x;
    cnt[sz]=siz[sz]=1;
    ch[sz][0]=ch[sz][1]=f[sz]=0;
}
void insert(int x)//插入结点x 
{
    if(!root) create(x),root=sz;//splay为空
    else
    {
        int now=root,fa=0;
        while(1)
        {
            if(key[now]==x)//树中有x 
            {
                cnt[now]++;
　　　　　　　　　 siz[now]++;
                splay(now);
                break;
            }
            fa=now;
            now=ch[fa][x>key[fa]];
            if(!now)
            {
                create(x);
                f[sz]=fa;
                ch[fa][x>key[fa]]=sz;
                splay(sz);
                break;
            }
        }
    }
}

小细节：为什么要splay？仅仅是插入不是插进去就行吗？成不成为根节点有什么关系？

这是为了查找比x小/大的第一个数做铺垫，因为有可能x在树中没有出现过，所以先插入x，再找前驱/后继，这就可以直接从根节点找起，不用再找一次x的位置，最后删除x

（下面的E、F）

B、查询排名为x的数（从小到大）

记得平衡树怎么查找第k小吗？——如果左子树大小<k，找左孩子，否则找右孩子。

类比一下可以得出

1、如果x<当前点左子树大小，找左孩子，这里注意一个小细节是要先判断当前点是否有左孩子

2、否则  定义变量temp=当前结点出现次数+结点左子树大小

       ①、如果x<=temp 那么这个结点就是答案

因为既然x>=当前点左子树大小，那么他要么是当前点，要么在当前点的右子树

又因为x<=当前点+左子树大小+当前点出现次数，那么他是当前点

       ②、如果x>temp 那么x减去temp，找右孩子

int findx(int x)
{
    int now=root;
    while(1)
    {
        if(ch[now][0]&&x<=siz[ch[now][0]]) now=ch[now][0];//千万不要漏了ch[now][0]==true 
        else
        {
            int temp=(ch[now][0] ? siz[ch[now][0]] : 0)+cnt[now];
            if(x<=temp) return key[now];
            x-=temp;
            now=ch[now][1];
        }
    }
}

C、查询x的排名

想想splay本质是二叉查找树，不难得出

1、如果x<当前节点权值  查找左孩子

2、否则 ，先令ans加上当前节点左子树大小

    ①、如果x=当前节点权值，旋转当前节点至根节点，返回ans+1 

因为此时ans不包括当前节点，所以要+1

    ②、如果x>当前节点权值，ans加上当前节点出现次数，查找右孩子

int findpos(int x)
{
    int now=root,ans=0;
    while(1)
    {
        if(x<key[now]) now=ch[now][0];
        else
        {
            ans+=ch[now][0] ? siz[ch[now][0]] : 0; 
            if(x==key[now])
            {
                splay(now);
                return ans+1;
            }
            ans+=cnt[now];
            now=ch[now][1];
        }
    }
}

小细节：为什么要splay？

为了下面的删除操作做铺垫，删除数x需要先找到x的位置，删除操作是在x是根节点的基础上进行的（下面的F）

D、查找比x小的第一个数

这就有2种可能：x在树中，x不在树中

x在树中就是查找x的前驱，那么不在树中呢?

我们可以向在树中插入x，在查找前驱，最后再删除x

如何查找前驱? 转向x的左孩子l，然后在l的子树里一直往右找

调用代码：

insert(x);printf("%d\\n",key[pre()]);del(x);break;

查找前驱代码：

int pre()
{
    int now=ch[root][0];
    while(ch[now][1]) now=ch[now][1];
    return now;
}

E、查询比x大的第一个数

同理D

直接给代码

insert(x);printf("%d\\n",key[nex()]);del(x);break;

int nex()
{
    int now=ch[root][1];
    while(ch[now][0]) now=ch[now][0];
    return now;
}

F、删除数x

分为5种情况

首先，你要先找到x在哪儿，将其旋转至根节点，这里可以直接调用findpos函数

然后，分类讨论（此时根节点就是数x，所以此后操作变为删除根节点）

删除：结点所有信息清0即可

void clear(int x)
{
    ch[x][0]=ch[x][1]=cnt[x]=siz[x]=f[x]=key[x]=0;
}

1、根节点在splay树中出现次数>1  根节点的出现次数-1，子树大小-1

if(cnt[root]>1) 
    {
        cnt[root]--;siz[root]--;
        return;
    }

2、否则 ①  根节点既没有左孩子又没有右孩子，说明树中只有这一个结点，直接删去，并 root=0

if(!ch[root][0]&&!ch[root][1])
    {
        clear(root);
        root=0;//千万不要漏了这一句 
        return;
    }

          ② 根节点没有左孩子，说明树左边为空，那么只需把根节点的右孩子提为根节点，删除原根节点  小细节：新根节点的父节点置为0

    if(!ch[root][0])
    {
        int tmp=root;
        root=ch[root][1];
        f[root]=0;//不要漏了它 
        clear(tmp);
        return;
    }

        ③ 根节点没有右孩子，与②同理

 if(!ch[root][1])
    {
        int tmp=root;
        root=ch[root][0];
        f[root]=0;
        clear(tmp);
        return; 
    }

      ④ 根节点既有左孩子又有右孩子

我们可以先把x的前驱l旋转为根节点

手动模拟一下过程可以发现：

在l成为根节点的前一步，一定是x的左孩子 ，这说明了l成为根节点后，x不会有左孩子

那么我们就可以直接把x的右孩子提到x的位置，删除x即可

int pre1=pre(),tmp=root;//tmp现在相当于x的位置 
    splay(pre1);//x前驱旋转为根节点 ，经过此操作后，根节点变为x的前驱 
    ch[root][1]=ch[tmp][1];//x的右孩子提到x的位置 
    f[ch[tmp][1]]=root;//更新父节点 
    clear(tmp);//删除x 
    update(root);

为什么要在x是根节点的基础上执行删除操作？

因为splay要维护cnt、siz等信息

如果x不是根节点，x删除，x以上所有结点关于个数之类的信息都要更改

而如果x是根节点，x删除，不会影响其他结点

splay  插入insert、删除del、查询x的排名findpos、查询排名为x的数findx、查找前驱pre（第一个比x小的数）、查找后继nex（第一个比x大的数）完整代码

题目描述

您需要写一种数据结构（可参考题目标题），来维护一些数，其中需要提供以下操作：

1.插入x数

2.删除x数(若有多个相同的数，因只删除一个)

3.查询x数的排名(若有多个相同的数，因输出最小的排名)

4.查询排名为x的数

5.求x的前驱(前驱定义为小于x，且最大的数)

6.求x的后继(后继定义为大于x，且最小的数)

输入输出格式

输入格式：
第一行为n，表示操作的个数,下面n行每行有两个数opt和x，opt表示操作的序号(1<=opt<=6)

输出格式：
对于操作3,4,5,6每行输出一个数，表示对应答案

代码背景简述

题目来源：https://www.luogu.org/problem/show?pid=3369

#include<cstdio>
#define N 1000000
using namespace std;
int f[N],ch[N][2],key[N],cnt[N],siz[N],sz,root;
void update(int x)
{
    siz[x]=cnt[x];
    if(ch[x][0]) siz[x]+=siz[ch[x][0]];
    if(ch[x][1]) siz[x]+=siz[ch[x][1]];
}

int pre()
{
    int now=ch[root][0];
    while(ch[now][1]) now=ch[now][1];
    return now;
}
int nex()
{
    int now=ch[root][1];
    while(ch[now][0]) now=ch[now][0];
    return now;
}
int getson(int x) 
{
    return ch[f[x]][1]==x;
}
void rotate(int x)
{
    int fa=f[x],fafa=f[fa],k=getson(x);
    ch[fa][k]=ch[x][k^1];f[ch[fa][k]]=fa;
    ch[x][k^1]=fa;f[fa]=x;
    f[x]=fafa;
    if(fafa) ch[fafa][ch[fafa][1]==fa]=x; 
    update(fa);update(x);
}
void splay(int x)
{
    for(int fa;fa=f[x];rotate(x))
     if(f[fa]) rotate(getson(x)==getson(fa) ? fa :x);
    root=x; 
}
int findpos(int x)
{
    int now=root,ans=0;
    while(1)
    {
        if(x<key[now]) now=ch[now][0];
        else
        {
            ans+=ch[now][0] ? siz[ch[now][0]] : 0; 
            if(x==key[now])
            {
                splay(now);
                return ans+1;
            }
            ans+=cnt[now];
            now=ch[now][1];
        }
    }
}
int findx(int x)
{
    int now=root;
    while(1)
    {
        if(ch[now][0]&&x<=siz[ch[now][0]]) now=ch[now][0];//千万不要漏了ch[now][0]==true 
        else
        {
            int temp=(ch[now][0] ? siz[ch[now][0]] : 0)+cnt[now];
            if(x<=temp) return key[now];
            x-=temp;
            now=ch[now][1];
        }
    }
}
void clear(int x)
{
    ch[x][0]=ch[x][1]=cnt[x]=siz[x]=f[x]=key[x]=0;
}
void create(int x)
{
    sz++;key[sz]=x;
    cnt[sz]=siz[sz]=1;
    ch[sz][0]=ch[sz][1]=f[sz]=0;
}
void insert(int x)
{
    if(!root) create(x),root=sz;
    else
    {
        int now=root,fa=0;
        while(1)
        {
            if(key[now]==x)
            {
                cnt[now]++;
               siz[now]++;
                splay(now);
                break;
            }
            fa=now;
            now=ch[fa][x>key[fa]];
            if(!now)
            {
                create(x);
                f[sz]=fa;
                ch[fa][x>key[fa]]=sz;
                splay(sz);
                break;
            }
        }
    }
}

void del(int x)
{
    int t=findpos(x);
    if(cnt[root]>1) 
    {
        cnt[root]--;siz[root]--;
        return;
    }
    if(!ch[root][0]&&!ch[root][1])
    {
        clear(root);
        root=0;
        return;
    }
    if(!ch[root][0])
    {
        int tmp=root;
        root=ch[root][1];
        f[root]=0;
        clear(tmp);
        return;
    }
    if(!ch[root][1])
    {
        int tmp=root;
        root=ch[root][0];
        f[root]=0;
        clear(tmp);
        return; 
    }
    int pre1=pre(),tmp=root;
    splay(pre1);
    ch[root][1]=ch[tmp][1];
    f[ch[tmp][1]]=root;
    clear(tmp);
    update(root);
}
int main()
{
    int n,opt,x;
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%d%d",&opt,&x);
        switch(opt)
        {
            case 1 :insert(x);break; //插入x 
            case 2 :del(x);break;//删除x 
            case 3 :printf("%d\\n",findpos(x));break;//查询x的排名 
            case 4 :printf("%d\\n",findx(x));break;//查询排名为x的数 
            case 5 :insert(x);printf("%d\\n",key[pre()]);del(x);break;//查找第一个小于x的数 
            case 6 :insert(x);printf("%d\\n",key[nex()]);del(x);break;//查找第一个大于x的数 
        }
    }
}

View Code