Splay和LCT的复杂度分析

Posted 2021-01-25 reverymoon

(Splay)的复杂度分析

不论插入，删除还是访问，我们可以发现它们的复杂度都和(splay)操作的复杂度同阶，只是一点常数的区别

我们不妨假设有(n)个点的(splay)，进行了(m)次(splay)操作

---

采用势能分析

我们记(w(x) = left lceil log_2 (size(x)) ight ceil)，注意以(2)为底和上取整

我们定义势能函数为(varphi = sum w(x))

（记第(i)次操作操作完之后，势能为(varphi(i))）

只需要估计出(varphi(m) - varphi(m - 1) + varphi(m - 1) - varphi(m - 2) ... + varphi(1) - varphi(0) + varphi(0))的大小即可

（即初始势能和每次的势能变化量的和）

显然，(varphi(0) leqslant n log n)

---

(splay)操作的具体定义为：

如果父节点是根，那么旋转一次

如果父节点和爷节点所处子树方向一致，那么先旋转父亲再旋转自己

否则，旋转两次自己

实际上可以归结于(zig)，(zag)，(zig-zig)，(zag-zag)，(zig-zag)，(zag-zig)操作

由于(zig)和(zag)是对称的操作

因此，只需要对(zig)，(zig-zig)，(zig-zag)操作分析复杂度即可

---

(zig)操作

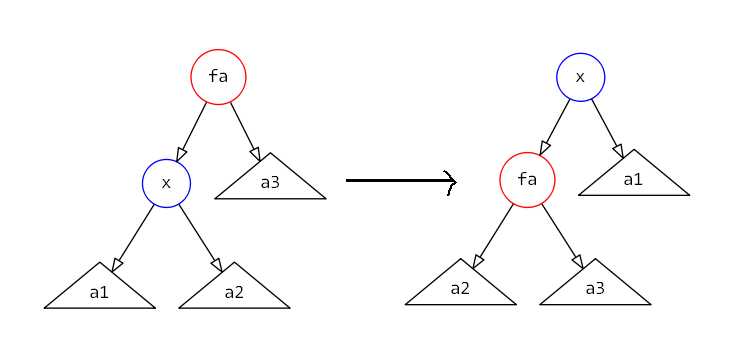
势能的变化量为(1 + w'(x) + w'(fa) - w(x) - w(fa) leq 1 + w'(fa) - w(x) leq 1 + w'(x) - w(x))

---

(zig-zig)操作

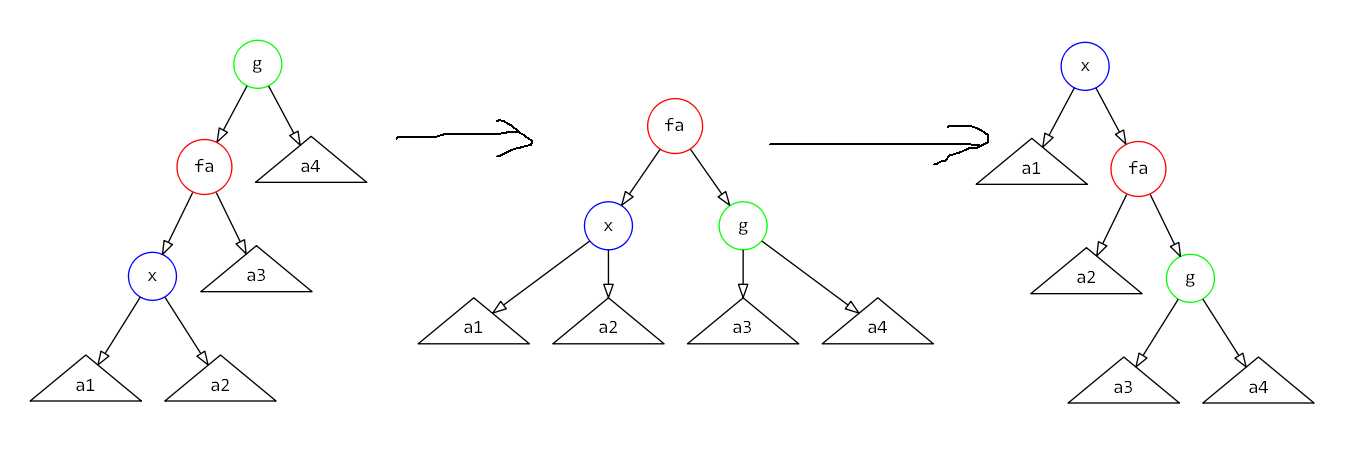
势能变化量为(1 + w'(x) + w'(fa) + w'(g) - w(x) - w(fa) - w(g))（缩小了常数的影响，但不能无视）

(leq 1 + w'(fa) + w'(g) - w(x) - w(fa) leq 1 + w'(x) + w'(g) - 2w(x))

这是神仙复杂度证明中非常神奇的地方，通过一些有趣的性质，让常数项的代价合并到了势能的变化中

我们不妨设(a = w'(g), b = w(x))，那么注意到(w'(x) = a + b + 1)

由于$2w‘(x) - w‘(g) - w(x) = left lceil log_2 (a + b + 1) ight ceil - left lceil log_2 a ight ceil + left lceil log_2 a + b + 1 ight ceil - left lceil log_2 b ight ceil $

注意到(a, b)在上式中是对称的，不妨设(a geq b)

(geq left lceil log_2 (a + b + 1) ight ceil - left lceil log_2 b ight ceil geq left lceil log_2 (2b + 1) ight ceil - left lceil log_2 b ight ceil geq left lceil log_2 b ight ceil + 1 - left lceil log_2 b ight ceil geq 1)

因此有(1 leq 2w'(x) - w'(g) - w(x))，我们将(1 + w'(x) + w'(g) - 2w(x))中的(1)放缩，可以得到

(leq 3(w'(x) - w(x)))

---

(zig-zag)操作

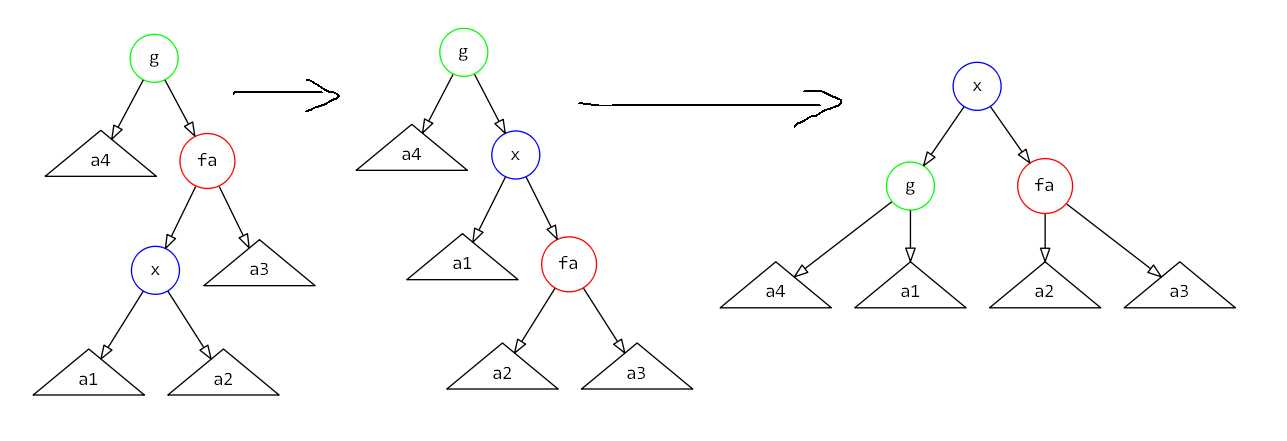
势能变化量为(1 + w'(x) + w'(fa) + w'(g) - w(x) - w(fa) - w(g) leq 1 + w'(fa) + w'(g) - w(x) - w(fa) leq 1 + w'(g) + w'(fa) - 2w(x))

由上文的结论，我们知道这里可以把(1)放缩成(1 leq 2w'(x) - w'(g) - w'(fa))

因此(leq 2(w'(x) - w(x)))

---

把以上三种操作的势能全部放缩为(leq 3(w'(x) - w(x)))

不妨假设(splay)一次，依次访问了点(x_1, x_2 ... x_n)，最后(x_1)会成为新的根

那么，最后的势能实际上是(3(w'(x_1) - w(x_1) + w''(x_1) - w'(x_1) + .... + w(n) - w^{'''.....}(x_1)) + 1 = 3 * (w(n) - w(x_1)) + 1leq log_2 n)

因此，(varphi(m) - varphi(m - 1) + varphi(m - 1) - varphi(m - 2) ... + varphi(1) - varphi(0) + varphi(0) = n log n + m log n)

即(n)个点的(splay)，做(m)次(splay)操作，复杂度为(O(n log n + m log n))

---

(LCT)的复杂度分析

先让我咕一会