D 洛谷 P3602 Koishi Loves Segments [贪心 树状数组+堆]

Posted 2020-08-29 Candy?

题目描述

Koishi喜欢线段。

她的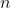条线段都能表示成数轴上的某个闭区间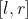。Koishi喜欢在把所有线段都放在数轴上，然后数出某些点被多少线段覆盖了。

Flandre看她和线段玩得很起开心，就抛给她一个问题：

数轴上有个点突然兴奋，如果自己被身上覆盖了超过条线段，这个点就会浑身难受然后把Koishi批判一番。

Koishi十分善良，为了不让数轴上的点浑身难受，也为了让自己开心，她想在数轴上放入尽量多的线段。

按照套路，Koishi假装自己并不会做这道题，所以她就来求你帮忙。并承诺如果你解决了问题就给你打一通电话w。

输入输出格式

输入格式：

 

第一行两个个整数，分别表示插入的线段数和关键点数。

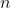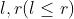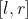接下来行，每行两个整数，表示线段的端点。

接下来行，每行两个整数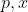，表示有个位于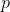的点突然兴奋，并认为自己身上不得覆盖超过条线段

 

输出格式：

 

一个整数，表示最多能放入的线段数

 

输入输出样例

输入样例#1：

4 3
1 3
2 4
5 7
6 8
2 5
3 1
6 2

输出样例#1：

3

说明

对于20%的数据，满足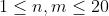

对于60%的数据，满足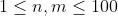

对于80%的数据，满足

对于100%的数据，满足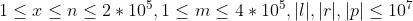

如果一个点兴奋了两次，那么Koishi应当满足它的*较严苛的要求*（也就是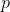相同时取最小值啦）

请适当使用读入优化

---

 

比赛时交了一个网络流60分

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
typedef long long ll;
const int N=1005,M=1e6,INF=1e9;
inline int read(){
    char c=getchar();int x=0,f=1;
    while(c<\'0\'||c>\'9\'){if(c==\'-\')f=-1; c=getchar();}
    while(c>=\'0\'&&c<=\'9\'){x=x*10+c-\'0\'; c=getchar();}
    return x*f;
}
int n,m,s,t;
struct rec{
    int l,r;
}a[N];
struct point{
    int p,k;
    bool operator <(const point a)const{
        if(p==a.p) return k<a.k;
        else return p<a.p;
    }
}b[N];

struct edge{
    int v,c,f,ne;
}e[M<<1];
int cnt,h[N];
inline void ins(int u,int v,int c){
    cnt++;
    e[cnt].v=v;e[cnt].c=c;e[cnt].f=0;e[cnt].ne=h[u];h[u]=cnt;
    cnt++;
    e[cnt].v=u;e[cnt].c=0;e[cnt].f=0;e[cnt].ne=h[v];h[v]=cnt;
}
int cur[N],d[N],vis[N];
int q[N],head,tail;
bool bfs(){
    head=tail=1;
    memset(vis,0,sizeof(vis));
    d[s]=1;vis[s]=1;q[tail++]=s;
    while(head!=tail){
        int u=q[head++];
        for(int i=h[u];i;i=e[i].ne){
            int v=e[i].v;
            if(!vis[v]&&e[i].c>e[i].f){
                vis[v]=1;d[v]=d[u]+1;
                q[tail++]=v;
                if(v==t) return true;
            }
        }
    }
    return false;
}
int dfs(int u,int a){
    if(u==t||a==0) return a;
    int flow=0,f;
    for(int &i=cur[u];i;i=e[i].ne){
        int v=e[i].v;
        if(d[v]==d[u]+1&&(f=dfs(v,min(e[i].c-e[i].f,a)))>0){
            flow+=f;
            e[i].f+=f;
            e[((i-1)^1)+1].f-=f;
            a-=f;
            if(a==0) break;
        }
    }
    if(a) d[u]=-1;
    return flow;
}
int dinic(){
    int flow=0;
    while(bfs()){
        for(int i=s;i<=t;i++) cur[i]=h[i];
        flow+=dfs(s,INF);
    }
    return flow;
}
//int Bin(int v){
//    int l=1,r=m;
//    while(l<r){
//        int mid=(l+r)>>1;
//        if(v<=b[mid].p) r=mid;
//        else if(v>b[mid].p) l=mid+1;
//    }
//    return l;
//}


void buildGraph(){
    for(int i=1;i<=m;i++) ins(n+n+i,n+n+m+i,b[i].k);
    for(int i=1;i<=n;i++){
        ins(s,i,1);ins(n+i,t,1);
        int now=i;
        for(int j=1;j<=m;j++){
            if(b[j].p<a[i].l) continue;
            if(b[j].p>a[i].r) break;
            ins(now,n+n+j,1);
            now=n+n+m+j;
        }
        ins(now,n+i,1);
    }
}
void getMP(){
    sort(b+1,b+1+n);
    int p=0;b[++p]=b[1];
    for(int i=2;i<=m;i++)
        if(b[i].p!=b[i-1].p) b[++p]=b[i];
    m=p;
}
int main(int argc, const char * argv[]){
    n=read();m=read();
    for(int i=1;i<=n;i++) a[i].l=read(),a[i].r=read();
    for(int i=1;i<=m;i++) b[i].p=read(),b[i].k=read();
    getMP();s=0;t=n+n+m+m+1;
    buildGraph();
    printf("%d",dinic());
    return 0;
}

网络流

正解是贪心 从左到右考虑每一个点和线段 这个点不满足条件就删除覆盖它的且r最大的线段

实现起来有好多做法，标程用了set维护覆盖当前考虑点的所有线段

好多人用了线段树(和矩形面积并类似)，然而并不明白它们怎么找的线段

其实加减线段 询问一个点覆盖次数直接差分后用树状数组就好了.....然后用一个堆维护当前加入的所有线段为了取出r最大的线段

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <queue>
using namespace std;
typedef long long ll;
const int N=4e5+5,M=1e6+5;
inline int read(){
    char c=getchar();int x=0,f=1;
    while(c<\'0\'||c>\'9\'){if(c==\'-\')f=-1; c=getchar();}
    while(c>=\'0\'&&c<=\'9\'){x=x*10+c-\'0\'; c=getchar();}
    return x*f;
}
int n,m;
int mp[M];
void iniMP(){
    sort(mp+1,mp+1+mp[0]);
    int p=0;
    mp[++p]=mp[1];
    for(int i=2;i<=mp[0];i++) if(mp[i]!=mp[i-1]) mp[++p]=mp[i];
    mp[0]=p;
}
inline int Bin(int v){
    int l=1,r=mp[0];
    while(l<=r){
        int mid=(l+r)>>1;
        if(v==mp[mid]) return mid;
        else if(v<mp[mid]) r=mid-1;
        else l=mid+1;
    }
    return 0;
}

int c[M];
inline int lowbit(int x){return x&-x;}
inline void add(int p,int v){for(;p<=mp[0];p+=lowbit(p)) c[p]+=v;}
inline int sum(int p){
    int re=0;
    for(;p>0;p-=lowbit(p)) re+=c[p];
    return re;
}
struct Segment{
    int l,r;
    bool operator <(const Segment &a)const{return l<a.l;}
}s[N];
struct Point{
    int p,x;
    bool operator <(const Point &a)const{return p<a.p;}
}a[N];
struct Node{
    int r,id;
    bool operator <(const Node &a)const{return r<a.r;}
    Node(int a=0,int b=0):r(a),id(b){}
};
priority_queue<Node> q;
int ans;
void solve(){
    for(int i=1;i<=n;i++) s[i].l=Bin(s[i].l),s[i].r=Bin(s[i].r);
    for(int i=1;i<=m;i++) a[i].p=Bin(a[i].p);
    sort(s+1,s+1+n);
    sort(a+1,a+1+m);
    for(int i=1,j=1;i<=m;i++){
        for(;j<=n&&s[j].l<=a[i].p;j++){
            add(s[j].l,1);
            add(s[j].r,-1);
            q.push(Node(s[j].r,j));ans++;
        }
        while(sum(a[i].p)>a[i].x){
            int x=q.top().id; q.pop();ans--;
            add(s[x].l,-1);
            add(s[x].r,1);
        }
    }
    printf("%d",ans);
}
int main(int argc, const char * argv[]){
    n=read();m=read();
    for(int i=1;i<=n;i++)
        mp[++mp[0]]=s[i].l=read(),mp[++mp[0]]=s[i].r=read()+1;
    
    for(int i=1;i<=m;i++)
        mp[++mp[0]]=a[i].p=read(),a[i].x=read();
    iniMP();
    solve();
    return 0;
}