树链剖分简(单)介(绍)
Posted 阿波罗2003
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了树链剖分简(单)介(绍)相关的知识,希望对你有一定的参考价值。
树链剖分可以算是一种数据结构(一大堆数组,按照这个意思,主席树就是一大堆线段树)。将一棵树分割成许多条连续的树链,方便完成一下问题:
- 单点修改(dfs序可以完成)
- 求LCA(各种乱搞也可以)
- 树链修改(修改任意树上两点之间的唯一路径)
- 树链查询
- (各种操作)
前两个内容可以用其他方式解决,但是下面两种操作倍增、st表,dfs序就很难解决(解决当然可以解决,只是耗时长点而已)。下面开始步入正题。
树链剖分的主要目的是分割树,使它成一条链,然后交给其他数据结构(如线段树,Splay)来进行维护。常见的分割树的方法(轻重链剖分)就是分重儿子和轻儿子。对于一个根节点,它的节点最多的子树的根节点(也就是它的某个子节点,如果有几个数量相同,那么随意),其它都是轻儿子。根节点和重儿子连成的边叫重边,根节点和轻儿子连成的边叫轻边。如下图:

由此,由于这种剖分方式便有了一些性质:
| 一条根节点到叶节点的路径上,轻边的条数不超过log2n条 | 因为轻儿子的所在子树的节点总数不超过父节点的size的一半(不然它就成重儿子了),所以最多log2n条轻边后,节点总数就变为1了 |
| 一条根节点到叶节点的路径上,重链的条数不超过log2n条 | |
| 有2log22n条重链精确覆盖树上任意两点之间的路径 |
重边相连的点构成了重链(特殊的,单独的一个点,比如说4、9、11号节点也可以看成是重链),然后为了能够让其它数据结构能够更好地处理这棵树,就为这棵树重新编号,让一条重链上的所有点的编号是连续的(这样才能快速查询,修改)。于是改变了dfs的顺序,先访问重儿子,再访问其它儿子,于是由上图得到了下面这个序列:

于是单点修改的时候,直接交给线段树处理掉就行了。下面来解决求LCA的问题,比如说节点8和节点4。首先将树链开始深度更深的一个节点跳到树链的开头,再往上跳到父节点(新的一个树链),直到两个点到了同一条重链上,返回深度更小的那个点,就是LCA。
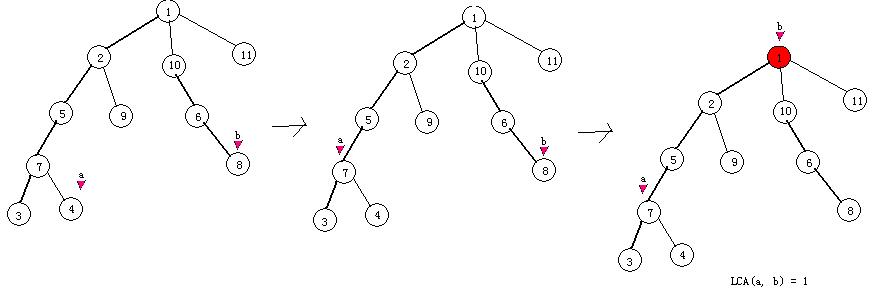
代码还挺短的:
1 int lca(int a, int b){ 2 while(top[a] != top[b]){ 3 int& d = (dep[top[a]] > dep[top[b]]) ? (a) : (b); 4 d = fa[top[d]]; 5 } 6 return (dep[a] < dep[b]) ? (a) : (b); 7 }
对于链上修改,链上查询的思路差不多,只不过在从一个点跳到另一个点上,要用线段树得到这一段路径的值,由于这条路径上的重链数量不超过$\\log_2 n$,所以时间复杂度为$O(\\log ^2 n)$。(还算能够接受)
根据以上各种操作,得出了以下需要预处理出的数组:
size[i]:节点i的大小(以节点i为根的子树的节点总数)
zson[i]:节点i的重儿子(如果没有,就用个特值表示好了,以便区分)
dep[i]:节点i的深度
fa[i]:节点i的父节点
top[i]:节点i所在的重链的dep最小的一个节点
visitID[i]:节点i的访问编号
exitID[i]:节点i的离开时编号(如果没有对整棵子树进行操作的操作就可以不用)
visit[i]:第i个访问的节点是(建立线段树的时候使用)
前四个可以第一次dfs搞定:
1 void dfs1(int node, int last) { 2 dep[node] = dep[last] + 1; 3 size[node] = 1; 4 fa[node] = last; 5 int maxs = 0, maxid = 0; 6 for(int i = m_begin(g, node); i != 0; i = g[i].next) { 7 int& e = g[i].end; 8 if(e == last) continue; 9 dfs1(e, node); 10 size[node] += size[e]; 11 if(size[e] > maxs) maxs = size[e], maxid = e; 12 } 13 zson[node] = maxid; 14 }
后四个不着急,不忙一次搞完,第二次dfs,把剩下的这四个数组的值都get到。
1 void dfs2(int node, int last, boolean iszson) { 2 top[node] = (iszson) ? (top[last]) : (node); 3 visitID[node] = ++cnt; 4 visit[cnt] = node; 5 if(zson[node] != 0) dfs2(zson[node], node, true); 6 for(int i = m_begin(g, node); i != 0; i = g[i].next) { 7 int& e = g[i].end; 8 if(e == last || e == zson[node]) continue; 9 dfs2(e, node, false); 10 } 11 exitID[node] = cnt; 12 }
bzoj1036的完整代码(可能和上面有点出入):
1 /** 2 * bzoj 3 * Problem#1036 4 * Accepted 5 * Time:2464ms 6 * Memory:6060k 7 */ 8 #include<iostream> 9 #include<fstream> 10 #include<sstream> 11 #include<cstdio> 12 #include<cstdlib> 13 #include<cstring> 14 #include<ctime> 15 #include<cctype> 16 #include<cmath> 17 #include<algorithm> 18 #include<stack> 19 #include<queue> 20 #include<set> 21 #include<map> 22 #include<vector> 23 #ifndef WIN32 24 #define AUTO "%lld" 25 #else 26 #define AUTO "%I64d" 27 #endif 28 using namespace std; 29 typedef bool boolean; 30 #define inf 0xfffffff 31 #define smin(a, b) (a) = min((a), (b)) 32 #define smax(a, b) (a) = max((a), (b)) 33 template<typename T> 34 inline void readInteger(T& u){ 35 char x; 36 int aFlag = 1; 37 while(!isdigit((x = getchar())) && x != \'-\' && x != -1); 38 if(x == -1) return; 39 if(x == \'-\'){ 40 x = getchar(); 41 aFlag = -1; 42 } 43 for(u = x - \'0\'; isdigit((x = getchar())); u = (u << 3) + (u << 1) + x - \'0\'); 44 ungetc(x, stdin); 45 u *= aFlag; 46 } 47 48 ///map template starts 49 typedef class Edge{ 50 public: 51 int end; 52 int next; 53 Edge(const int end = 0, const int next = 0):end(end), next(next){} 54 }Edge; 55 typedef class MapManager{ 56 public: 57 int ce; 58 int *h; 59 Edge *edge; 60 MapManager(){} 61 MapManager(int points, int limit):ce(0){ 62 h = new int[(const int)(points + 1)]; 63 edge = new Edge[(const int)(limit + 1)]; 64 memset(h, 0, sizeof(int) * (points + 1)); 65 } 66 inline void addEdge(int from, int end){ 67 edge[++ce] = Edge(end, h[from]); 68 h[from] = ce; 69 } 70 inline void addDoubleEdge(int from, int end){ 71 addEdge(from, end); 72 addEdge(end, from); 73 } 74 Edge& operator [](int pos) { 75 return edge[pos]; 76 } 77 }MapManager; 78 #define m_begin(g, i) (g).h[(i)] 79 ///map template ends 80 81 typedef class SegTreeNode { 82 public: 83 int maxv; 84 long long sum; 85 SegTreeNode* left, *right; 86 87 SegTreeNode():maxv(-inf), left(NULL), right(NULL) { } 88 89 inline void pushUp(){ 90 maxv = max(left->maxv, right->maxv); 91 sum = left->sum + right->sum; 92 } 93 }SegTreeNode; 94 95 typedef class SegTree { 96 public: 97 SegTreeNode* root; 98 SegTree():root(NULL){ } 99 SegTree(int size, int* list, int* keyer){ 100 build(root, 1, size, list, keyer); 101 } 102 103 void build(SegTreeNode*& node, int l, int r, int* list, int* keyer) { 104 node = new SegTreeNode(); 105 if(l == r) { 106 node->maxv = list[keyer[l]]; 107 node->sum = list[keyer[l]]; 108 return; 109 } 110 int mid = (l + r) >> 1; 111 build(node->left, l, mid, list, keyer); 112 build(node->right, mid + 1, r, list, keyer); 113 node->pushUp(); 114 } 115 116 void update(SegTreeNode*& node, int l, int r, int index, int val) { 117 if(l == index && r == index) { 118 node->maxv = val; 119 node->sum = val; 120 return; 121 } 122 int mid = (l + r) >> 1; 123 if(index <= mid) update(node->left, l, mid, index, val); 124 else update(node->right, mid + 1, r, index, val); 125 node->pushUp(); 126 } 127 128 int query_max(SegTreeNode*& node, int l, int r, int from, int end){ 129 if(l == from && r == end){ 130 return node->maxv; 131 } 132 int mid = (l + r) >> 1; 133 if(end <= mid) return query_max(node->left, l, mid, from, end); 134 if(from > mid) return query_max(node->right, mid + 1, r, from, end); 135 int a = query_max(node->left, l, mid, from, mid); 136 int b = query_max(node->right, mid + 1, r, mid + 1, end); 137 return max(a, b); 138 } 139 140 long long query_sum(SegTreeNode*& node, int l, int r, int from, int end){ 141 if(l == from && r == end){ 142 return node->sum; 143 } 144 int mid = (l + r) >> 1; 145 if(end <= mid) return query_sum(node->left, l, mid, from, end); 146 if(from > mid) return query_sum(node->right, mid + 1, r, from, end); 147 return query_sum(node->left, l, mid, from, mid) + query_sum(node->right, mid + 1, r, mid + 1, end);; 148 } 149 }SegTree; 150 151 int cid, clink; 152 int* starter; //重链的开始位置 153 //int* dep; //节点深度 154 int* id; //编号(一条重链上的编号是连续的) 155 int* visit; //记录访问顺序 156 int* size; //节点的大小 157 int* zson; //节点的重儿子编号 158 int* belong; //节点属于的重链的编号 159 int* linkdep; //重链的深度 160 int* fa; //节点的父节点 161 MapManager g; 162 SegTree st; 163 164 void dfs1(int node, int last) { 165 size[node] = 1; 166 int maxs = 0, maxid = 0; 167 for(int i = m_begin(g, node); i != 0; i = g[i].next) { 168 int& e = g[i].end; 169 if(e == last) continue; 170 dfs1(e, node); 171 if(size[e] > maxs) maxs = size[e], maxid = e; 172 size[node] += size[e]; 173 } 174 zson[node] = maxid; 175 } 176 177 void dfs2(int node, int last, boolean iszson){ 178 id[node] = ++cid; 179 visit[cid] = node; 180 belong[node] = (iszson) ? (belong[last]) : (++clink); 181 if(!iszson) starter[clink] = node, linkdep[belong[node]] = linkdep[belong[last]] + 1; 182 fa[node] = last; 183 if(zson[node] != 0) dfs2(zson[node], node, true); 184 for(int i = m_begin(g, node); i != 0; i = g[i].next) { 185 int& e = g[i].end; 186 if(e == last || e == zson[node]) continue; 187 dfs2(e, node, false); 188 } 189 } 190 191 int n, m; 192 int *v; 193 194 int lca_max(int a, int b) { 195 int maxv = -inf; 196 while(belong[a] != belong[b]){ 197 int& d = (linkdep[belong[a]] > linkdep[belong[b]]) ? (a) : (b); 198 int res = st.query_max(st.root, 1, n, id[starter[belong[d]]], id[d]); 199 d = fa[starter[belong[d]]], smax(maxv, res); 200 } 201 if(id[a] > id[b]) swap(a, b); 202 int res = st.query_max(st.root, 1, n, id[a], id[b]); 203 return max(res, maxv); 204 } 205 206 long long lca_sum(int a, int b) { 207 long long sum = 0; 208 while(belong[a] != belong[b]){ 209 int& d = (linkdep[belong[a]] > linkdep[belong[b]]) ? (a) : (b); 210 sum += st.query_sum(st.root, 1, n, id[starter[belong[d]]], id[d]); 211 d = fa[starter[belong[d]]]; 212 } 213 if(id[a] > id[b]) swap(a, b); 214 long long res = st.query_sum(st.root, 1, n, id[a], id[b]); 215 return res + sum; 216 } 217 218 inline void init() { 219 readInteger(n); 220 g = MapManager(n, 2 * n); 221 v = new int[(const int)(n + 1)]; 222 for(int i = 1, a, b; i < n; i++){ 223 readInteger(a); 224 readInteger(b); 225 g.addDoubleEdge(a, b); 226 } 227 for(int i = 1; i <= n; i++) readInteger(v[i]); 228 } 229 230 inline void init_tl() { 231 int logn = n; 232 starter = new int[(const int)(logn + 1)]; 233 id = new int[(const int)(n + 1)]; 234 visit = new int[(const int)(n + 1)]; 235 size = new int[(const int)(n + 1)]; 236 zson = new int[(const int)(n + 1)]; 237 belong = new int[(const int)(n + 1)]; 238 linkdep = new int[(const int)(logn + 1)]; 239 fa = new int[(const int)(n + 1)]; 240 belong[0] = 0; 241 linkdep[0] = 0; 242 cid = clink = 0; 243 dfs1(1, 0); 244 dfs2(1, 0, false); 245 st = SegTree(n, v, visit); 246 } 247 248 inline void solve() { 249 readInteger(m); 250 char cmd[10]; 251 int a, b; 252 while(m--) { 253 scanf("%s", cmd); 254 readInteger(a); 255 readInteger(b); 256 if(cmd[0] == \'C\'){ 257 v[a] = b; 258 st.update(st.root, 1, n, id[a], b); 259 }else{ 260 if(cmd[1] == \'M\'){ 261 int res = lca_max(a, b); 262 printf("%d\\n", res); 263 }else{ 264 long long res = lca_sum(a, b); 265 printf(AUTO"\\n", res); 266 } 267 } 268 } 269 } 270 271 int main() { 272 init(); 273 init_tl(); 274 solve(); 275 return 0; 276 }
以上是关于树链剖分简(单)介(绍)的主要内容,如果未能解决你的问题,请参考以下文章