Knuth-Morris-Pratt Algorithm

Posted 2020-08-28 copperface

KMP背景分析

---

普通算法（遍历），会遗忘所有之前比较过的信息，导致每一次移位，都要重新重头比较每一个字符。这将会导致 O(mn)的时间复杂度（m: 关键字符长度，n: 文本string的长度）

而KMP算法，则能够保证不去重复比较已经部分匹配的字符，比如序列“abcdabac”，如果“abcd”部分匹配了文本，而在接下来的“a”位置上不匹配，那么算法则会直接跳过4个位置，重新进行比较，而不是移位1个，从头进行比较。这样就能够保证时间复杂度为 O(n)。说通俗一些就是直接跳到公共前后缀的位置：

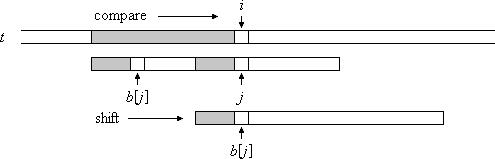
图中阴影部分代表公共前后缀，对于“abcdabac”就是“ab”

 

为了保证上述复杂度，需要对关键字符进行预处理（就是标明最长公共前后缀的辅助数组），而这一过程的时间复杂度为 O(m)。因为 m<n，所以总的算法时间复杂度为 O(n)

一些定义

---

令 x = abacab，那么x的一些术语描述如下：

proper prefixes 前缀:

   a, ab, aba, abac, abaca

proper suffixes 后缀:

   b, ab, cab, acab, bacab

borders 边界（前，后缀共有的最长子串）：

   ab

边界 ab 拥有 2 的宽度

而我们的预处理，就是对 关键字字符串 算出每个位置上的 边界。

比如：

j: 0 1 2 3 4 5

p[j]: a b a b a a

b[j]:   0 0 1 2 3 1

预处理过程

---

该过程就是生成 partial match table 或者称为 failure function的算法，即生成 b[j] 数组。

b[j]的生成过程，其实可以对关键字符串P，用 递推方式 算出来，时间复杂度为 O(m)

假设 b[0], ..., b[i-1] 已知，那么 边界b[i] 的值，通过比较 P_j，P_i 可以得到

如果P_j==P_i，那么如果当前 i-1 位置的边界宽度是j，那么 b[i] = j + 1

如果不相等，那么需要重新获得下一个最大边界长度，这里需要用到如下定理：

当字符串x的最大边界是s，次大边界是r，可以推得s的最大边界就是r。

当想扩展x的 边界s 不成功，那么就把x的边界变为s的边界r，重新扩展：

使用如下例子，关键子字符串P：

    j\'      j             i i\'

a a a b a a e e a a a b a a a ...

|r|                     |r|

|----s----|     |----s----|

|------------P------------|...

当前的位置i的最大边界是s，次大边界是r。假设边界s的宽度是 j = 6。

当i移动到下一个位置i\'的时候，“e”和“a”并不相等，边界无法拓展，于是更新 j = b[j-1], 于是j更新为r的宽度2，记为j\'

再次比较Pj\' 和 Pi\'是否相等，发现相等，于是更新b[i\'] = b[j\'] + 1;同时更新j\' = 3;(如果还不相等，就再次找r的最大边界，直到j更新为0）

代码

---

preprocessing的代码：

1 2 3 4 5 6 7 8 9 10 11 12 13

vector<int> kmpProcess(string s) {         vector<int> b(s.size(),0);         int j = 0;         //下面计算b[i]         for (int i = 1; i < s.size(); i++) {             while (j > 0 && s[i] != s[j])                  j = b[j - 1];//当前的widest border不满足要求，那么找到next widest border             if (s[i] == s[j])                  j++;             b[i] = j;         }         return b;     }

 

null