KMP(The Knuth-Morris-Pratt Algorithm)
Posted WhaleFall541
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了KMP(The Knuth-Morris-Pratt Algorithm)相关的知识,希望对你有一定的参考价值。
本文代码来自于中国大学MOOC
注释内容为自己理解,如有错误请评论,或者私信给我,谢谢
#include <stdio.h>
#include "stdlib.h"
#include "string.h"
typedef int Position;
Position KMP(char string[25], char pattern[7]);
void BuildMatch(char *pattern, int *pInt);
#define NotFound -1
int main() {
char string[] = "this is a simple example";
char pattern[] = "simple";
Position p = KMP(string, pattern);
if (p == NotFound) printf("Not found.\\n");
else {
printf("%s\\n", string + p);
printf("%f\\n", p);
}
return 0;
}
Position KMP(char *string, char *pattern) {
int n = strlen(string);
int m = strlen(pattern);
int s, p, *match;
if (m > n) return NotFound;
match = (int *) malloc(sizeof(int) * m);
// 查询match最长匹配字符串位置值 例如:图1-1
// pattern a b c a b
// index 0 1 2 3 4
// match -1 -1 -1 0 1
BuildMatch(pattern, match);
s = p = 0;
while (s < n && p < m) {
if (string[s] == pattern[p]) {
s++;
p++;
} else if (p > 0) {
// 将p置为 前p-1个元素 最大子串长度+1
// 如图1-2
p = match[p - 1] + 1;
} else
s++;
}
return (p == m) ? (s - m) : NotFound;
}
void BuildMatch(char *pattern, int *match) {
int i, j;
int m = strlen(pattern);
match[0] = -1;// -1 表示子串长度不存在,无任何相同的元素
for (int j = 1; j < m; ++j) {
// i表示前j-1个元素最大相同子串长度 数组索引位置 index-length 0-1
i = match[j - 1];
while ((i >= 0) && (pattern[i + 1] != pattern[j]))
// 第j个下标的字符和(match[j-1]+1)下标上的元素比较
// 如果不匹配,则根据下标为match[j-1]的相同串基础上进行条件比较
// 因为match[j-1]已经存在,那么绿紫色整块和后面绿紫块肯定一样
// 又第一个小绿块为match[match[j-1]],绿块和紫块相同
// 所以第一个绿块和最后一个紫块相同,只需比较问号位置的值即可
// char[match[match[j-1]]+1] 和 char[j] 的值是否相等
// 如图 1-3
i = match[i];
if (pattern[i + 1] == pattern[j])
// 如图 1-4
match[j] = i + 1;
// 如果都匹配不上就直接设置为-1
else match[j] = -1;
}
}
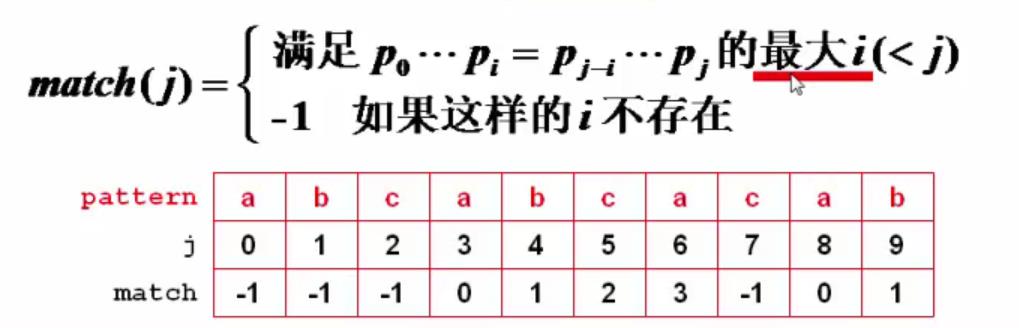
图1-1
match[j]的值实际上是前j个(包括j)元素的最大子串长度 对应到数组中的位置 比如图中 j = 6; 最大子串(abca)的长度为4,在数组中的索引为3

图1-2
当比较到后面不相等时,模式串相当于要后移到从上往下的第三个横条的情形,也就是把第二个横条情况p = match[p-1]+1

图1-3
- 第j个下标的字符和
(match[j-1]+1)下标上的元素比较 - 如果不匹配,则根据下标为
match[j-1]的相同串基础上进行条件比较 - 因为
match[j-1]已经存在,那么绿紫色整块和后面绿紫块肯定一样 - 又第一个小绿块为
match[match[j-1]],绿块和紫块相同 - 所以第一个绿块和最后一个紫块相同,只需比较问号位置的值即可
char[match[match[j-1]]+1]和char[j]的值是否相等
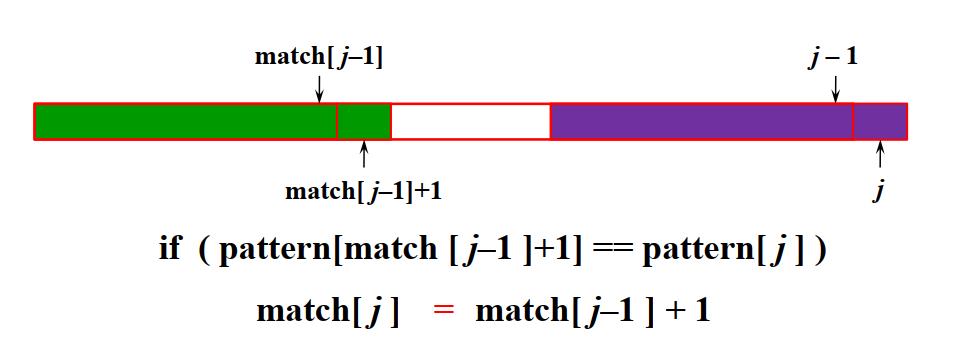
图1-4
以上是关于KMP(The Knuth-Morris-Pratt Algorithm)的主要内容,如果未能解决你的问题,请参考以下文章