决策树

Posted 2020-08-28 simple_wxl

 

六、分类树 VS 回归树

         提到决策树算法，很多想到的就是上面提到的ID3、C4.5、CART分类决策树。其实决策树分为分类树和回归树，前者用于分类，如晴天/阴天/雨天、用户性别、邮件是否是垃圾邮件，后者用于预测实数值，如明天的温度、用户的年龄等。

         作为对比，先说分类树，我们知道ID3、C4.5分类树在每次分枝时，是穷举每一个特征属性的每一个阈值，找到使得按照feature<=阈值，和feature>阈值分成的两个分枝的熵最大的feature和阈值。按照该标准分枝得到两个新节点，用同样方法继续分枝直到所有人都被分入性别唯一的叶子节点，或达到预设的终止条件，若最终叶子节点中的性别不唯一，则以多数人的性别作为该叶子节点的性别。

         回归树总体流程也是类似，不过在每个节点（不一定是叶子节点）都会得一个预测值，以年龄为例，该预测值等于属于这个节点的所有人年龄的平均值。分枝时穷举每一个feature的每个阈值找最好的分割点，但衡量最好的标准不再是最大熵，而是最小化均方差--即（每个人的年龄-预测年龄）^2 的总和 / N，或者说是每个人的预测误差平方和 除以 N。这很好理解，被预测出错的人数越多，错的越离谱，均方差就越大，通过最小化均方差能够找到最靠谱的分枝依据。分枝直到每个叶子节点上人的年龄都唯一（这太难了）或者达到预设的终止条件（如叶子个数上限），若最终叶子节点上人的年龄不唯一，则以该节点上所有人的平均年龄做为该叶子节点的预测年龄。 

 

ID3采用的信息增益度量存在一个内在偏置,它优先选择有较多属性值的Feature,因为属性值多的Feature会有相对较大的信息增益?(信息增益反映的给定一个条件以后不确定性减少的程度,必然是分得越细的数据集确定性更高,也就是条件熵越小,信息增益越大).避免这个不足的一个度量就是不用信息增益来选择Feature,而是用信息增益比率(gain ratio),增益比率通过引入一个被称作分裂信息(Split information)的项来惩罚取值较多的Feature,分裂信息用来衡量Feature分裂数据的广度和均匀性:

另外ID3只能处理离散型数据,Does not handle numeric attributes and missing values.

 

 

 

 

 

其中，对数据不需要任何加工指的是对缺失值的处理

 

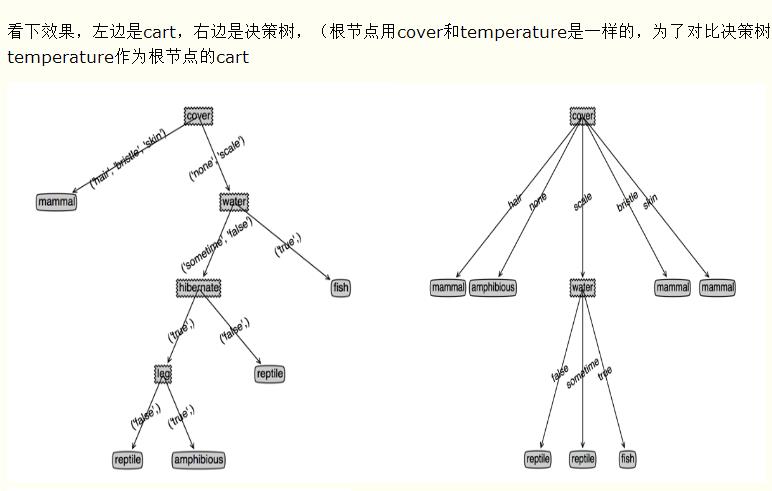
 gini基尼指数和C4.5的区别：

gini是二分类，C4.5是那个feature上有几类就分成几类