决策树算法

Posted 2021-10-09 秃头小苏

文章目录

• 决策树
• • 1. 决策树的整体理解
  • 2. 决策树的构造
  • • 2.1 决策树----熵
    • 2.2 构造决策树
  • 3. C4.5算法
  • 4. 决策树剪枝

决策树

1. 决策树的整体理解

​ 决策树，顾名思义，首先它是一棵树，其次，这棵树可以起到决策的作用（即可以对一些问题进行判断）。

​ 现通过下面的例子来理解决策树的作用。(注：决策树既可以做分类也可以做回归，此处主要讨论分类的决策树）图中共有五个人，现需要从中挑选出可能喜欢打篮球的人。那么我们就可以通过年龄和性别这两个指标去进行选择，第一步筛选出年龄小于15岁的两人，第二步通过性别就可以挑选出可能喜欢打篮球的人。[这里的年龄和性别被称为决策属性]

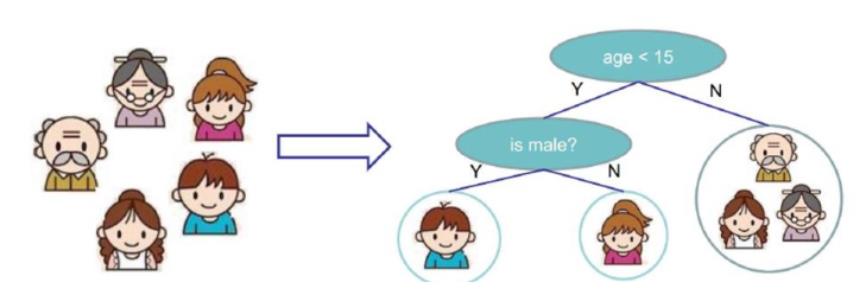
​ 通过上面的例子，我们可能会想决策树也太简单了，这不就是if语句进行判断吗？我早就会了。其实不然，上面的例子只是告诉我们决策树的使用，决策树更多的工作应该是在决策树的创建上。我们可以仔细想想这些问题，这个树为什么是这样的呢？为什么大于15岁就被分到不喜欢打篮球的一类呢？为什么女生就被分到不喜欢打篮球的一类呢？为什么要先对年龄属性进行判断呢，先判断性别属性可不可以呢？其实这些都是通过先前对决策树的构造来决定的。下面来介绍决策树的构造方法。

2. 决策树的构造

2.1 决策树----熵

​ 首先我们需要对熵有一个了解。高中化学中其实就有这样一个概念，他表示的是物体内部的混乱程度，或者说表示随机变量不确定性的度量。熵越大，表示物体内部越混乱，随机变量越不确定，即随机变量不确定性越大。

​ 若用H(X)表示事件X的不确定性，则

​ P(几率越大) --> H(X)值越小 【如夏天很热发生几率很大，那么它的不确定性(H(X)就很小)】

​ P(几率越小) --> H(X)值越大 【如冬天很热发生几率很小，那么它的不确定性(H(X)就很大)】

​ 下面为熵的公式：
$$熵=-{\sum }_{i=1}^n{P}_{i}In(P_i)$$
​ 我们可以从宏观上理解上面的熵公式：

上图的1>,2>反应了熵表示事件的不确定性，即一个事件发生的概率大，其不确定性H(x)越小，熵越小。

下面为Gini系数Gini§的公式，其表示的含义与熵类似。
$$Gini(p)=\sum _{k=1}^k{P}_k(1-P_k)=1-\sum _{k=1}^k{P}_k^2$$

举个例子进一步理解一下熵：假设现在有两个集合A = [1,2]，B = [1,1]

先分别计算两个集合中元素的熵。

A:熵 = - [1/2*In(1/2)+1/2*In(1/2)] = 0.693

B:熵 = - [1*In(1)+1*In(1)] = 0

通过计算可以发现熵A>熵B,即A比较混乱，从直观上我们也可以看出集合A比集合B混乱，这进一步验证了上面的结论。

2.2 构造决策树

​ 首先，我们需要知道构建决策树的基本思想，即随着树深度的增加，节点的熵迅速的降低。熵降低的速度越快，这样我们就有望得到一颗高度最矮的决策树。

​ 根据这个思想，我们举一个实例来说明。下表为根据outlook,temperature,humidity,

windy几个属性来决定是否打球的统计表。（表中共有14行数据，每个数据4个特征属性）

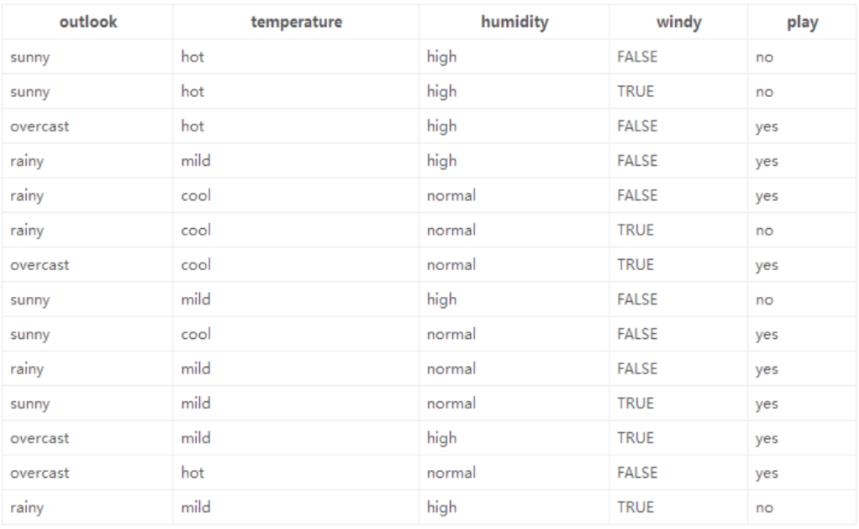
​ 在没有给定任何天气信息时，根据历史数据，我们得知新的一天中打球的概率为9/14,不打的概率为5/14,此时的熵为：
$$-\frac{9}{14}{\log }_2\frac{9}{14}-\frac{5}{14}{\log }_2\frac{5}{14}=0.940$$

​ 0.94就是我们初始时刻的熵值，前面说到构建决策树的基本思想就是使节点的熵迅速的下降。那么现在有4个属性(outlook, temperature, humidity,windy),每个属性都可以充当第一个节点，即根节点。这时我们就需要分别计算出4个属性充当根节点时的熵值，然后选择熵值下降最快的属性作为当前节点。

---

​ 首先，我们选择从outlook属性开始分析，从表中可以看出，outlook = sunny 共有5行数据（play标签栏有2个yes , 3个no）; outlook = overcast 共有4行数据（play标签栏全为yes ）;outlook = rainy共有5行数据（play标签栏有3个yes , 2个no）;其示意图如下：

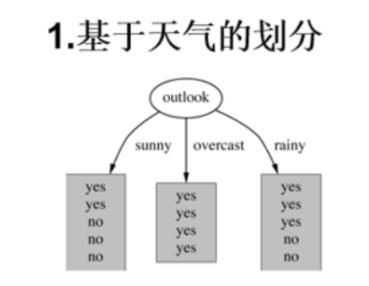
​ 下面计算其熵值（Entropy）：

​ 当outlook = sunny 时，Entropy = -2/5*log(2/5) - 3/5*log(3/5) = 0.971

​ 当outlook = overcast 时，Entropy = -1*log(1) - 0*log(0) = 0

​ 当outlook = rainy 时，Entropy = -3/5*log(3/5) - 2/5*log(2/5) = 0.971

​

​ 根据数据统计， outlook取值分别为sunny,overcast,rainy的概率分别为：5/14 , 4/14 , 5/14 。则其熵值为5/14*0.971 + 4/14*0 + 5/14*0.971 = 0.693。

​ 我们知道我们需要的节点是要使熵迅速下降的，那么我们不妨把熵下降的幅度定义为一个新的参数：信息增益gain。这样我们就可以通过比较信息增益的大小来判断选择什么节点作为当前节点。那么当选择outlook属性时的信息增益就是初始熵 - 变化熵：gain(outlook) = 0.940 - 0.693 = 0.247。

​ 同理我们可以得到其它属性的信息增益：

​ gain(temperature) = 0.029 ; gain(humidity) = 0.152 ; gain(windy) = 0.048

​ 我们发现属性outlook的信息增益最大，因此此时就选择outlook作为当前节点。确定好outlook作为根节点后，我们就可以对14条数据进行一些划分，然后在划分的数据中再采用相同的方法选择一个属性（除去outlook）作为这次划分的节点，以此往复，就可以得到一颗决策树。

3. C4.5算法

​ 上面通过信息增益来决定当前节点选择的算法称为ID3算法。但这种算法是存在缺陷的，我们举个例子 ，现在将前面的题增加一个ID属性，如图：

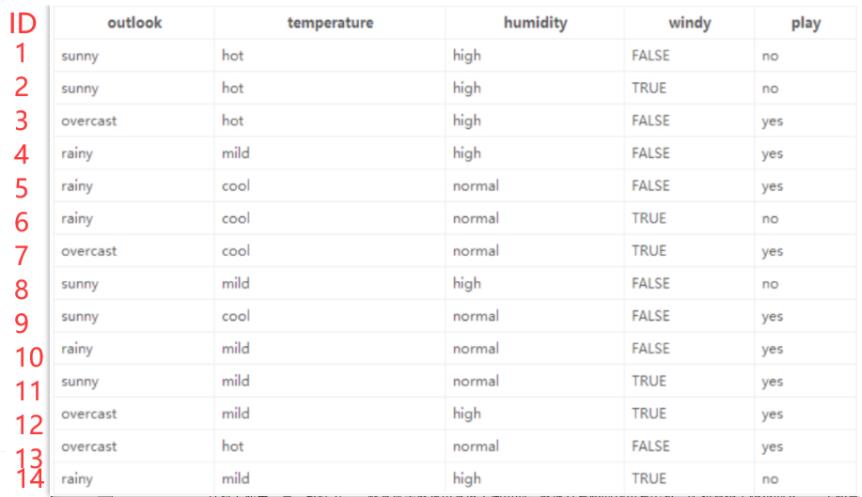
​ 现在计算ID属性的信息增益我们发现其信息增益为9.40，因为每个ID的play标签只有一个，都是确定的，其熵都为0。既然信息增益最大，是否可以说我们选择ID属性来进行划分是最优的呢？显然这是不合适的，因为ID属性和play标签是完全没有任何关系的。因此使用信息增益的ID3算法是有一定缺陷的。这里我们选择改进的C4.5算法，其是通过信息增益率GainRatio来实现的。信息增益率公式如下：
$$\mathrm{G}ainRatio(S,A)=\frac{gain(S,A)}{SplitInformation(S,A)}$$
​ 其中SplitInformation(S,A)为分裂信息度量，其定义如下：
$$SplitInformation(S,A)=-\sum _{i=1}^c\frac{|Si|}{|S|}{\log }_2\frac{|Si|}{|S|}$$
​ 其中 S1 到 Sc 是 c 个值的属性 A 分割 S 而形成的 c 个样例子集。 注意分裂信息实际上就是 S 关于属性 A 的各值的熵。

​ 其实，信息增益和信息增益率就和速度和加速的的区别类似。比如有两个跑步的人， 一个起点是 10m/s 的人、 其 10s 后为 20m/s； 另一个人起速是 1m/s、 其 1s 后为 2m/s。 如果紧紧算差值那么两个差距就很大了， 如果使用速度增加率(加速度， 即都是为 1m/s^2)来衡量， 2 个人就是一样的加速度。 因此， C4.5 克服了 ID3 用信息增益选择属性时偏向选择取值多的属性的不足。

​ 现用信息增益率来处理刚刚的ID属性，虽然ID属性的信息增益很大，但是要除以分裂信息度，SplitInformation(S,A)计算公式为：
$$SplitInformation(S,A)=-\sum _{i=1}^{14}\frac{|1|}{|14|}{\log }_2\frac{|1|}{|14|}$$
​ 上式中 SplitInformation(S,A)的值是非常大的，让其作为分母，会使信息增益率变得很小，那么就可以判断ID属性作为节点的效果不好。

4. 决策树剪枝

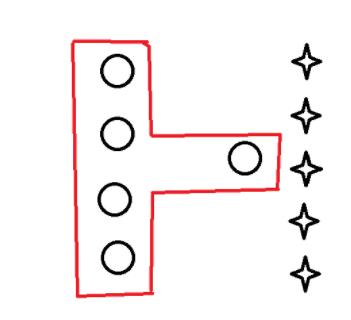
​ 我们先来看这样的例子，如图：有两种图形，我们训练数据最后达到的效果如下，即红框内的数据会被认为是圆，其它的数据会被认为是。这种训练结果好吗？只能说这个训练结果对已知的数据划分好，但是对未知的数据划分不好，这就是过拟合现象，那么我们怎么有效解决过拟合现象呢，这就需要对决策树进行剪枝。

​ 决策树剪枝主要有两种方法，预剪枝和后剪枝：

1. 预剪枝：在构建决策树的过程中，提前停止
2. 后剪枝：决策树构建好后，通过一定的衡量标准，对决策树进行裁剪

​ 决策树剪枝主要有两种方法，预剪枝和后剪枝：

1. 预剪枝：在构建决策树的过程中，提前停止
2. 后剪枝：决策树构建好后，通过一定的衡量标准，对决策树进行裁剪