决策树算法 CART和C4.5决策树有啥区别?各用于啥领域?
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了决策树算法 CART和C4.5决策树有啥区别?各用于啥领域?相关的知识,希望对你有一定的参考价值。
1、C4.5算法是在ID3算法的基础上采用信息增益率的方法选择测试属性。CART算法采用一种二分递归分割的技术,与基于信息熵的算法不同,CART算法对每次样本集的划分计算GINI系数,GINI系数,GINI系数越小则划分越合理。2、决策树算法是一种逼近离散函数值的方法。它是一种典型的分类方法,首先对数据进行处理,利用归纳算法生成可读的规则和决策树,然后使用决策对新数据进行分析。本质上决策树是通过一系列规则对数据进行分类的过程。
3、决策树算法构造决策树来发现数据中蕴涵的分类规则.如何构造精度高、规模小的决策树是决策树算法的核心内容。决策树构造可以分两步进行。第一步,决策树的生成:由训练样本集生成决策树的过程。一般情况下,训练样本数据集是根据实际需要有历史的、有一定综合程度的,用于数据分析处理的数据集。第二步,决策树的剪技:决策树的剪枝是对上一阶段生成的决策树进行检验、校正和修下的过程,主要是用新的样本数据集(称为测试数据集)中的数据校验决策树生成过程中产生的初步规则,将那些影响预衡准确性的分枝剪除。 参考技术A C4.5算法是在ID3算法的基础上采用信息增益率的方法选择测试属性。 ID3算法和C4.5算法虽然在对训练样本集的学习中可以尽可能多地挖掘信息,但其生成的决策树分支较大,规模较大。为了简化决策树的规模,提高生成决策树的效率,又出现了根据GINI系数来选择测试属性的决策树算法CART。
CART算法采用一种二分递归分割的技术,与基于信息熵的算法不同,CART算法对每次样本集的划分计算GINI系数,GINI系数,GINI系数越小则划分越合理。CART算法总是将当前样本集分割为两个子样本集,使得生成的决策树的每个非叶结点都只有两个分枝。因此CART算法生成的决策树是结构简洁的二叉树。
决策树
CART
简介
Classification And Regression Tree, 分类回归树,简称CART。通过前面文章的介绍知道了决策树的几种生成方法比如ID3, C4.5等。CART是决策树有一种常见生成方法,既可以用于分类,也可以用于回归。CART假设决策树是二叉树,即,特征取值为“是”或者“否”,且约定左分支为取值“是”,右分支为取值“否”。通过递归二分每个特征,将输入空间划分为有限个区块,每个区块对应某一个输出值。
那么如何划分呢?
CART生成
对回归树采用平方误差最小化原则,对分类树采用基尼指数(前面文章有介绍)最小化原则,进行特征选择生成二叉树。
回归树
回归树对应输入空间(特征空间)的一个划分,以及划分的区域上的输出值。假设将输入空间划分为M个区域(Region)R1, R2, ... , RM,每个区域上的输出值为cm,m=1,2, ... , M,于是回归树的模型,即函数为
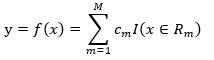 (1)
(1)
其中 I 函数在输入值x属于区域Rm时为1,否则为0。
注意回归中输出也是连续值(虽然这里得到还是离散值,因为实际中样本数量总是有限的,不过可以看作是阶跃函数),所以可以采用平方误差,在输入空间的划分确定后,对于某一个区域Rm,平方误差为输出真实值与模型值差的平方和(当然可以用开平方和,这里为了计算方便),
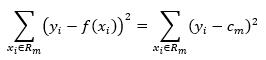 (2)
(2)
将平方误差最小化,则可以求得每个区域上的输出cm最优解,所以求(2)的极值,假设Rm上有n个样本点(虽然是回归是考虑的特征变量是连续型,但实际得到的样本都是离散的有限值),
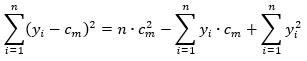 (3)
(3)
将(3)式求导,并令其等于0,
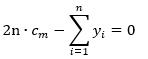
可以知道最优解为
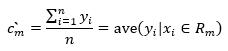 (4)
(4)
如此,就能求得每个区域Rm上的输出值。
以上是假设输入空间的划分已经确定之后所作的推导,那么问题来了,如何划分输入空间?这里采用启发式方法。
先任意选一输入特征,比如选择选择xj(注意,这里与前面保持相同的约定,上标表示维度,即输入的第j个特征),以及这个特征的一个取值s,作为切分变量和切分点,于是得到两个区域R1,R2

然后寻找最优切分变量j 和最优切分点s,具体地,就是为了让平方误差最小,求解
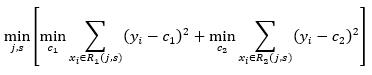 (5)
(5)
上式的含义是寻找j, s, c1, c2使得 R1, R2两个区域的平方误差最小,其中c1, c2分别是 R1, R2的输出值,根据(4)式,我们已经知道c1, c2的最优解为
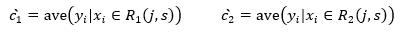
也就是说c1, c2是由 j, s 确定,所以问题最终变为寻找最优 j, s
由于特征维度有限,且样本点也有限,所以 j, s 的可能值个数也是有限的,所以一种简单的方法是,遍历所有可能的j, s 组合,寻找 (5)值,得到最优 j, s,于是将输入空间划分为 R1, R2,然后,再分别对这两个区域重复相同的过程,各自再划分为两个区域,直到满足停止条件(比如区域中只剩一个数据样本,或者区域中所有样本输出值相等,或者样本输出值的波动在一个很小的阈值之内),这样就生成了一棵回归树,这样的回归树通常称为最小二乘回归树(least squares regression tree)。
算法
输入:训练数据集D
输出:回归树f(x)
- 对某一区域R,选择最优切分变量j 和切分点 s。遍历变量 j,对某一切分变量j,扫描切分点s,对某一个切分点s,得到两个子区域R1, R2,然后计算最优输出值c1, c2,计算平方误差,如此下去,寻找 (5) 式的值,得到用对应的 j, s 值划分的区域R1, R2
- 递归地,分别对子区域R1, R2 进行步骤1,直到满足停止条件。
- 将输入空间划分为M个区域,R1, R2, ... , RM,(由于每一次都是二分切分,所以假设输入有J 维特征,则最终最多得到 2^J 个区域,因为考虑到停止条件,实际可能没这么多,M<=2^J,当然这个不重要),生成决策树由式(1)表示。
分类树
分类树使用基尼指数选择最优特征,同时确定该特征对应的切分点。
前面讲决策树的时候介绍过基尼指数了,这里再啰嗦一下,省得翻到前面的文章中查看。对于一个分类问题,假设共有K个分类值,输入系统中属于k分类的概率为pk,则系统的基尼指数为
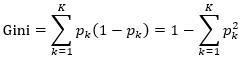 (6)
(6)
其含义是系统中本该是某一分类但实际又分类错误的可能性。基尼指数表征系统的不确定性,基尼指数越大,系统越不确定。比如抛硬币,正面向上概率为p,则反面向上概率为1-p,基尼指数为
Gini(0-1)=2*p*(1-p) (7)
当p=0.5时,基尼指数最大,此时正面和反面向上概率均为0.5,不确定性达到最大,不知道抛硬币是正面还是反面向上,而当p=0.9时,基尼指数减少,系统不确定性也减小,抛硬币倾向于认为正面向上,极端地,p=1,基尼指数达到最小(为0),此时系统不确定性也最小,因为每次抛硬币,毫无疑问,正面向上。
对于样本集D而言,基尼指数为
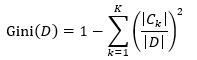 (8)
(8)
其中,|D|表示样本集D的数量,Ck表示分类值为ck的样本子集,|Ck|表示Ck的数量。
条件基尼指数
如果样本集合D根据特征A取值是否为a而被二分得到两个子集,
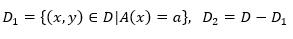
则给定特征A的条件下,集合D经过A=a分割后的条件基尼指数为
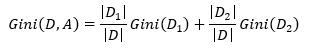 (9)
(9)
算法
输入:训练数据集D
输出:CART分类树
- 创建一个根结点,其切分属性和切分点以及子节点尚未确定,将训练数据集和根节点传给步骤2,此时可用特征为全部特征attrs。
- 对数据集D和对应节点node,分别计算每个可用特征对D的条件基尼指数。假设某一特征A,其可能的每个取值假设为a,根据数据集中样本点在特征A上取值是否为a,将数据集D划分为D1和D2两个子集,根据(8)和(9),计算条件基尼指数。选择条件基尼指数最小的A和对应的取值a,作为本次最优切分特征和切分点,将D切分为D1和D2两个子集。设置node节点切分属性为A,切分点为a,然后创建两个子节点(如果D1和D2不为空集),这两个子节点记为child1和child2,可用特征集合中去掉特征A。
- 递归地,对(D1,child1,attrs),(D2,child2,attrs),如果满足停止条件(比如子集中样本点个数为1,或者样本点所有分类值都相同或样本集使用(8)计算的基尼指数小于阈值,或者递归深度足够深,或者子集合中样本数量小于阈值,此时分类值选择占比最大的那个分类值,反正无论如何,满足停止条件时我们确保可用分类值只有一个,假设分类值为ck),则直接设置节点为叶节点,叶节点没有切分属性和切分点,故不需要设置,只需设置叶节点对应的分类值ck;如果不满足停止条件,则分别执行步骤2。
- 生成CART分类树
CART剪枝
与使用ID3或者C4.5策略生成的决策树一样,CART决策树也需要剪枝,使决策树变小(简单),从而避免过拟合,提高对未知数据的预测。这里剪枝过程是自下而上进行,从生成的决策树T0底端开始剪枝,直到T0的根节点变成一个单节点,形成一个子树序列{T0, T1,... , Tn}(具体如何剪枝请继续阅读下文)。通过交叉验证法在独立的验证数据集上对剪枝后的树进行测试,从中选择最优子树。显然,这是对任意子树整体来考虑损失函数,最选择损失函数最小的那个子树作为最优子树。(这里的子树指的是对决策树T0做某种剪枝后形成的新的决策树)
计算子树的损失函数
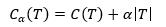 (10)
(10)
其中, T为子树序列中的任一子树。C(T)为子树对数据集的预测误差(如回归问题采用平方误差,分类问题采用基尼指数),|T|为子树的叶节点个数,α>=0为参数,Cα(T)为子树T的整体损失,包含预测误差和模型复杂度两部分。参数α权衡数据集的拟合程度和模型复杂度。
假设固定α,则一定存在损失函数最小的子树,将其表示为Tα,容易验证这样的最优子树是唯一的(可以通过对上面那个子树序列进行验证)。因为剪枝前C(T)比剪枝后C(T\')小(这一点我们前面就已经有过说明,简单来说就是,剪枝前更多的子节点可以有更多的分类来表示不同分类值的数据点,而剪枝后只能用一个分类表示不同分类值的数据点),而剪枝前模型复杂度|T|比剪枝后模型复杂度|T\'|大,也就是说C(T)与|T|变化趋势相反,所以固定α后,我们可以找到C(T)与α|T|的一个平衡,在某个子树上使得(10)式最小,这个子树就是最有子树。当α增大时,打破C(T)与α|T|的平衡,使得偏重α|T|,此时需要通过剪枝,降低α|T|从而重新找到平衡(虽然C(T)会增大,但是没关系,总会找到一个新的平衡),所以α增大时,最优子树Tα变小;反过来,α减小时,最优子树Tα变大。极端地,当α=0时,T0就是最优的(相当于此时没有考虑模型复杂度,生成的决策树是最优的,不需要剪枝,当然,这很理想);当α->无穷大时,根节点组成的单节点树是最优的(此时模型复杂度必须降到最低,当然,这是懒癌重症者嫌麻烦搞的最简单的树)。
所以我们得到这个结论:
α增大时,最优子树Tα变小;α减小时,最优子树Tα变大。
Breiman等人证明:可以用递归的方法对树进行剪枝。将α从小增大,0=α0<α1<...<αn<+∞,产生一些列的区间[αi,αi+1), i = 0,1, ... , n。剪枝得到的子树序列,序列中每个子树对应着区间α∈[αi,αi+1) 时的最优子树,即,α在不同区间中取值时的最优子树序列就是剪枝得到的子树序列,且序列中的子树是嵌套的(即T1是T0的子树,T2是T1的子树...这句话可以通过阅读下文对剪枝过程的阐述来理解)。
具体地,从整体树T0开始剪枝,对T0的任意内部节点t,考虑是否对节点t进行剪枝,
以t为单节点树的损失函数为
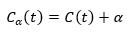
以t为根结点的子树Tt的损失函数为
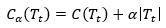
根据上面的讨论,当α足够小时,
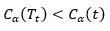
当α增大时,在某一αt处找到平衡,有
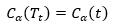
此后α继续增大,则有
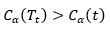
当α=αt时,Tt与t有相同的损失函数,而t的节点少,所以对Tt进行剪枝(α>αt时,同样是对Tt进行剪枝,下文可以看到我们其实要求的是最小的g(t),也就是最小的α,所以这里我们只关心α=αt的情况,αt也可以看成是一个阈值,我们关心这个阈值),
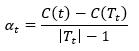
对T0中每一内部节点t,计算
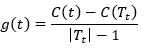 (11)
(11)
在T0中减去g(t)最小的Tt,得到的子树作为T1,同时将此时的g(t)记为α1,则T1就是区间[α1,α2)上的最优子树。
所以我们可以归纳一下,T0就是对应区间[α0,α1)上的最优子树,其中α0是已知的,为α0=0,增加α,当α达到min{g(t)}时,此时需要剪枝,根据上面的分析,此时的最优子树为次大的(仅比T0小),记为T1,所以T1就是区间[α1,α2)上的最优子树。然后对T1的所有内部节点,计算最小的g(t),此为α2,从T1中减去α2对应的内部节点,得到T2,所以T2就是区间[α2,α3)上的最优子树,如此剪枝下去,直到根节点(且没有内部节点可以剪枝,此时根节点必然有两个子节点,因为CART是二叉树),得到子树序列。
算法
输入:CART算法生成的决策树T0
输出:最优决策树Tα
- 令k=0,T=T0
- 令α=+∞
- 自下而上对树T的内部节点t分别计算C(Tt),|Tt|以及
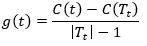 ,
,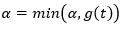
-
对各内部节点t,如果有g(t)=α,则进行剪枝,并对新的叶节点t以多数表决决定其类,得到树T
-
k=k+1,αk=α,Tk = T
- 如果Tk不是由根结点及两个叶节点组成的树,则跳至步骤2,否则对生成的子树序列{Tk|k=0,1, ... , n},使用交叉验证法计算各子树的平方误差或基尼指数,最小的值就是最优子树Tα
ref
- 统计学习方法,李航
示例代码
本示例代码仅考虑回归问题。代码正确未经验证,仅作帮助理解(上文)用。
CART节点类
public class CARTNode { ///// <summary> ///// 分裂属性的值类型:离散or连续? ///// </summary> //public ValType valType; /// <summary> /// 分裂属性的索引 /// </summary> public int j = -1; /// <summary> /// 分裂点值 /// </summary> public double splitVal; /// <summary> /// 父节点,剪枝阶段用到 /// </summary> public CARTNode parent; /// <summary> /// 输出值,叶节点才有 /// </summary> public double output = double.MinValue; public CARTNode() { } public void Update(CARTNode node) { this.j = node.j; this.splitVal = node.splitVal; this.output = node.output; this.region = node.region; } public List<CARTPoint> region; //------------- // 一个节点要么为叶节点,要么为非叶节点,根据这里的分裂逻辑,非叶节点必定是有两个子节点 //--------------- /// <summary> /// 左子节点,对应切点点值的左侧 /// </summary> public CARTNode left; /// <summary> /// 右子节点,对应切分点值的右侧 /// </summary> public CARTNode right; }
辅助类,提供上文的一些公式计算等。
public class CARTUtil { /// <summary> /// 获取以指定节点为根结点的子树中的所有叶节点 /// </summary> /// <param name="node"></param> /// <returns></returns> public static List<CARTNode> GetLeaves(CARTNode node) { var list = new List<CARTNode>(); var queue = new Queue<CARTNode>(); queue.Enqueue(node); while(queue.Count > 0) { var n = queue.Dequeue(); if (n.left == null) list.Add(n); else { queue.Enqueue(n.left); queue.Enqueue(n.right); } } return list; } /// <summary> /// 获取方差,作为回归问题中的预测误差 /// </summary> /// <param name="points"></param> /// <returns></returns> public static double GetVar(CARTNode node) { double ave = 0; if (node.left != null) ave = node.region.Sum(p => p.vals.LastOrDefault()) / node.region.Count; else ave = node.output; return node.region.Sum(p => Math.Pow(p.vals.LastOrDefault() - ave, 2)); } /// <summary> /// 给定切分变量j,计算最小平方误差 /// 切分点根据样本中相邻切分属性值的中间值逐一选择 /// </summary> /// <param name="j">切分属性的索引</param> /// <param name="points">区域中的数据点集合</param> /// <returns></returns> public static TempResult SquareError(int j, List<CARTPoint> points) { var t_idx = points[0].vals.Length - 1; CARTSort(points, j); // 根据j属性值升序排序 var list = GetSplitVals(points, j); double minError = double.MaxValue; double split_val = 0; List<CARTPoint> region_1 = null; List<CARTPoint> region_2 = null; for(int i = 0; i < list.Count; i++) { var tuple = list[i]; var region1 = points.Take(tuple.Item1 + 1).ToList(); var region2 = points.Skip(tuple.Item1 + 1).ToList(); var c1 = EstimateY(region1); var c2 = EstimateY(region2); double squreError = 0; foreach(var p in region1) { squreError += (p.vals[t_idx] - c1) * (p.vals[t_idx] - c1); } foreach (var p in region2) { squreError += (p.vals[t_idx] - c2) * (p.vals[t_idx] - c2); } if (minError > squreError) { minError = squreError; split_val = tuple.Item2; region_1 = region1; region_2 = region2; } } return new TempResult() { splitVal = split_val, region1 = region_1, region2 = region_2 }; } private static double EstimateY(List<CARTPoint> points) { var t_idx = points[0].vals.Length - 1; return points.Sum(p => p.vals[t_idx]) / points.Count; } /// <summary> /// 根据 j属性,获取排序后的样本的切分位置,比如切分位置为i,则切分为{e|idx <e; i -1, idx >= 0}, {e|idx > i, idx < Count} /// 增加Item2,表示切分点值 /// </summary> /// <param name="points"></param> /// <param name="j"></param> /// <returns></returns> private static List<Tuple<int, double>> GetSplitVals(List<CARTPoint> points, int j) { var list = new List<Tuple<int, double>>(); var t_idx = points[0].vals.Length - 1; // 输出属性的索引 //double prev = double.MinValue; // 上一个样本点的 j 属性值 for(int i = 0; i < points.Count; i++) { var start = points[i]; //prev = start.vals[j]; for(int k = i + 1; k < points.Count;k++) { var cursor = points[k]; // 如果输出属性相等则这两个相邻样本点之间不设置切分点,从而减少计算量 if (cursor.vals[t_idx] == start.vals[t_idx]) continue; // 如果输出属性不相等,则 var idx = k - 1; var s = (cursor.vals[j] + points[k - 1].vals[j]) / 2; list.Add(new Tuple<int, double>(idx, s)); } } return list; } /// <summary> /// 根据j属性值升序排序,排序是为了更好的确定切分点,以及在可能的情况下减少切分点数量,从而减少计算量 /// </summary> /// <param name="points"></param> /// <param name="j"></param> private static void CARTSort(List<CARTPoint> points, int j) { var t_idx = points[0].vals.Length - 1; // 输出属性的索引 // 插入排序,故意避免递归 for(int i = 1; i < points.Count; i++) { if(points[i-1].vals[j] > points[i].vals[j]) { var temp = points[i]; int k = i; while(k >0 && points[k -1].vals[j] > temp.vals[j]) { points[k] = points[k - 1]; k--; } while(k > 0 && points[k-1].vals[j]== temp.vals[j] && points[k - 1].vals[t_idx] > temp.vals[t_idx]) // 需要进行二级排序 { points[k] = points[k - 1]; k--; } points[k] = temp; } // 如果 j 属性值相等,则进行二级排序,按输出属性值升序排序 else if(points[i-1].vals[j] == points[i].vals[j]) { if(points[i-1].vals[t_idx] > points[i].vals[t_idx]) { var temp = points[i]; int k = i; while(k > 0 && points[k-1].vals[j] == temp.vals[j] && points[k-1].vals[t_idx] > temp.vals[t_idx]) { points[k] = points[k - 1]; k--; } points[k] = temp; } } } } }
临时类,用于保存中间数据
public class TempResult { /// <summary> /// 损失函数值 /// </summary> public double lossVal; /// <summary> /// 分裂点值 /// </summary> public double splitVal; /// <summary> /// 子区域1 /// </summary> public List<CARTPoint> region1; /// <summary> /// 子区域2 /// </summary> public List<CARTPoint> region2; }
CART样本数据类
public class CARTData { /// <summary> /// 属性数量,包括输出 /// </summary> public int J; /// <summary> /// 训练数据集 /// </summary> public List<CARTPoint> trainSet = new List<CARTPoint>(); /// <summary> /// 离散值到实数的映射 /// key: 属性索引, value: 离散值到实数的映射 /// </summary> public Dictionary<int, Dictionary<string, double>> disc2Real = new Dictionary<int, Dictionary<string, double>>(); /// <summary> /// key:属性索引,value: 实数到离散值的映射,以实数为索引得到的elem值为属性离散值 /// </summary> public Dictionary<int, string[]> real2Disc = new Dictionary<int, string[]>(); /// <summary> /// 属性名和对应的值类型 /// </summary> public List<string> attrNames = new List<string>(); /// <summary> /// 验证数据集 /// </summary> public List<CARTPoint> verifySet = new List<CARTPoint>(); public void Init(string path) { var lines = File.ReadAllLines(path); int flag = 0; // 1: train-data; 1: verify-data foreach(var line in lines) { if (string.IsNullOrWhiteSpace(line)) continue; if(line.StartsWith("@ATTRIBUTE")) { var segs = line.Split(new[] { \'\\t\', \' \' }, StringSplitOptions.RemoveEmptyEntries); attrNames.Add(segs[1]); if(segs[2] != "cont") { var vals = segs[3].Split(\'/\'); real2Disc.Add(J, vals); var dict = new Dictionary<string, double>(); for(int i = 0; i < vals.Length; i++) { dict.Add(vals[i], i); } disc2Real.Add(J, dict); } J++; } else if(line.StartsWith("@train-data")) { flag = 1; } else if(line.StartsWith("@verify-data")) { flag = 2; } else { var segs = line.Split(new[] { \' \', \'\\t\' }, StringSplitOptions.RemoveEmptyEntries); var point = new CARTPoint(segs.Length); for(int i = 0; i < segs.Length; i++) { double d; if(!double.TryParse(segs[i], out d)) { // 离散值,获取对应的映射实数 d = disc2Real[i][segs[i]]; } point.vals[i] = d; } if(flag == 1) { // 训练数据 trainSet.Add(point); } else { // 验证数据 verifySet.Add(point); } } } } }
其中样本数据点类为
/// <summary> /// 样本数据点 /// </summary> public class CARTPoint { /// <summary> /// 数据点各属性的值,最后一个属性表示输出 /// 如果是离散型属性,将离散型值映射为实数 /// </summary> public double[] vals; public CARTPoint(int d) { vals = new double[d]; } }
CART决策树类
class CARTTree { private CARTNode _root; public CARTNode Root { get { return _root; } } /// <summary> /// 根据样本数据创建CART决策树 /// </summary> /// <param name="data"></param> /// <returns></returns> public static CARTTree Create(CARTData data) { var tree = new CARTTree() { _root = new CARTNode() }; var attrIdxs = Enumerable.Range(0, data.J - 1).ToList(); // 输入属性索引列表 Create(tree._root, attrIdxs, data.trainSet); return Prune(tree, data); } /// <summary> /// 生成决策树 /// </summary> /// <param name="node"></param> /// <param name="attrIdxs"></param> /// <param name="points"></param> private static void Create(CARTNode node, List<int> attrIdxs, List<CARTPoint> points) { node.region = points; // 根据CART分裂策略,分裂后的区域内样本点数量至少为1,不可能为0 if (points.Count == 1) { // 如果为1,则不再分裂,直接设置为叶节点 node.output = points[0].vals.LastOrDefault(); } else { var ave = points.Sum(p => p.vals.LastOrDefault()) / points.Count; // 没有可用于分裂的属性,则设置叶节点 // 输出值的估计为区域中样本点输出值的均值 if (attrIdxs.Count == 0) { node.output = ave; } else { // 先计以上是关于决策树算法 CART和C4.5决策树有啥区别?各用于啥领域?的主要内容,如果未能解决你的问题,请参考以下文章