离散时间信号与系统：4

Posted 2020-08-25 御剑飞行

14.系统

系统就是变换（Transformations，在线性代数中表示运动的一种描述）.将一个离散时域信号x映射到一个离散时域信号y。例如：磁共振成像系统。

 与有限信号的和无限信号相对应的处理有限信号的系统和无限信号的系统。

其中，offset翻译成：补偿系统么？ Decimate 翻译成抽样系统么？

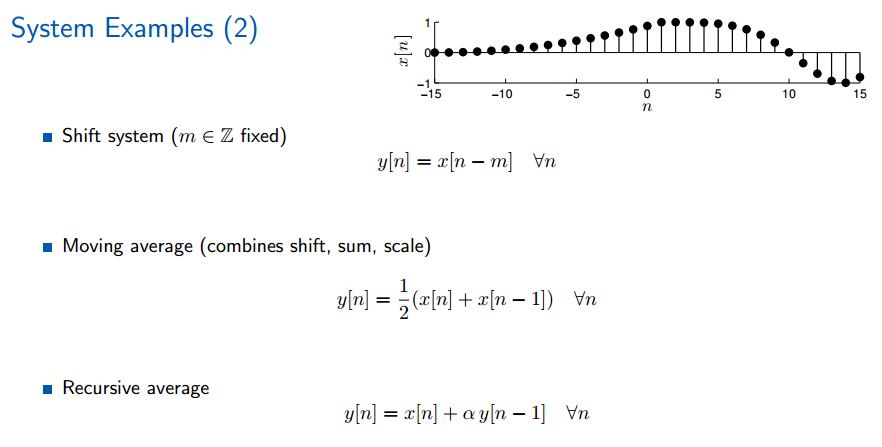
总结：

系统通过对信息的操作将一个信号变换为（transform）另一个信号。

将无限信号x变换为无限信号y。

将长度为N的信号x变换为长度为N的信号y。

15. 线性系统

两个性质： 缩放性和可加性。

注意：两个性质都是系统输出y随着系统输入x的变化。而对应信号中x[n]的整体变化，不是n的变化。（时不变是关于n的）

证明系统线性，需要证明系统对任意输入信号都保持两个性质。而证明非线性只需要一个返例。

矩阵相乘和线性系统的关系，写在前面：线性代数就是描述线性变化的学科，主要手段就是矩阵相乘。所以他们联系自然紧密。

矩阵相乘就是一个线性系统。所有的线性系统都可以表达为矩阵相乘。

这个结论非常imba，想想工科研究，都是对各种模型系统进行的，而这些系统基本上都是线性系统！！！  所以，都是矩阵相乘。

 

使用图像的形式对线性系统进行表达，还是蛮有趣的一件事。而图像的表达也是很多线性系统研究的方式之一。

线性系统可以看成矩阵H的列向量的线性组合，x是权值向量，y是输出。 

线性系统也可以看做是一系列的内积。每个y[n]都是H矩阵中的第n行与x的内积。

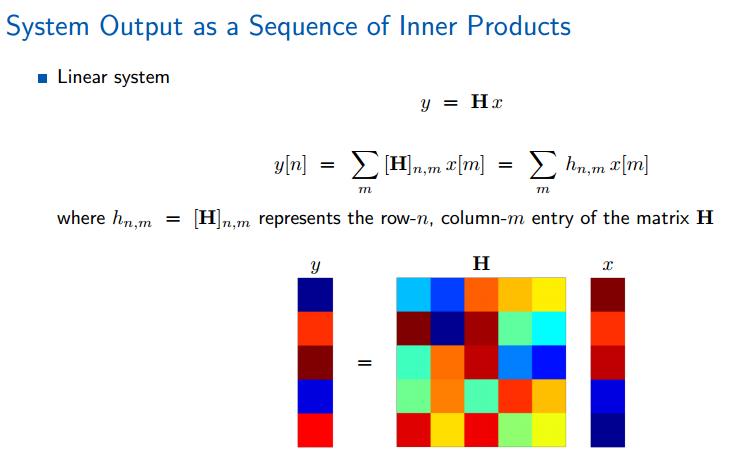
除了以上两种理解：

从线性代数的角度看，矩阵相乘就是向量的线性变换（从空间的一个点变换到另一个点），或者说该点不变，而是空间本身的变换。相关链接：矩阵的理解这篇文章。

 总结：

线性系统的性质。

线性系统h可以表达为一个矩阵（H），所以可以从两个角度理解：

系统输出y可以看做是矩阵H的加权平均，权值是x。

系统输出y也可以看成是H的行向量和x的内积的序列。

16.时不变系统(也叫移不变系统)

一个系统昨天输入x，今天输入x，明天输入x，任何时间输入x都只得到同样的输出y。输出只与x[n]的值有关，与时间n无关，为什么强调这个？ 因为信号是x[n]是时间的函数呀。所以时不变系统与n的变化无关！！！！ 

同样时间位移产生同样的时间位移的输出。同样时间位移产生同样的时间位移的输出。同样时间位移产生同样的时间位移的输出。

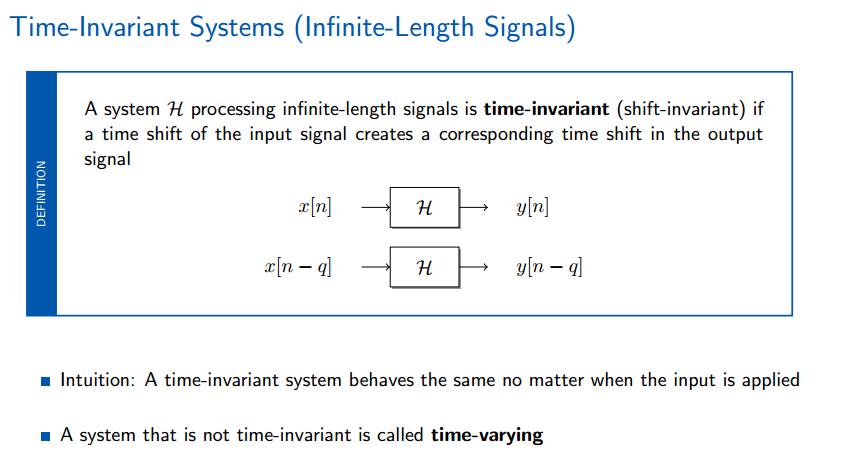
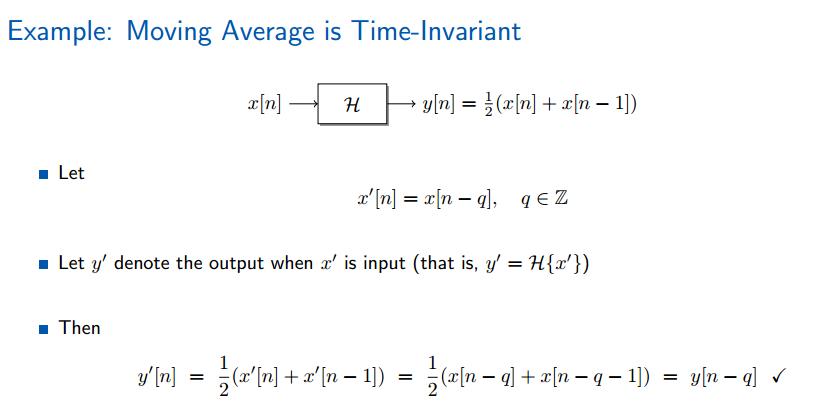
有限信号的时不变系统与无限信号的区别之处为：有限信号的移位通过模操作（圆环）来完成，还记得么？ （第一章中有）。所以在表达式上使用模操作。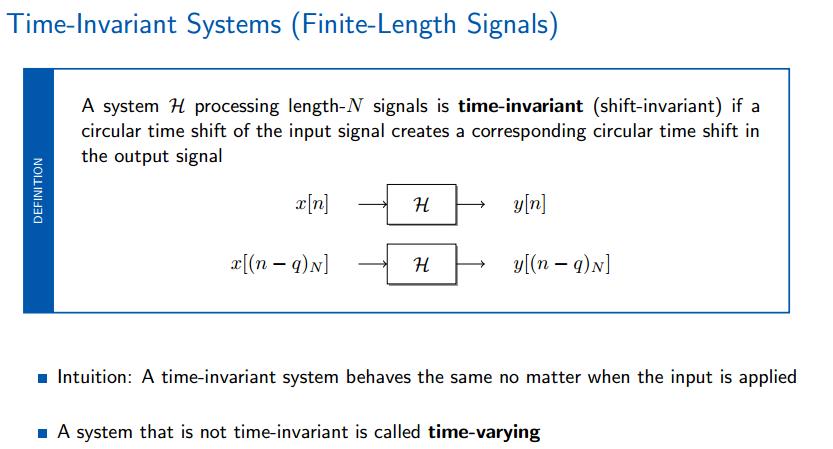

总结：

时不变系统的性质不变，不论什么时间进行输入。

无限信号：任何整数的时间位移，系统皆保持不变。

有限信号：任何环状时间位移，系统皆保持不变。

 

17.线性是不变系统

同时含有线性和时不变两个性质的系统。

 

 

有趣的地方出现了！！！有趣的地方出现了！！！有趣的地方出现了！！！

线性时不变系统的矩阵H是非常特殊的。输出y[n]是H的第n行，与x信号的内积，即每个h_n,m与x[m]相乘再累加。(因为系统的输出只与输入x有关系，而H不变，即h也不变)

当该系统是时不变系统时，则将n-q带入系统，相当于信号向右移动了q位，所以在计算时，x的表示为x[m-q]。

由h构成的矩阵H叫做托普利兹矩阵，托普利兹矩阵，托普利兹矩阵。该矩阵的特点是： 对角线方向上的元素全部相同。

而这个性质使得通过个一个向量就可以存储整个矩阵的信息.

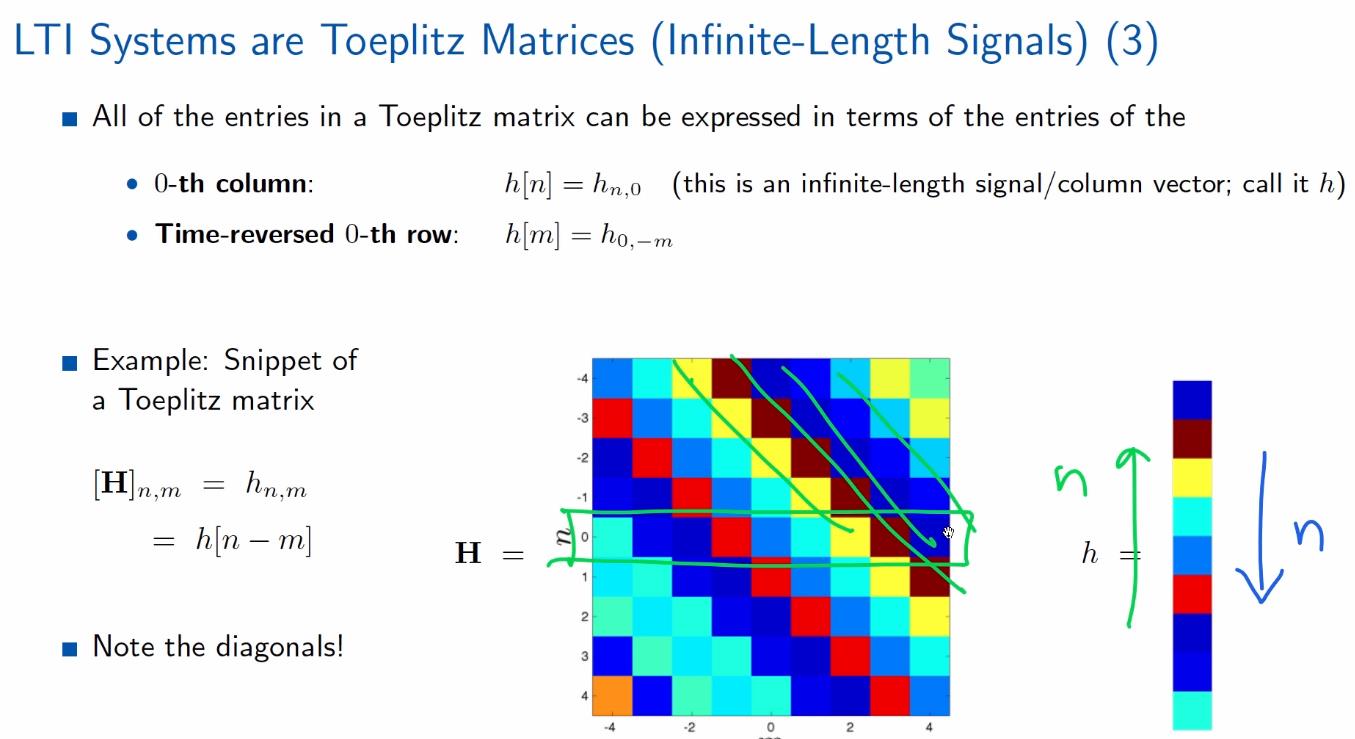
第0行和第0列(H中两个非常特殊向量): 第0列就含有全部信息（注意0的位置，在矩阵的中心），H矩阵的其他元素都是沿着对角线方向复制第0列;另外，第0行的时间反序=第0列.

根据上面性质，得到新的矩阵表示形式，每个元素的值h_n,m=h[n-m]

注意：[n-m]的值在对角线位置处永远相同，所以h[n-m]中无论n-m的结果是多少，在h上一定有个元素与之对应，所以该表达可以表示任何元素。

 

线行时不变系统的矩阵结构（有限长度信号）-Matrix Structure of LTI Systems (Finite-Length Signals)

长度为N的输入信号，经过线性系统，得到长度为N的输出信号。其矩阵表示为：第n个输出信号y[n]等于H矩阵的第n行，该行的每个对应第m个元素与输入信号x的第m个元素相乘，最后再相加。

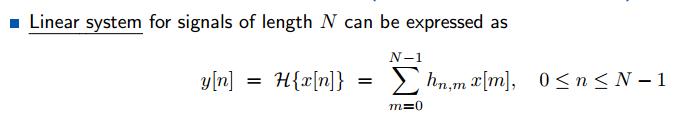
对系统加入时不变性质，即输入x[n-q]对应输出y[n-q]。所以系统H矩阵不变，而原来的m元素变为m-q（注意m和n的转换，因为H用n表示行，所以用m表示元素个数），通过模运算表示为：(m-q)_N

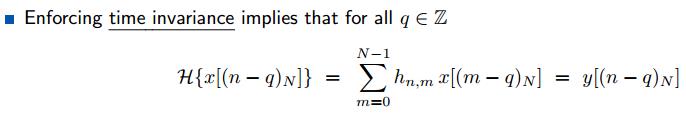
进一步将n\'=n-q合m\'=m-q进行代替，这一步就是将系统的表达换为x[n]和y[n]的形式，注意H坐标的变化。

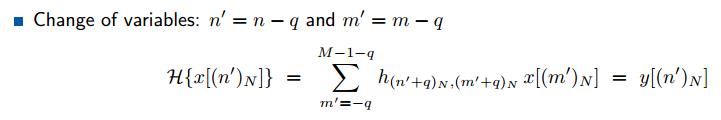
所以，我们得到了输入为x[n],对应输出为y[n]，所以说明H矩阵具有特殊形式如下：

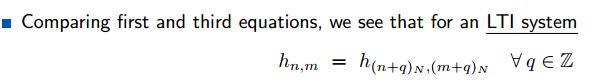
将矩阵全部表示出来，就是对角线方向的值完全相同：

同样,第0行和第0列是两个特殊的向量:

矩阵是个循环矩阵:

H可以通过第0列进行不断的循环位移得到,第2列就是第1列向下(正方向)一定1位.

H也可以通过第0行进行不断的循环位移得到,例如第2行就是第1行向右(正方向)移动1位.

注意：后面的矩阵只需用一个序号n就可以了，这个在卷积的计算中太有用了！！！这个在卷积的计算中太有用了！！这个在卷积的计算中太有用了！！

第0行的循环时序反转是如何运行的？

 

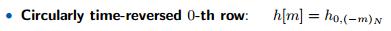
h0,0是不变的。而m=1时表示在长度为N的圆环中向反方向旋转1位，即得到最后一个元素（第N-1个），即棕色的像素。同理依次得到h[m]的所有元素（与第0列完全相同）。

所以，这个循环时序反转是根据环状模运算得到改向量中的所有分量，结果是h[o]元素就是取环中的0号元素，而从h[1]开始则从该环中的最后一个开始时间倒序取值。这点与无限信号十分不同，无限信号中直接将第0行的向量进行关于m=0点对称翻转即可。

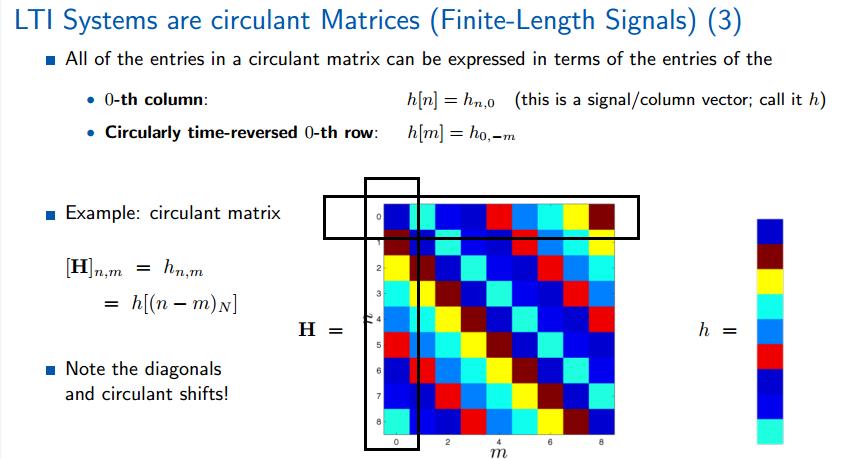
总结：

线性时不变系统=线性+时不变。是信号处理系统的基础。

无限信号系统=托普利兹矩阵（Toeplitz matrix H），该矩阵具有特殊形式：

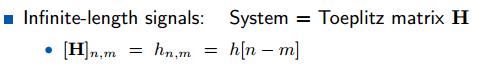
 与之对应，有限信号的系统为循环矩阵（circulant matrix ）

 

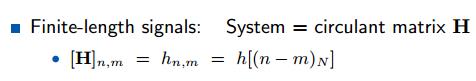
这两个矩阵不再使用下标表示矩阵，很重要。