求50以内的所有勾股数

Posted 2023-03-29

告诉我多少组也可以?

勾股数一般形式：a=m^-n^，b=2mn，c=m^+n^，m,n∈N,m>n

要求：a,b,c≤100且(a,b,c)=1---->(m,n)=1

n=1,m=2时:(3,4,5)；
n=1,m=4时:(15,8,17)；
n=1,m=6时:(35,12,37)；
n=1,m=8时:(63,16,65)；
n=2,m=3时:(5,12,13)；
n=2,m=5时:(21,20,29)；
n=2,m=7时:(45,28,53)；
n=2,m=9时:(77,36,85)；
n=3,m=4时:(7,24,25)；
n=3,m=8时:(55,48,73)；
n=4,m=5时:(9,40,41)；
n=4,m=7时:(33,56,65)；
n=4,m=9时:(65,72,97)；
n=5,m=6时:(11,60,61)；
n=5,m=8时:(39,80,89)；
n=6,m=7时:(13,84,85)。

∴100以内的勾股数共有以上16组。 参考技术A 勾股数可以由复整数的平方运算完整生成。
其原理如下：(a+bi)^2=a^2+2abi+(bi)^2=(a^2-b^2)+2abi,
|(a+bi)^2|=sqrt((a^2-b^2)^2+(2ab)^2)=a^2+b^2.
∴(a^2-b^2)^2+(2ab)^2=(a^2+b^2)^2

由此可以通过复整数的平方来遍历产生所有勾股数。
下面求100以下的所有勾股数。
a^2+b^2<100, ∴a<10, b<10。
由于对称性，不妨设a>b。

(2+i)^2=3+4i, (3,4,5);

(3+i)^2=8+6i, (8,6,10)与(3,4,5)存在倍数关系;
(3+2i)^2=5+12i, (5,12,13);

(4+i)^2=15+8i, (15,8,17);
(4+2i)^2=12+16i, (12,16,20)与(3,4,5)存在倍数关系;
(4+3i)^2=7+24i, (7,24,25);

(5+i)^2=24+10i, (24,10,26)与(5,12,13)存在倍数关系;
(5+2i)^2=21+20i, (21,20,29);
(5+3i)^2=16+30i, (16,30,34)与(15,8,17)存在倍数关系;
(5+4i)^2=9+40i, (9,40,41);

(6+i)^2=35+12i, (35,12,37);
(6+2i)^2=32+24i, (32,24,40)与(3,4,5)存在倍数关系;
(6+3i)^2=27+36i, (27,36,45)与(3,4,5)存在倍数关系;
(6+4i)^2=20+48i, (20,48,52)与(5,12,13)存在倍数关系;
(6+5i)^2=11+60i, (11,60,61);

(7+i)^2=48+14i, (48,14,50)与(7,24,25)存在倍数关系;
(7+2i)^2=45+28i, (45,28,53);
(7+3i)^2=40+42i, (40,42,58)与(21,20,29)存在倍数关系;
(7+4i)^2=33+56i, (33,56,65);
(7+5i)^2=24+70i, (24,70,74)与(35,12,37)存在倍数关系;
(7+6i)^2=13+84i, (13,84,85);

(8+i)^2=63+16i, (63,16,65);
(8+2i)^2=60+32i, (60,32,68)与(15,8,17)存在倍数关系;
(8+3i)^2=55+48i, (55,48,73);
(8+4i)^2=48+64i, (48,64,80)与(3,4,5)存在倍数关系;
(8+5i)^2=39+80i, (39,80,89);
(8+6i)^2=28+96i, (28,96,100)与(7,24,25)存在倍数关系, 最大值等于100;*
(8+7i)^2=15+112i, (15,112,113), 最大值超过100;*

(9+i)^2=80+18i, (80,18,82)与(9,40,41)存在倍数关系;
(9+2i)^2=77+36i, (77,36,85);
(9+3i)^2=72+54i, (72,54,90)与(3,4,5)存在倍数关系;
(9+4i)^2=65+72i, (65,72,97);
(9+5i)^2=56+90i, (56,90,106)与(45,28,53)存在倍数关系, 最大值超过100;*
(9+6i)^2=45+108i, (45,108,117)与(5,12,13)存在倍数关系, 最大值超过100;*
(9+7i)^2=32+126i, (32,126,130)与(63,16,65)存在倍数关系, 最大值超过100;*
(9+8i)^2=17+144i, (17,144,145), 最大值超过100;*

所以100以下的勾股数共有30组，其中独立的有16组。
50以下的勾股数共13组，其中独立的有7组。
独立的条件：a,b不能同时为奇数，不能同时为偶数，且a,b互素。 参考技术B 4 3 5 6 8 10 5 12 13……

勾股数

程序地址：http://www.cheemoedu.com/exercise/16

问题描述：

所谓勾股数，一般是指能够构成直角三角形3条边的3个正整数（a,b,c)。
即a2+b2=c2，a，b，cΣN
求1000以内的勾股数。

我的思路：使用for循环列出所有的数，连续判断是否满足a2+b2=c2关系，满足的就是勾股数，但是要注意，三个数中任意一个都不可以为0，且重复的如3,4,5和4,3,5要去除，只留下其中一个；

我的代码：

for i in range(1,1000):
    for j in range(i+1,1000):
        for k in range(1000):
            if i**2+j**2==k**2:
                print i,j,k

示例代码：

import math
for a in range(1, 1000):
    for b in range(a + 1, 1000):
        c = math.sqrt(a * a + b * b)
        if c > 1000:
            break
        if c.is_integer():
            print a, b, int(c)

代码分析：想来想去也就想到了这个写法，但是很明显，我的代码很臃肿，运行速度非常慢，效率也非常低，毕竟基数大，还用了三个for循环。

而示例代码明显比我的高效，它只循环了两次，使用math模块的sqrt函数求得a2+b2的平方根值(注意该值的类型为浮点型，不是整型),然后判断该值是否在1000以内，并且判断该值是否为有限的浮点型数，如果是就打印出a,b和整型化的c；

总结：

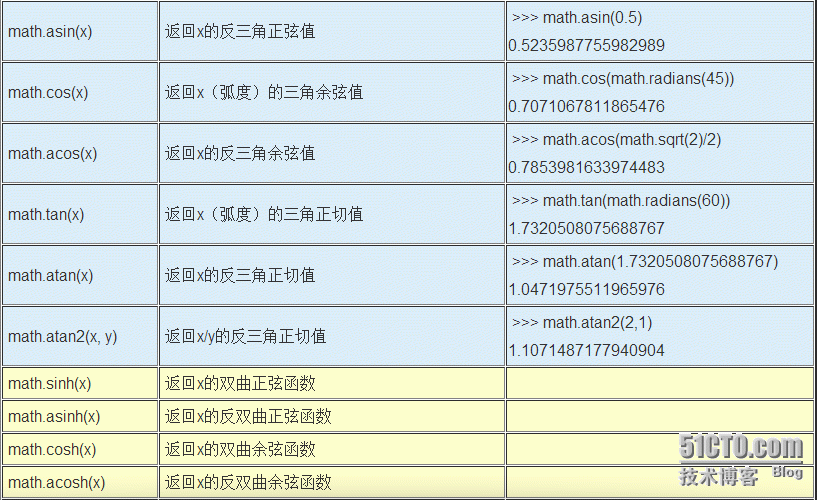
1. math模块的函数说明

2.关于is_integer的说明：

is_integer就是判断一个浮点数是否是有限的，如果是就返回True，否则返回False；

http://python-reference.readthedocs.io/en/latest/docs/float/is_integer.html