算法之美--2.3.1 Z字形编排问题

Posted 2020-08-22 小河沟大河沟

 2016-12-08   00:23:11

写在前面的话：万事贵在坚持，万事开头难，有很多的东西要学，要知道主次，讲究效率，大的方向对就行！坚持........

 

一、图像压缩编码中的Z字排序

JPEG（Joint Photographic ExpertsGroup）是一种常见的图像文件格式，也是目前静态图像中压缩比最高的一种图像文件格式，它综合运用了多种压缩技术而达到一种极高的压缩比例。JPEG是作为一个国际数字图像压缩标准，压缩技术十分先进，它用有损压缩方式去除冗余的图像和彩色数据，获取得极高的压缩率的同时能展现十分丰富生动的图像。目前，它已被广泛地应用与多媒体和网络程序中。通常，在JEPG编码过程中，有一个非常重要的步骤，即Z字形编排过程。Z字形编排过程大致是这样的：经过前期处理的图像被分为若干个 的小图像块，此时就从小图像块的左上角开始沿Z字形对图像元素进行遍历，并将遍历所得的结果重新写入等大小的图像块中，整个过程如图2-15所示。

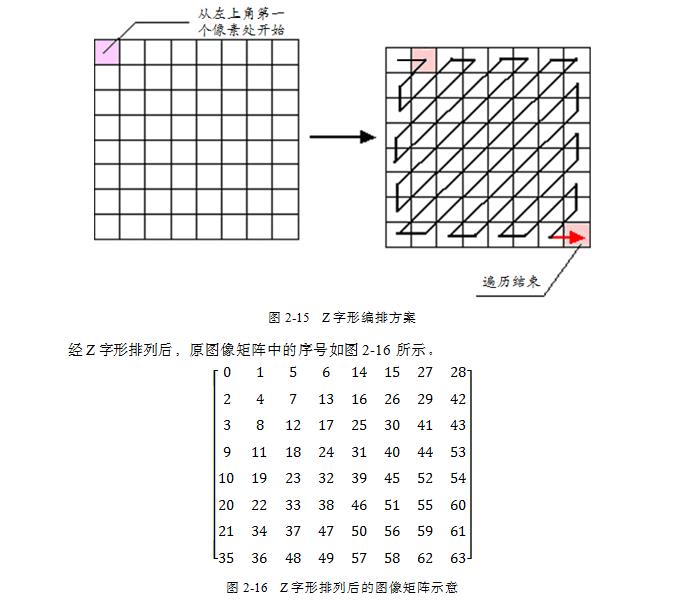
要实现这样一个Z字形排列可能读者咋一看会感觉无从下手。但是在分析了Z字形遍历原矩阵过程中的走向规律，其实可以设计一个非常简单的算法来实现这种编排。对于原始矩阵matrix中的任意元素matrix[i][j]的遍历走向规律可以分为如下三种情况

• 如果二维数组中的元素matrix[i][j]中纵坐标j是偶数，且i=0或者i=7，那么遍历路径在矩阵中的走向就是水平向右移动一格。

• 如果二维数组中的元素matrix[i][j]中纵坐标i是奇数，且j=0或者j=7，，那么遍历路径在矩阵中的走向就是垂直向下移动一格。

• 除上述规则以外的情况，如果二维数组中的元素matrix[i][j]的横纵坐标和i+j是偶数，则遍历路径在矩阵中的走向就是右上角移动一格；否则，若i+j是奇数，则遍历路径在矩阵中的走向就是左下角移动一格。

#include <iostream>
#include <iomanip>

using namespace std;

#define  SIZE 8
int main(int argc, char **argv[])
{
    int matrix[SIZE][SIZE] = {0};
    int a[SIZE][SIZE] = { 0 };
 
    int *p = nullptr;
    p = &matrix[0][0];
    //初始化矩阵
    for (int k = 0; k < SIZE*SIZE; k++)
    {
        *p++ = k;
    }
    //打印原始矩阵
    cout << "原始矩阵如下：" << endl;
    for (int k= 0;k < SIZE;k++)
    {
        for (int h = 0; h < SIZE;h++)
        {
            cout << setw(4) << *(*(matrix + k) + h);
        }
        cout << endl;
    }

    //Z字形编排
    int i = 0, j = 0;  //变量不能重复
    for (int x = 0; x < SIZE;x++)
    {
        for (int y = 0; y < SIZE;y++)
        {
            *(*(a + i) + j) = *(*(matrix + x) + y);

            if((i==SIZE-1||i==0)&&j%2==0)  //水平右移
            {
                j++;
                continue;
            }
            if ((j==0||j==SIZE-1)&&i%2==1) //垂直下移
            {
                i++;
                continue;
            }
            if ((i+j)%2==0)        //右上
            {
                i--; 
                j++;
            }
            else if ((i+j)%2==1)   //左下
            {
                i++;
                j--;
            }
        }
    }
    cout << endl << "经过Z字形编排后的矩阵如下：" << endl;
    for (int i = 0; i < SIZE;i++)
    {
        for (int j = 0; j < SIZE;j++)
        {
            cout << setw(4) << *(*(a + i) + j);
        }
        cout << endl;
    }
    return 0;
}

 

运行结果：

原始矩阵如下：
   0   1   2   3   4   5   6   7
   8   9  10  11  12  13  14  15
  16  17  18  19  20  21  22  23
  24  25  26  27  28  29  30  31
  32  33  34  35  36  37  38  39
  40  41  42  43  44  45  46  47
  48  49  50  51  52  53  54  55
  56  57  58  59  60  61  62  63

经过Z字形编排后的矩阵如下：
   0   1   5   6  14  15  27  28
   2   4   7  13  16  26  29  42
   3   8  12  17  25  30  41  43
   9  11  18  24  31  40  44  53
  10  19  23  32  39  45  52  54
  20  22  33  38  46  51  55  60
  21  34  37  47  50  56  59  61
  35  36  48  49  57  58  62  63
请按任意键继续. . .

  以前也看过左神的课：里面有矩阵的各种方法遍历，自己也练习过：矩阵的操作