poj1901-求区间第k大值（带修改）树状数组套主席树

Posted 2020-08-17 Konjak谷弱

901: Zju2112 Dynamic Rankings

Time Limit: 10 Sec  Memory Limit: 128 MB
Submit: 7025  Solved: 2925
[Submit][Status][Discuss]

Description

给定一个含有n个数的序列a[1],a[2],a[3]……a[n]，程序必须回答这样的询问：对于给定的i,j,k，在a[i],a[i+1],a[i+2]……a[j]中第k小的数是多少(1≤k≤j-i+1)，并且，你可以改变一些a[i]的值，改变后，程序还能针对改变后的a继续回答上面的问题。你需要编一个这样的程序，从输入文件中读入序列a，然后读入一系列的指令，包括询问指令和修改指令。对于每一个询问指令，你必须输出正确的回答。 第一行有两个正整数n(1≤n≤10000)，m(1≤m≤10000)。分别表示序列的长度和指令的个数。第二行有n个数，表示a[1],a[2]……a[n]，这些数都小于10^9。接下来的m行描述每条指令，每行的格式是下面两种格式中的一种。 Q i j k 或者 C i t Q i j k （i,j,k是数字，1≤i≤j≤n, 1≤k≤j-i+1）表示询问指令，询问a[i]，a[i+1]……a[j]中第k小的数。C i t (1≤i≤n，0≤t≤10^9)表示把a[i]改变成为t。

Input

对于每一次询问，你都需要输出他的答案，每一个输出占单独的一行。

Output

 

Sample Input

5 3
3 2 1 4 7
Q 1 4 3
C 2 6
Q 2 5 3

Sample Output

3
6

HINT

 

20%的数据中，m,n≤100; 40%的数据中，m,n≤1000; 100%的数据中，m,n≤10000。

 

-------------------------------------------------------------------------------------

嗷嗷嗷A了好海森

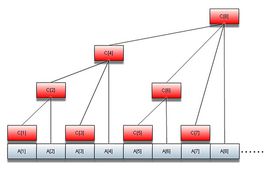
首先要回忆一下树状数组的样子。。它是一棵树的结构，也就是一个点只会被另一个点所访问到（父亲只有一个）。

上一题不带修改的主席树中，每一棵树是维护前缀区间1~L的。

这样，要是我们要修改一个数的话，就要把后面的主席树全部修改了。。复杂度变成了m*n*logn，这是不能接受的。

然后大神们就想到了树状数组！

我们修改每一棵主席树维护的区间，对于第i棵主席树，维护树状数组中所对应的lowbit(i)个数。

然后修改就只需要m*logn*logn了。

查询则变成了logn*logn的了。

 

  1 #include<cstdio>
  2 #include<cstdlib>
  3 #include<cstring>
  4 #include<cmath>
  5 #include<iostream>
  6 #include<algorithm>
  7 using namespace std;
  8 
  9 const int N=10010,INF=(int)1e9+100;
 10 int n,m,pl,tl,mx;
 11 int a[2*N],num[2*N],crt[2*N],root[2*N];
 12 char s[10];
 13 struct trnode{
 14     int lc,rc,cnt;
 15 }t[300*N];
 16 struct ques{
 17     int l,r,k,x,d;
 18     bool tmp;
 19 }q[N];
 20 struct node{
 21     int d,id;
 22 }p[2*N];
 23 
 24 bool cmp(node x,node y){return x.d<y.d;}
 25 
 26 int bt(int l,int r)
 27 {
 28     int x=++tl;
 29     t[x].cnt=0;
 30     t[x].lc=t[x].rc=0;
 31     if(l<r)
 32     {
 33         int mid=(l+r)/2;
 34         t[x].lc=bt(l,mid);
 35         t[x].rc=bt(mid+1,r);
 36     }
 37     return x;
 38 }
 39 
 40 int update(int rt,int p,int d)
 41 {
 42     int now=++tl,tmp=now;
 43     int l=1,r=mx,mid;
 44     t[now].cnt=t[rt].cnt+d;
 45     while(l<r)
 46     {
 47         mid=(l+r)/2;
 48         if(p<=mid)
 49         {
 50             r=mid;
 51             t[now].lc=++tl;
 52             t[now].rc=t[rt].rc;
 53             rt=t[rt].lc;
 54             now=tl;
 55         }
 56         else 
 57         {
 58             l=mid+1;
 59             t[now].lc=t[rt].lc;
 60             t[now].rc=++tl;
 61             rt=t[rt].rc;
 62             now=tl;
 63         }
 64         t[now].cnt=t[rt].cnt+d;
 65     }
 66     return tmp;
 67 }
 68 
 69 void add(int x,int p,int d)
 70 {
 71     for(int i=x;i<=n;i+=(i&(-i))) root[i]=update(root[i],p,d);
 72 }
 73 
 74 int getsum(int x)
 75 {
 76     int ans=0;
 77     for(int i=x;i>=1;i-=(i&(-i))) ans+=t[t[crt[i]].lc].cnt;
 78     return ans;
 79 }
 80 
 81 int query(int lx,int rx,int k)
 82 {
 83     for(int i=lx-1;i>=1;i-=(i&(-i))) crt[i]=root[i];//多棵树同时走。
 84     for(int i=rx;i>=1;i-=(i&(-i))) crt[i]=root[i];
 85     int l=1,r=mx,mid,sum;
 86     while(l<r)
 87     {
 88         mid=(l+r)/2;
 89         sum=getsum(rx)-getsum(lx-1);
 90         if(sum>=k)
 91         {
 92             r=mid;
 93             for(int i=lx-1;i>=1;i-=(i&(-i))) crt[i]=t[crt[i]].lc;
 94             for(int i=rx;i>=1;i-=(i&(-i))) crt[i]=t[crt[i]].lc;
 95         }
 96         else
 97         {
 98             l=mid+1;
 99             k-=sum;
100             for(int i=lx-1;i>=1;i-=(i&(-i))) crt[i]=t[crt[i]].rc;
101             for(int i=rx;i>=1;i-=(i&(-i))) crt[i]=t[crt[i]].rc;
102         }
103     }
104     return l;
105 }
106 
107 int main()
108 {
109     freopen("a.in","r",stdin);
110     scanf("%d%d",&n,&m);
111     pl=n;tl=0;
112     for(int i=1;i<=n;i++) 
113     {
114         scanf("%d",&a[i]);
115         p[i].d=a[i];p[i].id=i;
116     }
117     for(int i=1;i<=m;i++)
118     {
119         scanf("%s",s);
120         if(s[0]==\'Q\') 
121         {
122             q[i].tmp=0;
123             scanf("%d%d%d",&q[i].l,&q[i].r,&q[i].k);
124         }
125         else 
126         {
127             q[i].tmp=1;
128             scanf("%d%d",&q[i].x,&q[i].d);
129             p[++pl].d=q[i].d;p[pl].id=n+i;
130         }
131     }
132     sort(p+1,p+1+pl,cmp);
133     mx=0;p[0].d=INF;
134     for(int i=1;i<=pl;i++)
135     {
136         if(p[i].d!=p[i-1].d) mx++,num[mx]=p[i].d;
137         if(p[i].id<=n) a[p[i].id]=mx;
138         else q[p[i].id-n].d=mx;
139     }
140     // for(int i=1;i<=n;i++) printf("%d ",a[i]);printf("\\n");
141     root[0]=bt(1,mx);
142     for(int i=1;i<=n;i++) 
143         root[i]=root[0];
144     for(int i=1;i<=n;i++) 
145         add(i,a[i],1);
146     for(int i=1;i<=m;i++)
147     {
148         if(q[i].tmp==0)
149             printf("%d\\n",num[query(q[i].l,q[i].r,q[i].k)]);
150         else
151         {
152             add(q[i].x,a[q[i].x],-1);
153             add(q[i].x,q[i].d,1);
154             a[q[i].x]=q[i].d;//debug
155         }
156     }
157     return 0;
158 }