NOIp 2014 #2 联合权值 Label：图论 ！！！未AC

Posted 2020-08-16 Radiumlrb

题目描述

无向连通图G 有n 个点，n - 1 条边。点从1 到n 依次编号，编号为 i 的点的权值为W i ，每条边的长度均为1 。图上两点( u , v ) 的距离定义为u 点到v 点的最短距离。对于图G 上的点对( u, v) ，若它们的距离为2 ，则它们之间会产生Wu

×Wv 的联合权值。

请问图G 上所有可产生联合权值的有序点对中，联合权值最大的是多少？所有联合权值之和是多少？

输入输出格式

输入格式：

 

输入文件名为link .in。

第一行包含1 个整数n 。

接下来n - 1 行，每行包含 2 个用空格隔开的正整数u 、v ，表示编号为 u 和编号为v 的点之间有边相连。

最后1 行，包含 n 个正整数，每两个正整数之间用一个空格隔开，其中第 i 个整数表示图G 上编号为i 的点的权值为W i 。

 

输出格式：

 

输出文件名为link .out 。

输出共1 行，包含2 个整数，之间用一个空格隔开，依次为图G 上联合权值的最大值

和所有联合权值之和。由于所有联合权值之和可能很大，[b]输出它时要对10007 取余。 [/b]

 

输入输出样例

输入样例#1：

5  
1 2  
2 3
3 4  
4 5  
1 5 2 3 10 

输出样例#1：

20 74

说明

 

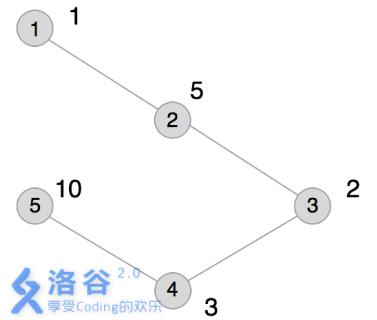
本例输入的图如上所示，距离为2 的有序点对有( 1,3) 、( 2,4) 、( 3,1) 、( 3,5) 、( 4,2) 、( 5,3) 。

其联合权值分别为2 、15、2 、20、15、20。其中最大的是20，总和为74。

【数据说明】

对于30% 的数据，1 < n≤ 100 ；

对于60% 的数据，1 < n≤ 2000；

 对于100%的数据，1 < n≤ 200 , 000 ，0 < wi≤ 10, 000 。

代码

 1 #include<iostream>
 2 #include<cstring>
 3 #include<cstdio>
 4 #include<algorithm>
 5 #include<vector>
 6 #include<map>
 7 #define MAXN 500005
 8 using namespace std;
 9 
10 struct cc{
11     map<int,int> m;
12 }nod[MAXN];
13 
14 int ans,sum,N;
15 int vis[MAXN],w[MAXN];
16 vector<int> G[MAXN];
17 
18 int cc(int x,int pre){
19     if(pre!=-1){
20         for(int i=0;i<G[pre].size();i++){
21             int pre_pre=G[pre][i];
22             if(pre_pre==x) continue;
23             if(nod[x].m.count(pre_pre)!=0) continue;
24             
25             nod[pre_pre].m[x]=nod[x].m[pre_pre]=1;
26             ans=max(ans,(w[pre_pre]*w[x])%10007);//注意题目描述，此处不应该取模
27             sum=(sum+w[pre_pre]*w[x]*2)%10007;
28 //            cout<<w[pre_pre]*w[x]<<endl;
29         }
30     }
31     vis[x]=1;
32 //    printf("%d %d %d \\n",x,pre,pre_pre);
33     for(int i=0;i<G[x].size();i++){
34         if(!vis[G[x][i]]) cc(G[x][i],x);
35     }
36 }
37 
38 int main(){
39 //    freopen("link.in","r",stdin);
40 //    freopen("link.out","w",stdout);
41     
42     scanf("%d",&N);
43     for(int i=1;i<N;i++){
44         int x,y;
45         scanf("%d%d",&x,&y);
46         G[x].push_back(y);
47         G[y].push_back(x);
48     }
49     for(int i=1;i<=N;i++) scanf("%d",&w[i]);
50     cc(1,-1);
51     printf("%d %d\\n",ans,sum);
52     return 0;
53 }

30分，脑洞map

 1 #include<iostream>
 2 #include<cstring>
 3 #include<cstdio>
 4 #include<algorithm>
 5 #include<vector>
 6 #include<map>
 7 #define MAXN 500005
 8 using namespace std;
 9 
10 int ans,sum,N;
11 int vis[MAXN],w[MAXN];
12 vector<int> G[MAXN];
13 
14 int cc(int x,int pre){
15     if(pre!=-1){
16         for(int i=0;i<G[pre].size();i++){
17             int pre_pre=G[pre][i];
18             if(pre_pre==x) continue;
19             if(!vis[pre_pre]) continue;
20             
21             ans=max(ans,w[pre_pre]*w[x]);//ans不用取模 
22             sum=(sum+w[pre_pre]*w[x]*2)%10007;
23         }
24     }
25     vis[x]=1;
26     for(int i=0;i<G[x].size();i++){
27         if(!vis[G[x][i]]) cc(G[x][i],x);
28     }
29 }
30 
31 int main(){
32 //    freopen("link.in","r",stdin);
33 //    freopen("link.out","w",stdout);
34     
35     scanf("%d",&N);
36     for(int i=1;i<N;i++){
37         int x,y;
38         scanf("%d%d",&x,&y);
39         G[x].push_back(y);
40         G[y].push_back(x);
41     }
42     for(int i=1;i<=N;i++) scanf("%d",&w[i]);
43     cc(1,-1);
44     printf("%d %d\\n",ans,sum);
45     return 0;
46 }

60分，还是TLE，大雾

 1 #include<iostream>
 2 #include<cstring>
 3 #include<cstdio>
 4 #include<algorithm>
 5 #include<vector>
 6 #define MAXN 500005
 7 using namespace std;
 8 
 9 int ans,sum,N;
10 int vis[MAXN],w[MAXN];
11 vector<int> G[MAXN];
12 
13 int cc(int x){
14     vis[x]=1;
15     if(G[x].size()>=2){
16         for(int i=0;i<G[x].size();i++){
17             for(int j=i+1;j<G[x].size();j++){
18                 int k=G[x][i],y=G[x][j];
19                 ans=max(ans,w[k]*w[y]);
20                 sum=(sum+w[k]*w[y]*2)%10007;
21             }
22         }
23     }
24 //    cout<<x<<endl;
25     for(int i=0;i<G[x].size();i++){
26         if(!vis[G[x][i]]) cc(G[x][i]);
27     }
28 }
29 
30 int main(){
31 //    freopen("link.in","r",stdin);
32 //    freopen("link.out","w",stdout);
33     
34     scanf("%d",&N);
35     for(int i=1;i<N;i++){
36         int x,y;
37         scanf("%d%d",&x,&y);
38         G[x].push_back(y);
39         G[y].push_back(x);
40     }
41     for(int i=1;i<=N;i++) scanf("%d",&w[i]);
42     cc(1);
43     printf("%d %d\\n",ans,sum);
44     return 0;
45 }

60分的另外一种写法

 

 

题解：//格式优化 by Radiumlrb

一、审题
首先我们一看到图就就知道图论有关，又因为有n个点和n-1条边，不难看出是一个无环图，这对题目的难度降低了很多。如果直接模拟的话肯定不行，会超时，所以我们应该换一种思维，及一个点周围的节点两两都能产生联合全值，
下面就来完善这一思想。

二、算法讨论
①、公式推导：
假如一个点x存在n个节点，分别为x1,x2…xn.
节点最大值只需存下节点中最大值，每次再用当前节点与最大节点相乘，在于max比较。
则关于x节点间的的联合全值之和为：
x（x2+x3…+xn）+x2(x1+x3…+xn)+xn(x1+x2…+xn-1) ；经整理可知就是每两个节点相乘，最后再成2即可；
化简为：
x1(x2+x3…+xn)+x2(x3+x4…+xn)+xn-2(xn-1+xn)+xn-1*xn
可理解为把每一个点和所有前面出现的的点之和相乘再相加最后乘2。

②、注意事项：
1、因为图是没有环的，所以一点到距离为二的点必定有且仅有一条，每一个点任意两个节点必将经过此点，所以我们不必讨论是否会重复。
2、因为数据范围很大，用邻接矩阵会爆内存，所以我们必须要用邻接矩阵才行(注意要存双向边）。
3、求联合权值之和时必须边做边对10007取模，不然会超出范围。

三、算法实现
用一个二维数组a存边，一维数组max1用来存该点节点中的最大值,大概就是这样吧，剩下的变量就在代码中一一解释。

四、代码展示

//Orz P党大神

 1 c,qz,dd:array[0..400000]of longint;  
 2 n,i,tot,x,y,max:longint;  
 3 //max存最大值，tot存联合全值之和  
 4 procedure sb(x:longint);  
 5 var i,tot1,nn,ny,max1:longint;  
 6 begin  
 7   tot1:=0; nn:=dd[x]; max1:=0;  
 8   ny:=a[nn].y; 
 9 //循环列举该点的所有节点  tot1存前面出现的节点全值之和。
10   repeat  
11     if max1*qz[ny]>max then max:=max1*qz[ny];  
12     if qz[ny]>max1 then max1:=qz[ny];  
13     tot:=(tot+tot1*(qz[ny]mod 10007))mod 10007;  
14 tot1:=(tot1+qz[ny])mod 10007;  
15 //要不断对10007取模
16     nn:=c[nn];  
17     ny:=a[nn].y;  
18   until nn=0;  
19 end;  
20 begin  
21 read(n);  
22 for i:=1 to n-1 do  
23    begin  
24 read(x,y);
25 a[i*2-1].x:=x;a[i*2-1].y:=y;
26 c[i*2-1]:=dd[x];dd[x]:=i*2-1;  
27 //此处为双向边  dd数组用来把起点相同的边绑定在一起
28 a[i*2].x:=y;  a[i*2].y:=x;   
29 c[i*2]:=dd[y];dd[y]:=i*2;  
30    end;  
31 for i:=1 to n do    
32     read(qz[i]);    
33 for i:=1 to n do  
34 sb(i);  
35 tot:=tot mod 10007;  
36 write(max,\' \',tot*2 mod 10007);  
37 //注意最后答案要乘2
38 end.  

 

五、最后的寄语：
其实本题还有更简单的做法，就是搜边即可，没必要枚举每个点，这个留给大家自己去想，我就不多讲。