动态规划---最长公共子序列

Posted 2020-08-16 akiradunn

1、问题描述
一个给定序列的子序列是在该序列中删去若干元素后得到的序列。确切的说，若给定序列X={x1,x2,…,xm}，则另一序列Z={z1,z2,…,zk}，X的子序列是指存在一个严格递增下标序列{i1,i2,…,ik}使得对于所有j=1,2,…k有zj=xij 例如,序列Z={B,C,D,B}是序列X={A,B,C,B,D,A,B}的子序列,相应的递增下标序列为{2,3,5,7}.
给定两个序列X和Y，当另一序列Z既是X的子序列又是Y的子序列时,称Z是序列X和Y的公共子序列,公共子序列可以有多个，最长公共子序列是X和Y序列的最长的一个.

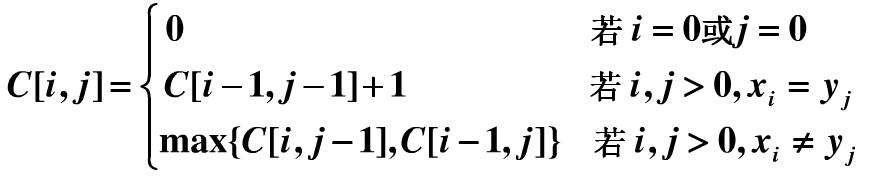
2、算法描述：
当xm =yn 时，找出Xm-1 和Yn-1 的最长公共子序列,然后在其尾部加上xm (=yn)即可得X和Y的最长公共子序列.当xm !=yn 时，必须解两个子问题，即找出Xm-1 和Y的一个最长公共子序列及X和Yn-1 的一个最长公共子序列。这两个公共子序列中较长者即为X和Y的最长公共子序列.

C[i][j]存储Xi和Yj的最长公共子序列的长度，from[i][j]代表C[i][j]长度所得来源于哪种情况;

3、算法时间复杂性分析
求解公共子序列的长度复杂度为m*n，根据存储状态表求子序列并输出复杂度为m*n，所以最终时间复杂度为m*n;

代码如下:

import java.util.Scanner;
public class LCS {
    public static void main(String[] args) {
        //ABCDEFGIE
        //BCDFGE
        Scanner input = new Scanner(System.in);
        String as = input.nextLine();
        String bs = input.nextLine();
        char [] a = as.toCharArray();
        char [] b = bs.toCharArray();
        int[][] from = init(a,b);
        comLength(a,b,from);
        //printArray(from);
        printCom(a,from,a.length-1,b.length-1);
    }
    public static void printArray(int[][] from){//输入给定数组将其打印
        for(int i=0; i<from.length ; i++){
            for(int j=0; j<from[0].length ; j++){
                System.out.print(from[i][j]+" ");
            }
            System.out.println();
        }
    }
    public static int[][] init(char[]a,char[]b){//创建来源数组
        int[][] from = new int[a.length][b.length];
        for(int i=0; i<a.length; i++){
            for(int j=0; j<b.length; j++){
                from[i][j]=0;
            }
        }
        return from;
    }
    public static void comLength(char[]a,char[]b,int[][]from){//为from状态数组赋值
         int m = a.length;
         int n = b.length;
         int [][]c = new int[m][n];
         for(int i=0; i<m; i++){
             for(int j=0; j<n; j++){
                 c[i][j]=0;
             }
         }
         for(int i=1; i<m; i++){
             for(int j=1; j<n; j++){
                 if(a[i]==b[j]){//代表来源于第1种情况:比较的两个字符串的最后一位相等
                     c[i][j]=c[i-1][j-1]+1;
                     from[i][j]=1;
                 }else if(c[i][j-1]>=c[i-1][j]){//代表来源于第2种情况:比较的两个字符串的最后一位相等且最长公共子序列的最后一位不等于a数组字符序列的最后一位；
                     c[i][j]=c[i][j-1];
                     from[i][j]=2;
                 }else{//代表来源于第3种情况:比较的两个字符串的最后一位不相等且最长公共子序列的最后一位不等于b数组字符序列的最后一位；
                     c[i][j]=c[i-1][j];
                     from[i][j]=3;
                 }
             }
         }
//         printArray(c);
//         System.out.println();
    }
    public static void printCom(char[]a , int[][]from , int m ,int n){//根据from状态数组输出最长公共子序列
          if(m==0|n==0)return;
          if(from[m][n]==1){
                 printCom(a,from,m-1,n-1);
                 System.out.print(a[m]);
          }else if(from[m][n]==2){
              printCom(a,from,m,n-1);
          }else {
              printCom(a,from,m-1,n);
          }
    }
}

View Code