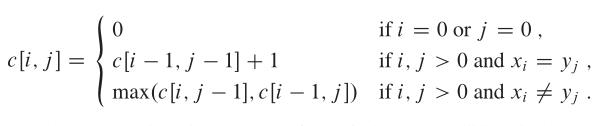算法导论—最长公共子序列(动态规划)
Posted 之墨_
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了算法导论—最长公共子序列(动态规划)相关的知识,希望对你有一定的参考价值。
算法导论—最长公共子序列((动态规划)
最长公共子序列
给定一个序列
X
=
<
x
1
,
x
2
,
x
3
,
x
4
.
.
.
,
x
m
>
X=<x_1,x_2,x_3,x_4...,x_m>
X=<x1,x2,x3,x4...,xm>,另一个序列
Z
=
<
z
1
,
z
2
,
z
3
,
z
4
.
.
.
,
z
k
>
Z=<z_1,z_2,z_3,z_4...,z_k>
Z=<z1,z2,z3,z4...,zk>,若存在一个严格递增的
X
X
X的下标序列
<
i
1
,
i
2
,
i
3
,
.
.
.
,
i
k
>
<i_1,i_2,i_3,...,i_k>
<i1,i2,i3,...,ik>对所有的
1
,
2
,
3
,
.
.
.
,
k
1,2,3,...,k
1,2,3,...,k,都满足
x
i
k
=
z
k
x_i_k=z_k
xik=zk,则称
Z
Z
Z是
X
X
X的子序列
注意这个子序列并不是一定要连续的,只是要相对位置不变
比如 Z = < B , C , D , B > Z=<B,C,D,B> Z=<B,C,D,B>是 X = < A , X=<A, X=<A, B \\largeB B, C \\largeC C , B , ,B, ,B, D \\largeD D , A , ,A, ,A, B \\largeB B > > >的子序列
公共子序列定义:
如果
Z
Z
Z既是
X
X
X的子序列,又是
Y
Y
Y的子序列,则称
Z
Z
Z为
X
X
X和
Y
Y
Y的公共子序列
最长公共子序列(以下简称LCS):
2个序列的子序列中长度最长的那个
定理
设 X = < x 1 , x 2 , x 3 , x 4 . . . , x m > , Y = < y 1 , y 2 , y 3 , y 4 . . . , y n > X=<x_1,x_2,x_3,x_4...,x_m>,Y=<y_1,y_2,y_3,y_4...,y_n> X=<x1,x2,x3,x4...,xm>,Y=<y1,y2,y3,y4...,yn>为两个序列, Z = < z 1 , z 2 , z 3 , z 4 . . . , z k > Z=<z_1,z_2,z_3,z_4...,z_k> Z=<z1,z2,z3,z4...,zk>是他们的任意 L C S LCS LCS。
- 如果 x m = y n x_m = y_n xm=yn,则 z k = x m = y n z_k = x_m = y_n zk=xm=yn 且 Z k − 1 Z_k-1 Zk−1是 X m − 1 X_m-1 Xm−1和 Y n − 1 Y_n-1 Yn−1的一个 L C S LCS LCS
- 如果 x m ≠ y n x_m ≠ y_n xm=yn 且 z k ≠ x m z_k ≠ x_m zk=xm,则 Z Z Z是 X m − 1 X_m-1 Xm−1和 Y Y Y的一个 L C S LCS LCS
- 如果 x m ≠ y n x_m ≠y_n xm=yn 且 z k ≠ y n z_k ≠ y_n zk=yn,则 Z Z Z是 X X X和 Y n − 1 Y_n-1 Yn−1的一个 L C S LCS LCS
递推式