最长公共子序列_动态规划

Posted 2021-01-25 henuliulei

具体问题的描绘和分析如下

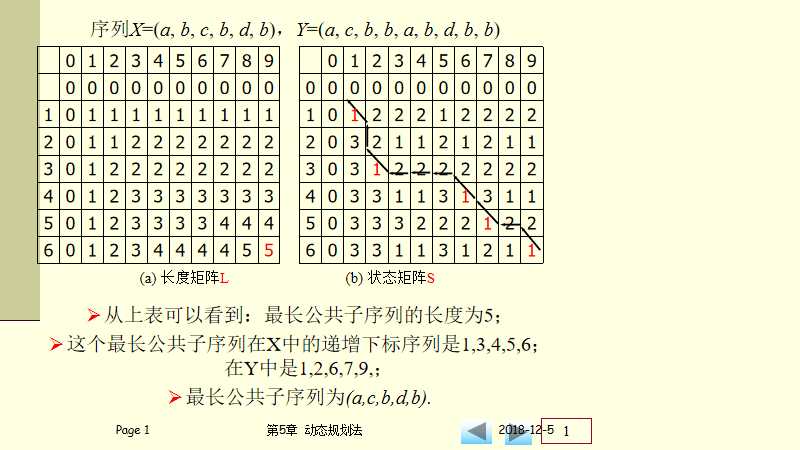
从上图可知，要构造两个二维数组，数组L用来求各种取值的子最长公共子序列，则最后一个元素就是最长公共子序列的长度，从右边的二维表，数值为1，则就是公共的元素，我们用数组记录下来，

代码如下：

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 int Maxson(int m,int n,char array[],char array1[],int L[][100],int s[][100],char z[])
 4 {
 5 
 6     for(int i=0;i<=m;i++){// //初始化第0行
 7 
 8         L[i][0]=0;
 9     }
10      for(int j=0;j<=n;j++){// //初始化第0列
11         L[0][j]=0;
12     }
13     for(int i=1;i<=m;i++){
14         for(int j=1;j<=n;j++){
15             if(array1[j]==array[i]){//式子（1）对应的代码
16                 L[i][j]=L[i-1][j-1]+1;
17                 s[i][j]=1;
18             }else{//式子（2）对应的代码
19                L[i][j]=max(L[i][j-1],L[i-1][j]);
20                if(L[i][j-1]>=L[i-1][j]){
21                 s[i][j]=2;
22                }
23                else{
24                 s[i][j]=3;
25                }
26             }
27         }
28     }
29     int i=m;
30     int j=n;
31     int k=L[m][n];
32     while(i>0&&j>0){//从二维数组s里面得到公共子序列的元素
33         if(s[i][j]==1){
34             z[k]=array[i]; k--; i--; j--;
35         }
36           else if (s[i][j]==2) j--;
37                else i--;
38 
39     }
40     return L[m][n];
41 }
42 int main()
43 {
44     int m;
45     cout << "请输入第一个序列的元素的个数" << endl;
46     cin >> m;
47     cout << "请输入第一个序列的每个元素" << endl;
48     char array[m+1];
49 
50     for(int i=1;i<=m;i++){
51         cin >> array[i];
52     }
53     int n;
54     cout << "请输入第二个序列的元素的个数" << endl;
55     cin >> n;
56     cout << "请输入第二个序列的每个元素" << endl;
57     char array1[n+1];
58     for(int i=1;i<=n;i++){
59         cin >> array1[i];
60     }
61     int L[m+1][100];
62     int s[m+1][100];
63     memset(L,0,sizeof(L));
64     memset(s,0,sizeof(s));
65     char z[100];
66     memset(z,0,sizeof(z));
67     cout <<"公共子序列长度是" <<Maxson(m,n,array,array1,L,s,z)<< endl;
68     cout << " 公共子序列是"<< endl;
69     for(int i=1;i<=n;i++){
70        cout << z[i]<< " ";
71     }
72     return 0;
73 }

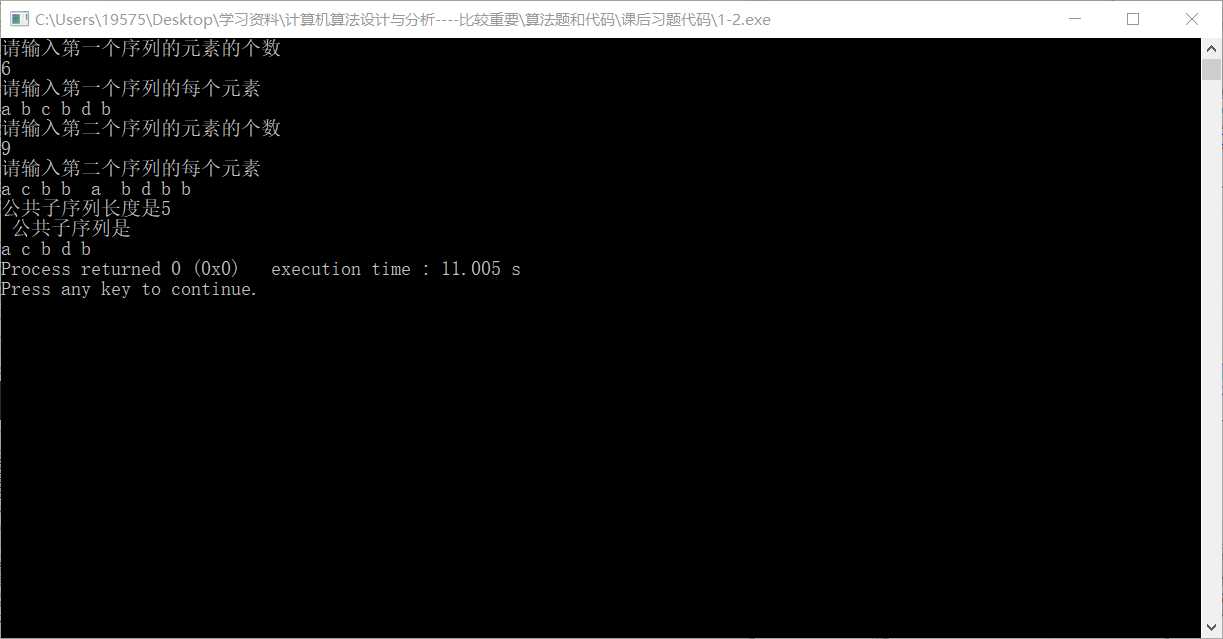
运行结果如下：