决策树

Posted 2020-08-15 Michael2397

决策树原理

0. 机器学习中分类和预测算法的评估：

• 准确率
• 速度
• 强壮行
• 可规模性
• 可解释性

1. 什么是决策树/判定树（decision tree)?

     

     判定树是一个类似于流程图的树结构：其中，每个内部结点表示在一个属性上的测试，每个分支代表一个属性输出，而每个树叶结点代表类或类分布。树的最顶层是根结点。

 

 

 

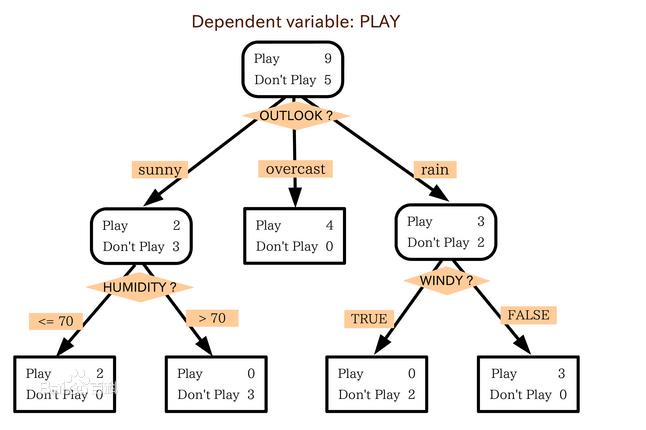
2.  机器学习中分类方法中的一个重要算法

 

3.  构造决策树的基本算法     

 

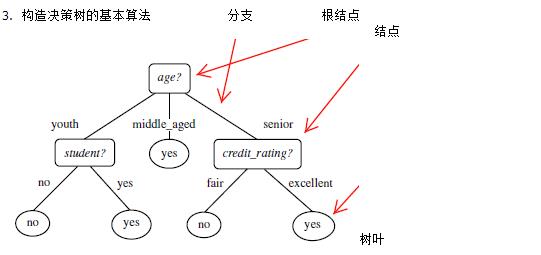
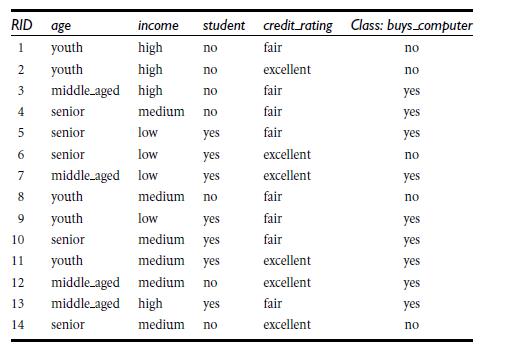
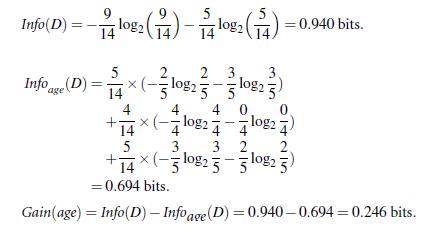
 类似，Gain(income) = 0.029, Gain(student) = 0.151, Gain(credit_rating)=0.048

 

          所以，选择age作为第一个根节点

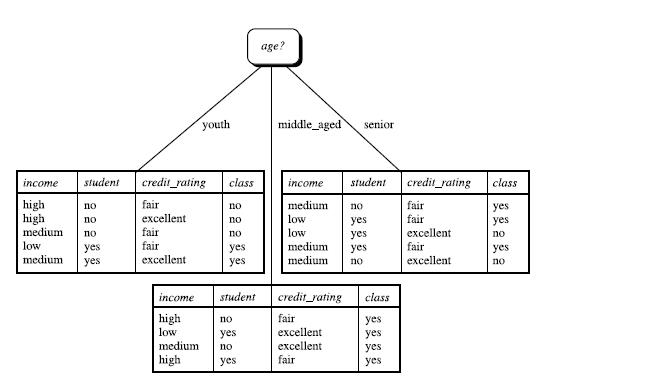
  重复。。。

 

 

          算法：

• 树以代表训练样本的单个结点开始（步骤1）。
• 如果样本都在同一个类，则该结点成为树叶，并用该类标号（步骤2 和3）。
• 否则，算法使用称为信息增益的基于熵的度量作为启发信息，选择能够最好地将样本分类的属性（步骤6）。该属性成为该结点的“测试”或“判定”属性（步骤7）。在算法的该版本中，
• 所有的属性都是分类的，即离散值。连续属性必须离散化。
• 对测试属性的每个已知的值，创建一个分枝，并据此划分样本（步骤8-10）。
• 算法使用同样的过程，递归地形成每个划分上的样本判定树。一旦一个属性出现在一个结点上，就不必该结点的任何后代上考虑它（步骤13）。
• 递归划分步骤仅当下列条件之一成立停止：
• (a) 给定结点的所有样本属于同一类（步骤2 和3）。
• (b) 没有剩余属性可以用来进一步划分样本（步骤4）。在此情况下，使用多数表决（步骤5）。
• 这涉及将给定的结点转换成树叶，并用样本中的多数所在的类标记它。替换地，可以存放结
• 点样本的类分布。
• (c) 分枝
• test_attribute = a i 没有样本（步骤11）。在这种情况下，以 samples 中的多数类
• 创建一个树叶（步骤12）

 

               

 

 

     3.1 其他算法：

               C4.5:  Quinlan

               Classification and Regression Trees (CART): (L. Breiman, J. Friedman, R. Olshen, C. Stone)

               共同点：都是贪心算法，自上而下(Top-down approach)

               区别：属性选择度量方法不同： C4.5 （gain ratio), CART(gini index), ID3 (Information Gain)

 

     3.2 如何处理连续性变量的属性？ 

 

4. 树剪枝叶 （避免overfitting)

     4.1 先剪枝

     4.2 后剪枝

 

 

5. 决策树的优点：

     直观，便于理解，小规模数据集有效     

 

6. 决策树的缺点：

     处理连续变量不好

     类别较多时，错误增加的比较快

     可规模性一般（