洛谷⑨月月赛Round2 P3393逃离僵尸岛[最短路]

Posted 2020-08-10 Candy?

题目描述

小a住的国家被僵尸侵略了！小a打算逃离到该国唯一的国际空港逃出这个国家。

该国有N个城市，城市之间有道路相连。一共有M条双向道路。保证没有自环和重边。

K个城市已经被僵尸控制了，如果贸然闯入就会被感染TAT...所以不能进入。由其中任意城市经过不超过S条道路就可以到达的别的城市，就是危险城市。换句话说只要某个没有被占城市到某个被占城市不超过s距离，就是危险。

小a住在1号城市，国际空港在N号城市，这两座城市没有被侵略。小a走每一段道路（从一个城市直接到达另外一个城市）得花一整个白天，所以晚上要住旅店。安全的的城市旅馆比较便宜要P元，而被危险的城市，旅馆要进行安保措施，所以会变贵，为Q元。所有危险的城市的住宿价格一样，安全的城市也是。在1号城市和N城市，不需要住店。

小a比较抠门，所以他希望知道从1号城市到N号城市所需要的最小花费。

输入数据保证存在路径，可以成功逃离。输入数据保证他可以逃离成功。

输入输出格式

输入格式：

 

第一行4个整数(N,M,K,S)

第二行2个整数(P,Q)

接下来K行，ci，表示僵尸侵占的城市

接下来M行，ai,bi，表示一条无向边

 

输出格式：

 

一个整数表示最低花费

 

输入输出样例

输入样例#1：

13 21 1 1
1000 6000
7
1 2
3 7
2 4
5 8
8 9
2 5
3 4
4 7
9 10
10 11
5 9
7 12
3 6
4 5
1 3
11 12
6 7
8 11
6 13
7 8
12 13

输出样例#1：

11000

说明

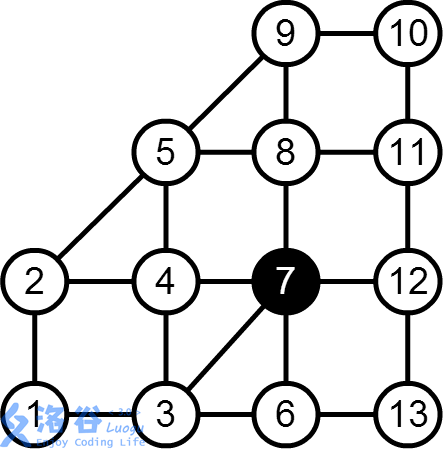
对于20%数据，N<=50

对于100%数据，2 ≦ N ≦ 100000, 1 ≦ M ≦ 200000, 0 ≦ K ≦ N - 2, 0 ≦ S ≦ 100000

1 ≦ P ＜ Q ≦ 100000

---

 

很明显先预处理有无危险，然后就是最短路问题

因为是点权图，我yy了一个拆点多做法，结果不知道哪里写错了就对了一个点

原来可以把点权分给边，可以把终点的点权分给这条边

预处理每个僵尸的城市往外bfs就可以了，只要加之前判一下vis就不会超时，当时还想了好多奇葩的优化.....

spfa比dijkstra快了100多ms

//
//  main.cpp
//  luogu9.2.2
//
//  Created by Candy on 9/24/16.
//  Copyright © 2016 Candy. All rights reserved.
//

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<queue>
using namespace std;
typedef long long ll;
const int N=1e5+5,M=2e5+5;
int read(){
    char c=getchar();int x=0,f=1;
    while(c<‘0‘||c>‘9‘){if(c==‘-‘)f=-1; c=getchar();}
    while(c>=‘0‘&&c<=‘9‘){x=x*10+c-‘0‘; c=getchar();}
    return x*f;
}
struct edge{
    int v,ne;
}e[M<<1];
int h[N],cnt=0;
void ins(int u,int v){
    cnt++;
    e[cnt].v=v;e[cnt].ne=h[u];h[u]=cnt;
    cnt++;
    e[cnt].v=u;e[cnt].ne=h[v];h[v]=cnt;
}
int n,m,k,s,P,Q,tmp,u,v;
int z[N],pw[N],lst[N];
struct hn{
    int u;ll d;
    bool operator <(const hn &rhs)const{return d>rhs.d;}
    hn(int a=0,ll b=0):u(a),d(b){}
};
int vis[N];
void bfs(int S){
    memset(vis,0,sizeof(vis));
    queue<hn> q;
    q.push(hn(S,0));
    vis[S]=1;
    while(!q.empty()){
        hn x=q.front();q.pop();
        int u=x.u;ll d=x.d;
        if(d==s) continue;
        for(int i=h[u];i;i=e[i].ne){
            int v=e[i].v;
            if(vis[v]) continue;
            vis[v]=1;
            pw[v]=Q;
            q.push(hn(v,d+1));
        }
    }
}
ll d[N]; bool done[N];
void dijkstra(int S){
    memset(d,127,sizeof(d));
    priority_queue<hn> q;
    q.push(hn(S,0));
    d[S]=0;
    while(!q.empty()){
        hn x=q.top();q.pop();
        int u=x.u;
        if(done[u]) continue;
        done[u]=1;
        for(int i=h[u];i;i=e[i].ne){
            int v=e[i].v,w=pw[v];
            if(z[v]) continue;
            if(d[v]>d[u]+w){
                d[v]=d[u]+w;
                q.push(hn(v,d[v]));
            }
        }
    }
}
bool inq[N];
void spfa(){
    memset(d,127,sizeof(d));
    queue<int> q;
    q.push(1);inq[1]=1;d[1]=0;
    while(!q.empty()){
        int u=q.front();q.pop();inq[u]=0;
        for(int i=h[u];i;i=e[i].ne){
            int v=e[i].v;ll w=pw[v];
            if(z[v]) continue;
            if(d[v]>d[u]+w){
                d[v]=d[u]+w;
                if(!inq[v]){inq[v]=1;q.push(v);}
            }
        }
    }
}
int main(int argc, const char * argv[]) {
    n=read();m=read();k=read();s=read();P=read();Q=read();
    for(int i=1;i<=k;i++) {lst[i]=read();z[lst[i]]=1;}
    for(int i=1;i<=m;i++) {u=read();v=read();ins(u,v);}
    
    for(int i=1;i<=n;i++) pw[i]=P;
    for(int i=1;i<=k;i++) bfs(lst[i]);
    pw[n]=0;
    dijkstra(1);
    //spfa();
    printf("%lld",d[n]);
    return 0;
}