动态规划（最大公共子序列）

Posted 2020-08-09 知晓的老巢

网上关于动态规划的资料很多，看了很多，总结如下：

求原字符串和其反串的最大公共子序列（不是子串，因为可以不连续）的长度（使用动态规划很容易求得）　

1)首先是要知道最长公共子序列的长度的动态规划方程

　　　　设有字符串a[0...n]，b[0...m]，下面就是递推公式。字符串a对应的是二维数组num的行，字符串b对应的是二维数组num的列。

　　　　

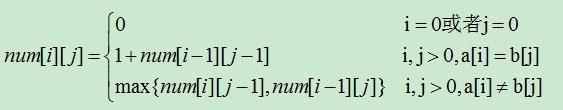
2、其次要看的懂求BDCABA与ABCBDAB的最大公共子序列

3、关键代码如下：

 1 package com.sxt.bean;
 2 
 3 import java.util.Scanner;
 4 
 5 public class Demo{
 6     public static void main(String[] args){
 7         Scanner scan = new Scanner(System.in);
 8         while(scan.hasNextLine()){
 9             String str = scan.nextLine();
10             String revStr = reverse(str);
11             int lcs = getLongestCommonSeq(str, revStr);
12             System.out.println(str.length()-lcs);
13         }
14     }
15     public static int getLongestCommonSeq(String str1, String str2){
16         int len1 = str1.length();
17         int len2 = str2.length();
18        
19         int[][] c = new int[len1+1][len2+1];
20         for(int i=0; i<=len1; i++){
21             c[i][0] = 0;
22         }
23         for(int j=0; j<=len2; j++){
24             c[0][j] = 0;
25         }
26         for(int i=1; i<=len1; i++){
27             for(int j=1; j<=len2; j++){
28                 char char1 = str1.charAt(i-1);
29                 char char2 = str2.charAt(j-1);
30                 if(char1 == char2){
31                     c[i][j] = c[i-1][j-1]+1;
32                 }else{
33                     c[i][j] = max(c[i][j-1], c[i-1][j]);
34                 }
35                 System.out.print(c[i][j]+" ");
36             }
37             System.out.println();
38         }
39         //打印出公共子序列
40         char str[]= new char[100];
41         int index = c[len1][len2]-1;
42         System.out.print("子字符串为：");
43         for (int i = len1,j = len2; i>0&&j>0;)
44         {
45             if(str1.charAt(i-1) == str2.charAt(j-1))
46             {
47                 str[index--] = str1.charAt(i-1);
48                 i--;
49                 j--;
50                 System.out.print(str1.charAt(i));
51             }
52             else 
53             {
54                 if(c[i][j-1]>c[i-1][j])
55                 {
56                     j--;
57                 }else 
58                 {
59                     i--;
60                 }
61             }
62         }
63         System.out.println();
64         return c[len1][len2];
65     }
66  
67     public static int max(int i1, int i2){
68         if(i1 > i2) return i1;
69         else return i2;
70     }
71  
72     public static String reverse(String str){
73         String reverseStr = "";
74         for(int i=str.length()-1; i>=0; i--){
75             reverseStr += str.charAt(i);
76         }
77         return reverseStr;
78     }
79 }

参考资料：http://www.cnblogs.com/newpanderking/p/3946159.html