最长公共子序列-递归.动态规划

Posted 2021-10-07 nuist__NJUPT

最长公共子序列-递归

给出两个字符串，求出这样的一个最长的公共子序列的长度,而且每个字符的先后顺序和原串中的先后顺序一致,可以不相离

输入值

输入中的每行由两个由空格分隔开得字符串

输出量

每组数据，输出最大长度

样本输入
abcfbc abfcab
programming contest
abcd mnp

样本输出
4
2
0

方法一：递归，以s1的第1个字符开头，依次与s2的各个字符对比，若找到第一个相等，则其余递归求出，并退出当前循环，然后以s1的第2个字符开头，依次与s2的各个字符对比，依次类推，找到最大的公共子序列。

import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;

public class LCS {
    public static List<Character> dfs(String s1, String s2){
        int len1 = s1.length() ; //两个字符串的长度
        int len2 = s2.length() ;
        List<Character> res = new ArrayList<>() ; //存储最终的的结果集合
        for(int i=0; i<len1; i++){
            List<Character> ans = new ArrayList<>() ; //存储以i为开头的公共序列的字串
            for(int j=0; j<len2; j++){
                if(s1.charAt(i) == s2.charAt(j)){
                    ans.add(s1.charAt(i)) ; //添加当前相等的字符
                    ans.addAll(dfs(s1.substring(i+1), s2.substring(j+1))) ; //剩余的字符串递归求解
                    break ;
                }
            }
            if(ans.size() > res.size()){ //如果更大的公共子序列，则更新
                res = ans ;
            }
        }
        return res ;
    }
    public static void main(String[] args) {
        Scanner input = new Scanner(System.in) ;
        while(true) {
            String s1 = input.next();
            String s2 = input.next();
            List<Character> list = dfs(s1, s2);
            System.out.println(list.size());
        }
    }
}

方法2：动态规划
dp状态转移方程式如下：

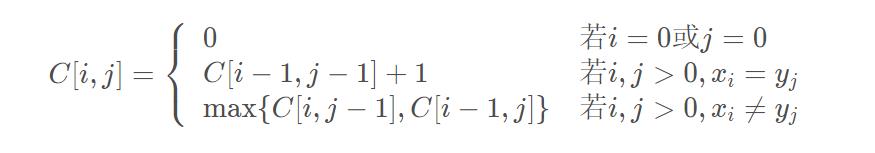
import java.util.Scanner;

public class LCS {
    public static void f(String s1, String s2){
        int len1 = s1.length() ;
        int len2 = s2.length() ;
        int [][] dp = new int [len1+1][len2+1] ;
        for(int i=0; i<len2+1; i++){
            dp[0][i] = 0 ;
        }
        for(int i=0; i<len1+1; i++){
            dp[i][0] = 0 ;
        }
        for(int i=1; i<len1+1; i++){
            for(int j=1; j<len2+1; j++){
                if(s1.charAt(i-1) == s2.charAt(j-1)){
                    dp[i][j] = dp[i-1][j-1] + 1 ;
                }else{
                    dp[i][j] = Math.max(dp[i][j-1], dp[i-1][j]) ;
                }
            }
        }
        System.out.println(dp[len1][len2]) ;
    }
    public static void main(String[] args){
        Scanner input = new Scanner(System.in) ;
        while(true){
            String s1 = input.next() ;
            String s2 = input.next() ;
            f(s1, s2) ;
        }
    }
}