矩阵的迹(转)
Posted 川师15级软工研=雁=
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了矩阵的迹(转)相关的知识,希望对你有一定的参考价值。
矩阵的迹
在线性代数中,一个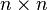 的矩阵
的矩阵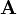 的迹(或迹数),是指
的迹(或迹数),是指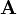 的主对角线(从左上方至右下方的对角线)上各个元素的总和,一般记作
的主对角线(从左上方至右下方的对角线)上各个元素的总和,一般记作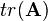 或
或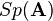 :
:
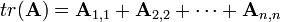
其中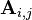 代表矩阵的第i行j列上的元素的值[1]。一个矩阵的迹是其特征值的总和(按代数重数计算)。
代表矩阵的第i行j列上的元素的值[1]。一个矩阵的迹是其特征值的总和(按代数重数计算)。
迹的英文为trace,是来自德文中的Spur这个单字(与英文中的Spoor是同源词),在数学中,通常简写为“Sp”或“tr”。
设有矩阵:
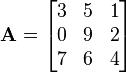
它的迹是:
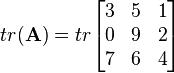 = 3 + 9 + 4 = 16
= 3 + 9 + 4 = 16
给定一个环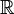 ,迹是一个从系数在环中的
,迹是一个从系数在环中的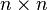 矩阵的空间
矩阵的空间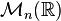 射到环
射到环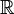 之上的线性算子。也就是说,对于任两个
之上的线性算子。也就是说,对于任两个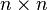 的矩阵
的矩阵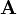 、
、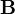 和标量
和标量 ,都有:
,都有:
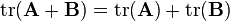
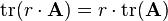 [2]
[2]
更进一步来说,当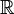 是一个域时,迹数函数
是一个域时,迹数函数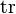 是
是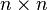 矩阵的空间
矩阵的空间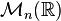 上的一个线性泛函。
上的一个线性泛函。
由于一个矩阵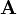 的转置矩阵
的转置矩阵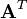 的主对角线元素和原来矩阵的主对角线元素是一样的,所以任意一个矩阵和其转置矩阵都会有相同的迹[2]:
的主对角线元素和原来矩阵的主对角线元素是一样的,所以任意一个矩阵和其转置矩阵都会有相同的迹[2]:
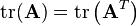 矩阵乘积的迹数
矩阵乘积的迹数
设A是一个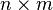 矩阵,B是个
矩阵,B是个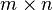 矩阵,则:
矩阵,则:
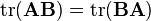 [2]
[2]
其中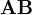 是一个
是一个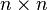 矩阵,而
矩阵,而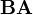 是一个
是一个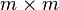 矩阵。
矩阵。
上述的性质可以由矩阵乘法的定义证明:
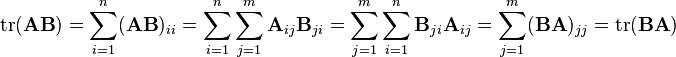
如果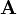 都是
都是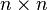 的方形矩阵,那么它们的乘积
的方形矩阵,那么它们的乘积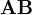 和
和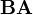 也会是方形矩阵。因此,利用这个结果,可以推导出:计算若干个同样大小的方形矩阵的乘积的迹数时,可以循环改变乘积中方形矩阵相乘的顺序,而最终的结果不变</math>[2]。例如,有三个方形矩阵
也会是方形矩阵。因此,利用这个结果,可以推导出:计算若干个同样大小的方形矩阵的乘积的迹数时,可以循环改变乘积中方形矩阵相乘的顺序,而最终的结果不变</math>[2]。例如,有三个方形矩阵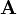 、
、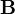 和
和 ,则:
,则:
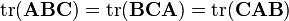 [3]
[3]
但是要注意:
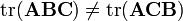 [3]
[3]
更一般地,乘积中的矩阵不一定要是方形矩阵,只要某一个循环改变后的乘积依然存在,那么得到的迹数依然会和原来的迹数相同[2]。
另外,如果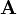 、
、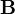 和
和 是同样大小的方阵而且还是对称矩阵的话,那么其乘积的迹数不只在循环置换下不会改变,而且在所有的置换下都不会改变:
是同样大小的方阵而且还是对称矩阵的话,那么其乘积的迹数不只在循环置换下不会改变,而且在所有的置换下都不会改变:
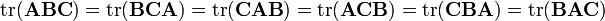
http://blog.sciencenet.cn/blog-357889-616860.html
以上是关于矩阵的迹(转)的主要内容,如果未能解决你的问题,请参考以下文章
矩阵的基本性质 之 正规矩阵,矩阵的迹,行列式,伴随矩阵,矩阵的逆,对角矩阵,矩阵求导