PGM：贝叶斯网表示之朴素贝叶斯模型naive Bayes

Posted 2020-08-07 -柚子皮-

http://blog.csdn.net/pipisorry/article/details/52469064

独立性质的利用

条件参数化和条件独立性假设被结合在一起，目的是对高维概率分布产生非常紧凑的表示。

随机变量的独立性

[PGM：概率论基础知识 ：独立性性质的利用]

条件参数化方法

Note: P(I), P(S | i0), P(S | i1)都是二项式分布，都只需要一个参数。

皮皮blog

朴素贝叶斯模型naive Bayes

朴素贝叶斯模型的学生示例

{这个示例很好的阐述了什么是朴素贝叶斯网络模型，后面将讲到其一般化模型和分类的应用实例}

问题描述

模型的因子表示

符号表示：I表示智商；S（AT）代表SAT成绩；G（rade）代表某些课程成绩。

如果我们知道一个学生是高智商的，那么他在SAT考试中获得的高分并不能为我们带来任何有关他课程成绩的信息。

Note: 这种表示中在3个二项式表示和2个三项式表示。

因子表示的优点

[概率图模型  原理与技术[（美）科勒，（以）弗里德曼著]

皮皮blog

朴素贝叶斯一般模型

朴素贝叶斯模型的一般化定义

给定类时特征条件独立

Note：对应上面的学生示例，就是说，当类变量C(示例中就是智商I)确定时，类的feature(示例中的Grade和SAT)之间就是独立的（其实就是贝叶斯网的tail-to-tail结构形式）。

朴素贝叶斯模型的贝叶斯网络：

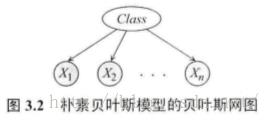
朴素贝叶斯模型的因子分解及参数

共2n+1个二项分布，需要2n+1个独立参数。

朴素贝叶斯参数个数与变量个数呈线性关系，而不像联合分布的显式表示中那样呈指数关系。

使用朴素贝叶斯模型进行分类

也就是说朴素贝叶斯分类器主要是训练参数p(c){每个独立的p(ci)}和p(x|c){每个独立的p(xi|ci)=num(xi=i, ci=i)/num(ci=i)}（这些参数可以通过训练数据是直接通过频率计算出来的（MLE方法）），通过取最大的p(c|new_x)来预测new_x的类别。

构建这种模型的强假设降低了模型诊断的准确性，尤其是过度计算某些特定的证据，该模型倾向于过高估计其影响。例如高血压和肥胖症是心脏疾病的两个硬指标，不过这两个症状相互之间高度相关。引发疾病证据被重复计算。

朴素贝叶斯分类算法的优缺点

优点：在数据较少的情况下依然有效，可以处理多类别问题

缺点：对输入数据的准备方式敏感

适用数据类型：标称型数据

    朴素贝叶斯方法不需要进行结构学习，建立网络结构非常简单，实验结果和实践证明，它的分类效果比较好。

但在实际的应用领域中，朴素贝叶斯网络分类器具有较强的限定条件即各个属性相互独立的假设很难成立。我们应该广义地理解这种独立性，即属性变量之间的条件独立性是指：属性变量之间的依赖相对于属性变量与类变量之间的依赖是可以忽略的，这就是为什么朴素贝叶斯网络分类器应用的最优范围比想象的要大得多的一个主要原因。朴素贝叶斯分类器以简单的结构和良好的性能受到人们的关注，它是最优秀的分类器之一。在理论上它在满足其限定条件下是最优的，但它有较强的限定条件，可以尝试减弱它的限定条件以扩大最优范围，产生更好的分类器。朴素贝叫斯分类器可以进行扩展为广义朴素贝叶斯分类器。

皮皮blog

朴素贝叶斯分类算法的实现

朴素贝叶斯分类算法的python实现

#!/usr/bin/env python
# -*- coding: utf-8 -*-
"""
__title__ = '朴素贝叶斯算法(亦适用于多类分类)'
__author__ = 'pika'
__mtime__ = '16-5-23'
__email__ = '[e-mail]'
# code is far away from bugs with the god animal protecting
    I love animals. They taste delicious.
"""
import numpy as np

TRAIN_FILE = r'./trainingData.txt'
TEST_FILE = r'./testingData.txt'


def train_naive_bayes(x, y):
    '''
    训练参数：p(c){包含每个独立的p(ci)}和p(x|c){包含每个独立的p(xi|ci)}
    '''
    p_c = {}  # p(c) = {ci : p(ci)}
    p_x_cond_c = {}  # p(x|c) = {ci : [p(xi|ci)]}
    for l in np.unique(y):
        # label l下， x=1 [xi = 1]时的概率array[p(xi=1|c=l)]; 则1-array[p(xi=1|c=l)]就是array[p(xi=0|c=l)]
        p_x_cond_c[l] = x[y == l].sum(0) / (y == l).sum()
        p_c[l] = (y == l).sum() / len(y)  # p(c=l)的概率
    print("θC: {}\\n".format(p_c))
    print("θA1=0|C: {}\\n".format({a[0]: 1 - a[1][0] for a in p_x_cond_c.items()}))
    print("θA1=1|C: {}\\n".format({a[0]: a[1][0] for a in p_x_cond_c.items()}))
    return p_c, p_x_cond_c


def predict_naive_bayes(p_c, p_x_cond_c, new_x):
    '''
    预测每个新来单个的x的label，返回一个label单值
    '''
    # new_x在类别l下的概率array
    p_l = [(l, p_c[l] * (np.multiply.reduce(p_x_cond_c[l] * new_x + (1 - p_x_cond_c[l]) * (1 - new_x)))) for l in
           p_c.keys()]
    p_l.sort(key=lambda x: x[1], reverse=True)  # new_x在类别l下的概率array按照概率大小排序
    return p_l[0][0]  # 返回概率最大对应的label


if __name__ == '__main__':
    tdata = np.loadtxt(TRAIN_FILE, dtype=int)
    x, y = tdata[:, 1:], tdata[:, 0]
    p_c, p_x_cond_c = train_naive_bayes(x, y)

    tdata = np.loadtxt(TEST_FILE, dtype=int)
    x, y = tdata[:, 1:], tdata[:, 0]
    predict = [predict_naive_bayes(p_c, p_x_cond_c, xi) for xi, yi in zip(x, y)]
    error = (y != predict).sum() / len(y)
    print("test error: {}\\n".format(error))

[机器学习经典算法详解及Python实现---朴素贝叶斯分类及其在文本分类、垃圾邮件检测中的应用]

from: http://blog.csdn.net/pipisorry/article/details/52469064

ref: [概率图模型  原理与技术[（美）科勒，（以）弗里德曼著]*