KMP算法简明扼要的理解

Posted 2020-08-06 繁星的技术博客

KMP算法也算是相当经典，但是对于初学者来说确实有点绕，大学时候弄明白过后来几年不看又忘记了，然后再弄明白过了两年又忘记了，好在之前理解到了关键点，看了一遍马上又能理解上来。关于这个算法的详解网上文章可以说遍地开花，可我觉得大多数文章，不需要看内容，光看看详解的文章篇幅就可以吓死人，然后讲来讲去内容也让人云里雾里。我在这里结合自己的理解，简单的解释一下。

在读这篇文章之前，首先请忘记以前了解的关于KMP算法的任何知识点。因为关于有些文章的解释还不一样，可能会让本来就很绕的说法变得更绕，与其说哪样还不如心中无一物一切归零重新开始。

然后来看一张图，这是两段字符暴力匹配的过程：

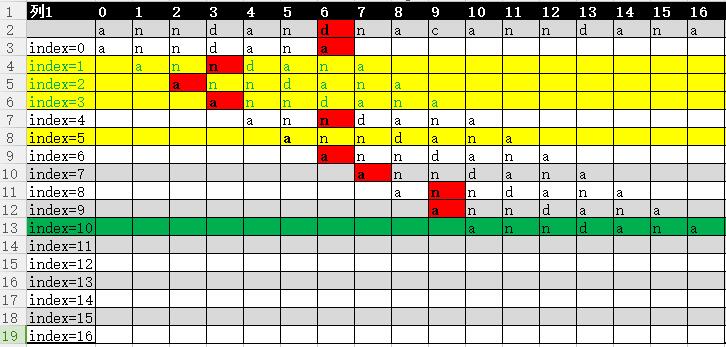
以上黄色部分是多余比较，红色是不匹配，绿色的匹配成功

目标字符串T：anndandnacanndana
匹配字符串P：anndana

匹配的时候匹配字符串从前到后移动了10次比较结束，最后得到确认结果。但是事实上图中黄色部分的比较是不需要的，也就是说如果利用KMP算法的特点，从中可以减少4次移动，从而会减少一些无意义的比较次数。那么问题来了，KMP算法为什么能减少这么多次比较次数呢？这究竟是有什么内部含义？

事实上,KMP算法就是典型的利用空间换时间，首先根据匹配字符串(annacanna) 特点，换算出来一张表（Next数组），每次移动多少根据表中的数据取值。

好吧，以上就是KMP的概要，归结起来也就是两条法则：

Next数组计算法则：对于任何字符串P的第n项(记为Pn)，此时的Next[n]为字符串P第n项之前的前缀和后缀共有字符串的最大长度。所谓前缀和后缀，就是分别除去首字符和末尾字符后的所有元素，然后取最大共有字符串的长度。

以anndana例：
1."a"的前缀和后缀都为空集，共有元素的长度为0；
2."an"的前缀为[a]，后缀为[n]，共有元素的长度为0；
3."ann"的前缀为[a, an]，后缀为[nn, n]，共有元素的长度0；
4."annd"的前缀为[a, an, ann]，后缀为[nnd, nn, d]，共有元素的长度为0；
5."annda"的前缀为[a, an, ann, annd]，后缀为[nnda, nda,da, a]，共有元素为"a"，长度为1；
6."anndan"的前缀为[a, an, ann, annd, annda]，后缀为[nndan, ndan, dan, an, a]，共有元素为"an","a"，但是长度为2；
7."anndana"的前缀为[a, an, ann, annd, annda, anndan]，后缀为[nndana, ndana, dana, ana, na, a]，共有元素“a”的长度为1。

移动法则：对于要比较的目标字符串T和匹配字符串P，首先利用匹配字符串P换算出来匹配移动表Next数组，然后匹配，当P(n)与T(m)不等的时候：
1) 如果n=0,则匹配字符串向右移动1位
2) 如果n>0 则取Next(n),向右移动整个匹配字符串直到P（Next(n)）与T（m）对其比较，可以说移动位数就是已匹配字符串长度-Next（n）。

那么结合上图理解

1.当index=0的时候，不匹配索引出现在6，因为next[6]=2，那么按照上面的法则，就应该讲P（2）与T（6）对其比较，于是需要将P移动5位，那么index=1与index=2,index=3就是多余的比较而画上了黄色。

2.当index=3的时候因为第一项就不匹配，于是出现时n=0，此时右移一位，同样后面也是这个道理。

3.当index=4的时候，因为第三项不匹配，于是出现n=2，而next[2]=0,按照上面法则就应该移动2位。这一行道理也很简单，因为T1=P1，T2=P2，但是P1!=P2，那么必然会有T2!=P1,所以index=5也是多余的。

 

事实上，以上图的目标字符串T：anndandnacanndana，匹配字符串P：anndana为例，当T（6）和P（6）出现不等的时候，此时取Next（6）=2，然后移动使得P（2）与T（6）比较。可是我们为什么会想到移动这么多位呢？因为对于P来说，前两项和第4,5两项相等都是an，此时算出来Next数组对应值为2，那么第2,3两项也就是nd断然不会与前两项或者第4,5两项相等，可以想象假如相等，那么next数组对应的值就不是2了，所移动的位数也会发生改变。因为next数组决定了字符串的特诊，而KMP算法巧妙的利用这条已经比较过的信息来规避掉多余的比较。细细品味，其他类型的字符串也很巧妙，但是本质还是一样的。

void getnext(int next[],string T)
{
    next[0]=-1;
    int i=0,j=-1;
    while(i<T.length()-1)
    {
        if( (j==-1)||(T[i]==T[j]) )
        {
            i++;
            j++;
            if(T[i]!=T[j]) next[i]=j;
            else next[i]=next[j];
        }
        else
            j=next[j];
    }
}
int KMP(int pos,string M,string N)
{
    int next[100];
    getnext(next,N);
    int i=pos-1,j=0;
    int mlen=M.length(),nlen=N.length();
    while( (i<mlen )&&(j<nlen ))
    {
        if( (j==-1)||(M[i]==N[j]) )
        {
            i++;j++;
        }
        else 
            j=next[j];
    }
    if(j>=nlen) return i-nlen+1;
    else return 0;
}