kmp算法详解

Posted 2021-09-15 捕获一只小肚皮

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了kmp算法详解相关的知识，希望对你有一定的参考价值。

文章目录

前言
例题引入
简单算法BF
经典算法KMP
kmp理解难点1
kmp理解难点2
kmp最难理解点3
kmp代码

前言

对于kmp的鼎鼎大名,不只是博主自己,想必还有更多小伙子们听说过,也相信都去了解过,博主亦是这样,但是真正去理解这个过程,确是异常的折磨人,在kmp算法里面捣鼓了整整3天,博主终于找到了用更好理解的话语进行解释了,便迫不及待的进行分享.

例题引入

假如有一个文本串T,内容为cadefgdefghp,有一个模式串P,其内容为defgh,请问P是否在T内?如果在,请返回P在T中的索引位置,如果不在,请返回-1.

简单算法BF

对于此题,我想大部分人都有一个简单思路,那就是T和P一一匹配,当匹配一个字符后,就挨个匹配后面;如果在中间部分不匹配,那么T讲回到最开始匹配字符的下一个字符处,P回到索引为0处.如下图:

而这种算法我们称为朴素算法(BF),代码博主会贴在下面:

int BF(char T[], char P[])
{
    int i = 0, j = 0;
    while (i < strlen(T) && j < strlen(P))
    {
        if (T[i] == P[j])  //如果相等,就继续从这往后匹配
        {
            i++, j++;
        }
        else
        {
            i = i - j + 1;     //如果不等,i就返回最开始匹配位置下一个位置(见上图)
            j = 0;             //p返回到索引为0重新开始
        }
    }
    if (j >= strlen(P))   //当匹配成功时,j一定移动到P字符串末尾,所以j必须有此条件
        return i - j;
    else 
        return -1;
}

经典算法KMP

为什么有KMP,他的目的就是解决我们重复匹配的问题,比如下图:

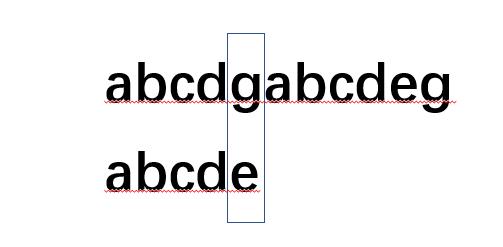
我们发现g和e不匹配了,按照BF算法,文本串(上方字符串)位置会回到b位置,模式串(下方)会重新回到索引为0处然后继续比对.

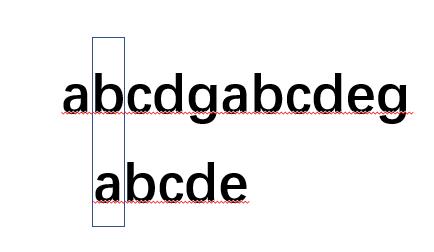
而如果我们按照人的思维会怎样继续对比呢?没错,我们并不会像BF那样笨,如果是人,会直接让文本串不动,直接让模式串开始重新匹配:

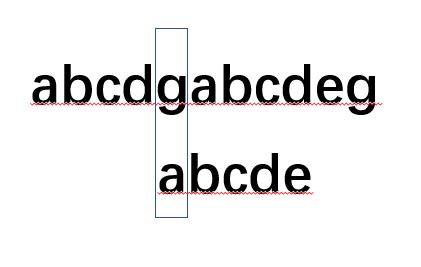
也就是文本串此时索引不动,而模式串索引回到了0,并从此处开始继续匹配.记住这句话!!!

我们再举一个例子,假设在文本串efabcabpabcabe中匹配abcabe,如下图:

我们先是一个一个的匹配,但是当匹配到p和e时,发现不匹配了,按照BF算法,文本串会回到索引为3位置,模式串会回到索引为0位置.

但是如果是人呢?会怎样做?我们会让模式串索引0位置和文本串索引5位置对齐,因为对齐后都有ab,所以模式串就从索引为2位置继续进行匹配.

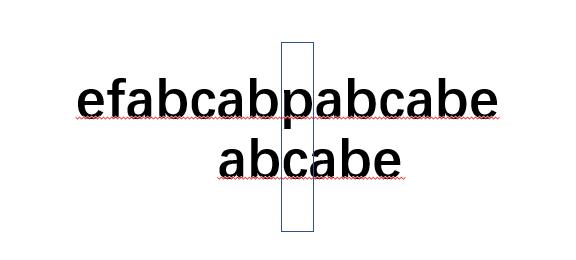
也就是文本串此时不动,而模式串索引回到2,并从此开始继续匹配.记住这句话!!!

我们最后再举一个例子:假设有文本串efabcdabcabcabe,模式串abcdabc,然后开始正常匹配

在这里,我们发生了失配,如果按照BF算法,我们会让文本串回到索引为3位置处,而模式串回到索引0处:

但是如果是人类呢? 会怎样做? 没错,我们会让模式串与文本串的索引6位置处对齐,而文本串不动.然后发现对齐以后,文本串和模式串都有abc,所以我们不管abc,而是让模式串从索引为3处开始和文本串对比:

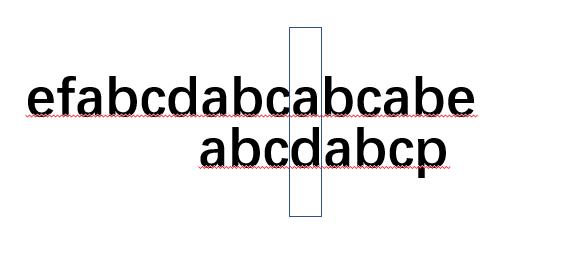
也就是文本串此时不动,而模式串索引回到3,并从此开始继续匹配.记住这句话!!!

大家分别纵观上面三个例子,我们都做了什么相同操作?

当失配时:
- 文本串位置不动
- 模式串的索引直接从某个位置开始继续和文本串适配位置进行匹配

我们再来看看规律,

第一个例子: 文本串此时不动,而模式串索引回到0,并从此开始继续匹配.

原因:模式串失配位置前面有0个重复的元素

第二个例子:文本串此时不动,而模式串索引回到2,并从此开始继续匹配.

原因: 模式串失配位置前面有2个重复的元素,即ab

第三个例子:文本串此时不动,而模式串索引回到3,并从此开始继续匹配.

原因: 模式串失配位置前面有3个重复的元素,即abc

也就是说!!!,当在中途匹配过程中发生失败,我可以不再让文本串回走很长一段举例,而是让模式串进行继续匹配,至于模式串下一步应该会到哪个位置,取决于匹配失败字符前的相同前后缀字符(后面会介绍前后缀)长度

我们再试试一个例子,看看是这个规律吗?比如文本串efacadmp,模式串acabef

此时失配了,模式串失配字符b前面有1个重复的元素a,所以模式串直接从索引为1开始进行继续匹配,看看是否对:

完全没问题,因为在模式索引0前有一个字符a,而文本串对应位置也有一个字符a,所以模式串直接从索引为1开始匹配

也就是说一旦发生失配,人类执行时,会按照如下步骤:

不动文本串
模式串位置直接回到索引为k处(k是失配位置前面所有字符串中最大重复元素数量)

而这些步骤用代码写出来就是kmp

即kmp算法不像BF算法那样,避免了文本串的索引返回,而是直接定位模式串下一个匹配位置.

kmp理解难点1

我们已经清楚了kmp的算法步骤,而难点1就在于求k

而k就是字符串的最大相同前后缀长度

**前后缀概念: **

前缀: 字符串中除了最后一个字符外的所有顺序集合
- 比如有字符串abcdef,那么他的前缀有a,ab,abc,abcd,abcde
后缀:字符串中除了第一个字符外的所有顺序集合
- 比如有字符串abcdef,那么他的后缀有f,ef,def,cdef,bcdef
最大相同前后缀: 前缀集合和后缀集合的交集中最大长度者
- 比如有字符串ababab,他的前后缀交集有ab,abab,所以最长相同前后缀就是abab

kmp理解难点2

我们知道,当模式串与主串不匹配时,而主串不动,模式串的索引跳到k处,k值是b当前不匹配字符前的所有字符中最大相同前后缀长度

所以我们为了方便处理,便用一个数组进行储存一段字符串的最大前后缀最长度

假设有字符串ababaaaba,则:

字符串	a	b	a	b	a	a	a	b	a
索引	0	1	2	3	4	5	6	7	8
k值	0	0	1	2	3	1	1	2	1

解释:

在索引为3下,k值是2,代表着[0,3]中的字符串中相同前后缀的最大长度为2
在索引为6下,k值是1,代表着[0,6]中的字符串中相同前后缀的最大长度为1
在索引为0下,k值0,代表着[0,0]中的字符串,即一个字符是没有前后缀的,最大长度为0

我们给储存k值的数组起名叫做next.这也就是我们kmp算法中的精华所在

kmp最难理解点3

博主在学习kmp算法中时候,发现很多文章与视频都是只给了手动算next数组方法,对于代码部分便是一笔跳过,而这才是KMP中最最最难理解的一部分代码,下面博主用自己的理解给大家分享下自己的拙见

我们还是像介绍kmp算法一样,我们还是先用自己的第一思路来处理,然后写代码,最后进阶精华kmp数组求法:

我们的第一思路是什么? 没错,那就是前缀和后缀一对一对的比较,比如有下面一段字符串str:

abbabba

我们用变量i进行指示比的是第几对,从1开始.

我们用变量count进行计数,当出现一对相同前后缀,则count = i,最后count值就是最大长度

当i = 1时候,第一对前缀是"a",后缀是"a",后缀的位置是strlen(str)-1,前后缀相同,count等于1
当i = 2时候,第一对前缀是"ab",后缀是"ba",后缀的位置是strlen(str)-2,前后缀不同,count不管
…
当i = 4时候,第一对前缀是"abba",后缀是"abba",后缀的位置是strlen(str)-4,前后缀相同,count等于4
…

所以大概代码如下:

int count = 0;
for(int i = 1;i < strlen(str);i++)               //i不能等于strlen(str),因为前后缀分别不包含尾字符和首字符
{
    if(strncmp(str,str+strlen(str)-i,i) == 0)    //如果第几对前后缀相同,则count等于几
    {                                            //str+strlen(str)-i 是指针加减整数的意义
        count = i;
    }
}

而我们是需要求一个数组,所以我们就把字符串拆成更多个小字符串,然后又分别求每个小字符串的最大前后缀长度,思路和上面一样

void next(char str[],int next[])
{
    int i = 1,j = 1,count = 0;
    //i代表第几对,j代表索引[0,j]的字符串,count代表最大长度   
    
    next[0] = 0; //首字符一定为0,因为之后一个字符,没有前后缀
    
    for(j = 1;j<strlen(str);j++)
    {
        count = 0;
        for(int i = 1;i < strlen(str);i++)               //i不能等于strlen(str),因为前后缀分别不包含尾字符和首字符
        {
            if(strncmp(str,str+strlen(str)-i,i) == 0)    //如果第几对前后缀相同,则count等于几
            {                                            //str+strlen(str)-i 是指针加减整数的意义
                count = i;
            }
        }
        next[j] = count;
    }
}

我们已经成功的用自己的方法求出来了next数组,但是大家有没有发现这样求解有一个很大的缺陷?

那就是我们每次在求解[0,j]中的字符串最大相同前后缀时,我们都是从第一对的一个字符,到第j对的j个字符进行对比.
而在求解[0,j+1]中的字符串最大相同前后缀时,我们又要从第一对的第一个字符,到第j+1对的j+1个字符进行对比.

在比较的过程中我们比较了很多不相同前后缀的字符串,那么我们想一想,可不可以换一种思路,不再像上面那样每次都要从一个字符开始进行匹配,避免多次匹配不相同前后缀字符串? 答案是完全可以!!!

下面,请大家一定记住这句话,不要觉得这些话很简单,后面正是这些话才能明白某些代码:

相同前后缀 == 相同前缀 == 相同后缀 !!!— --- — --- — --- — --- — --- — --- — --- — --- — --- — --- — --- ---- — --- — ---标号①

如果一段字符串存在相同前后缀,那么相同前缀一定可以在后缀(注意,没有相同两字)中找到,并且相同前缀一定是最长后缀末尾,相同前缀的长度一定小于等于最长后缀长度— --- — --- — --- — --- — --- — --- — --- — --- — --- — --- — --- —标号②

举个例子:

有一段字符串ababa.

相同前后缀有a与aba,而后缀有a,ba,aba,baba,这就是这句话— --- —相同前缀一定可以在后缀中找到的意思
该段字符串最长后缀为baba,相同前缀为a,是最长后缀的末尾,相同前缀为aba,是最长后缀的末尾.
所以说— --- — 相同前缀一定是最长后缀末尾

相同前缀的长度分别是1和3都小于最长后缀的长度4

既然我们目的是为了减少不必要的不同前后缀字符串比对,那么我们的方法是什么呢?

答曰: 给最长相同前缀新增一个字符,然后判断是否在最长后缀中.(请看标号①语句)

如果不在,我们就判断原最长相同前缀是否在最长后缀中…
如果在,说明此时的字符串中最长相同前后缀长度是原最长相同前后缀长度加1(步骤重复上面)

我们现在要开始清楚一些概念了:

我们用j表示一段字符串([0,j]的字符串)最长后缀的尾巴的索引,j的初始值设为1
用k表示字符串中最长相同前缀的长度(这句话本身还表达了另一个意思,是最长相同前缀尾巴后一个索引,这个很重要),k初始为0
- 比如有字符串ababa,假设此时k等于3,说明此时最长相同前后值长度是3,而索引为3字符却是最长相同前缀尾末,
next数组存储的是最长相同前后缀字符长度,则next[j]表示索引在[0,j]的字符串中最长相同前后缀的长度

所以他们一定有下图关系:

现在大家再看看上面我们说的新的比较方法的步骤,然后下面的代码结合上面这张图分析

(下面这些话大家一定要静下心来想,博主会贴图再详细解释)

如果不存在,怎么判断?

答曰:

while(k>0 && p[k] != p[j])  //k为什么大于0,后面会解释
{
    k = next[k-1];         //说明给原最长相同前缀加一个字符后,判断出不等,即[0,k]的字符串不在后缀中
}

其实k = next[k-1]大家可能还是不理解,但是大家想想我们的目的,避免比较不相同前后缀,而next数组装的就只有相同前后缀长度.
既然[0,k]字符串的最长前缀不在后缀中,我们就需要比较[0,k-1]中的最长前缀是否在后缀.
    而next[k-1]的意义不就是[0,k-1]中最长相同前后缀字符串长度吗?

给最长相同前缀新增一个字符,如何判断在最长后缀中?

**答曰: **

if(p[k] == p[j])    //因为p[0,k-1]等于p[j-k,j-1],而p[0,k-1]就是目前为止最长相同前缀,所以只需要判断p[k]和p[j]了
{
    next[j] = k+1; //如果相等,[0,j]中的最长相同前后缀长度等于原最长前后缀长度加一.
    k++;           //更新现在的最长相同前后缀长度
}
else               //else就是处理当k等于0,且p[k]不等于p[j]时候,说明next[j]应该为0
{
    next[j] = 0;
}

所以最后求next数组的代码就是

void get_next(char p[100],int next[100]) 
{

    next[0] = 0;
    int j = 1;
    int k = 0;
    //如果有效前缀增加一个值和新增后缀不等,
    for(j = 1; j < strlen(p); j++)
    {
        while (k>0 && p[k] != p[j])
        {
            k = next[k - 1];   
        }
        if (p[k] == p[j])
        {
            next[j] = ++k;
        }
        else   //这一步是索引为1时候,k等于0,且不等的条件
        {
            next[j] = 0;
        }
    }
}

kmp代码

int kmp(char s[100],char p[100])
{
    int i = 0, j = 0;
    int next[100];
    get_next(p,next);
    while (i < strlen(s) && j < strlen(p))
    {
        if (s[i] == p[j])
        {
            i++, j++;
        }
        else if (j > 0)
        {
            j = next[j - 1];
        }
        else
        {
            i++;
        }
    }

    if (j >= strlen(p)) return i - j;
    else
        return -1;
}

以上是关于kmp算法详解的主要内容，如果未能解决你的问题，请参考以下文章

KMP算法详解以及Java代码实现

数据结构KMP算法配图详解（超详细）

疫情封校在宿舍学习KMP算法详解（next数组详解）附例

kmp 算法详解

kmp算法详解

KMP算法详解