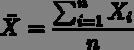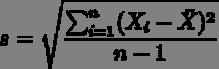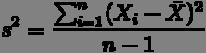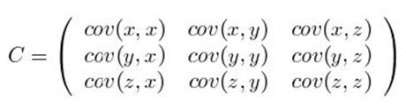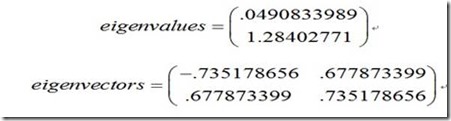主成分分析（principal components analysis, PCA）

Posted 2020-08-04 ParamousGIS

 

原理

 

计算方法

 

主要性质

 

有关统计量

 

主成分个数的选取

 

 

------------------------------------------------------------------------------------------------------------------------

http://my.oschina.net/gujianhan/blog/225241

-------------------------------------------------------------------------------------------------------------------------

 

一、简介

       PCA（Principal Components Analysis）即主成分分析，是图像处理中经常用到的降维方法，大家知道，我们在处理有关数字图像处理方面的问题时，比如经常用的图像的查询问题，在一个几万或者几百万甚至更大的数据库中查询一幅相近的图像。这时，我们通常的方法是对图像库中的图片提取响应的特征，如颜色，纹理，sift，surf，vlad等等特征，然后将其保存，建立响应的数据索引，然后对要查询的图像提取相应的特征，与数据库中的图像特征对比，找出与之最近的图片。这里，如果我们为了提高查询的准确率，通常会提取一些较为复杂的特征，如sift，surf等，一幅图像有很多个这种特征点，每个特征点又有一个相应的描述该特征点的128维的向量，设想如果一幅图像有300个这种特征点，那么该幅图像就有300*vector（128维）个，如果我们数据库中有一百万张图片，这个存储量是相当大的，建立索引也很耗时，如果我们对每个向量进行PCA处理，将其降维为64维，是不是很节约存储空间啊？对于学习图像处理的人来说，都知道PCA是降维的，但是，很多人不知道具体的原理，为此，我写这篇文章，来详细阐述一下PCA及其具体计算过程：

二、PCA详解

1、原始数据：

为了方便，我们假定数据是二维的，借助网络上的一组数据，如下：

x=[2.5, 0.5, 2.2, 1.9, 3.1, 2.3, 2, 1, 1.5, 1.1]T
y=[2.4, 0.7, 2.9, 2.2, 3.0, 2.7, 1.6, 1.1, 1.6, 0.9]T

2、计算协方差矩阵

什么是协方差矩阵？相信看这篇文章的人都学过数理统计，一些基本的常识都知道，但是，也许你很长时间不看了，都忘差不多了，为了方便大家更好的理解，这里先简单的回顾一下数理统计的相关知识，当然如果你知道协方差矩阵的求法你可以跳过这里。

（1）协方差矩阵：

首先我们给你一个含有n个样本的集合，依次给出数理统计中的一些相关概念：

均值：
标准差：
方差：

既然我们都有这么多描述数据之间关系的统计量，为什么我们还要用协方差呢？我们应该注意到，标准差和方差一般是用来描述一维数据的，但现实生活我们常常遇到含有多维数据的数据集，最简单的大家上学时免不了要统计多个学科的考试成绩。面对这样的数据集，我们当然可以按照每一维独立的计算其方差，但是通常我们还想了解这几科成绩之间的关系，这时，我们就要用协方差，协方差就是一种用来度量两个随机变量关系的统计量，其定义为：

从协方差的定义上我们也可以看出一些显而易见的性质，如：

(X的方差)

需要注意的是，协方差也只能处理二维问题，那维数多了自然就需要计算多个协方差，比如n维的数据集就需要计算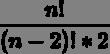个协方差，那自然而然的我们会想到使用矩阵来组织这些数据。给出协方差矩阵的定义：

这个定义还是很容易理解的，我们可以举一个简单的三维的例子，假设数据集有三个维度，则协方差矩阵为

可见，协方差矩阵是一个对称的矩阵，而且对角线是各个维度上的方差。

（2）协方差矩阵的求法：

协方差矩阵计算的是不同维度之间的协方差，而不是不同样本之间的。下面我们将在matlab中用一个例子进行详细说明：

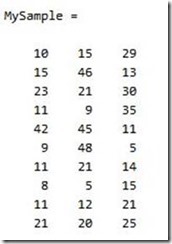
首先，随机产生一个10*3维的整数矩阵作为样本集，10为样本的个数，3为样本的维数。
MySample = fix(rand(10,3)*50)

根据公式，计算协方差需要计算均值，那是按行计算均值还是按列呢，我一开始就老是困扰这个问题。前面我们也特别强调了，协方差矩阵是计算不同维度间的协方差，要时刻牢记这一点。样本矩阵的每行是一个样本，每列为一个维度，所以我们要按列计算均值。为了描述方便，我们先将三个维度的数据分别赋值：

dim1 = MySample(:,1);
dim2 = MySample(:,2);
dim3 = MySample(:,3);

计算dim1与dim2，dim1与dim3，dim2与dim3的协方差：

sum( (dim1-mean(dim1)) .* (dim2-mean(dim2)) ) / ( size(MySample,1)-1 ) % 得到  74.5333
sum( (dim1-mean(dim1)) .* (dim3-mean(dim3)) ) / ( size(MySample,1)-1 ) % 得到  -10.0889
sum( (dim2-mean(dim2)) .* (dim3-mean(dim3)) ) / ( size(MySample,1)-1 ) % 得到  -10***000

搞清楚了这个后面就容易多了，协方差矩阵的对角线就是各个维度上的方差，下面我们依次计算：

std(dim1)^2 % 得到   108.3222
std(dim2)^2 % 得到   260.6222
std(dim3)^2 % 得到  94.1778

这样，我们就得到了计算协方差矩阵所需要的所有数据，调用Matlab自带的cov函数进行验证：

cov(MySample)

可以看到跟我们计算的结果是一样的，说明我们的计算是正确的。但是通常我们不用这种方法，而是用下面简化的方法进行计算：

先让样本矩阵中心化，即每一维度减去该维度的均值，然后直接用新的到的样本矩阵乘上它的转置，然后除以(N-1)即可。其实这种方法也是由前面的公式通道而来，只不过理解起来不是很直观而已。大家可以自己写个小的矩阵看一下就明白了。其Matlab代码实现如下：

X = MySample – repmat(mean(MySample),10,1);    % 中心化样本矩阵
C = (X’*X)./(size(X,1)-1)

（为方便对matlab不太明白的人，小小说明一下各个函数，同样，对matlab有一定基础的人直接跳过：

B = repmat(A,m,n ) %%将矩阵 A 复制 m×n 块，即把 A 作为 B 的元素，B 由 m×n 个 A 平铺而成。B 的维数是 [size(A,1)*m, (size(A,2)*n] 

B = mean(A)的说明：

如果你有这样一个矩阵：A = [1 2 3; 3 3 6; 4 6 8; 4 7 7];
用mean(A)（默认dim=1）就会求每一列的均值
ans =
    3.0000    4.5000    6.0000
用mean(A,2)就会求每一行的均值
ans =
    2.0000
    4.0000
    6.0000

   6.0000

size(A,n)%% 如果在size函数的输入参数中再添加一项n，并用1或2为n赋值，则 size将返回矩阵的行数或列数。其中r=size(A,1)该语句返回的是矩阵A的行数， c=size(A,2) 该语句返回的是矩阵A的列数）

上面我们简单说了一下协方差矩阵及其求法，言归正传，我们用上面简化求法，求出样本的协方差矩阵为：

3、计算协方差矩阵的特征向量和特征值

因为协方差矩阵为方阵，我们可以计算它的特征向量和特征值，如下：

[eigenvectors,eigenvalues] = eig(cov)

我们可以看到这些矢量都是单位矢量，也就是它们的长度为1，这对PCA来说是很重要的。

4、选择成分组成模式矢量

求出协方差矩阵的特征值及特征向量之后，按照特征值由大到小进行排列，这将给出成分的重要性级别。现在，如果你喜欢，可以忽略那些重要性很小的成分，当然这会丢失一些信息，但是如果对应的特征值很小，你不会丢失很多信息。如果你已经忽略了一些成分，那么最后的数据集将有更少的维数，精确地说，如果你的原始数据是n维的，你选择了前p个主要成分，那么你现在的数据将仅有p维。现在我们要做的是组成一个模式矢量，这只是几个矢量组成的矩阵的一个有意思的名字而已，它由你保持的所有特征矢量构成，每一个特征矢量是这个矩阵的一列。

对于我们的数据集，因为有两个特征矢量，因此我们有两个选择。我们可以用两个特征矢量组成模式矢量：

我们也可以忽略其中较小特征值的一个特征矢量，从而得到如下模式矢量：

5、得到降维后的数据

其中rowFeatureVector是由模式矢量作为列组成的矩阵的转置，因此它的行就是原来的模式矢量，而且对应最大特征值的特征矢量在该矩阵的最上一行。rowdataAdjust是每一维数据减去均值后，所组成矩阵的转置，即数据项目在每一列中，每一行是一维，对我们的样本来说即是，第一行为x维上数据，第二行为y维上的数据。FinalData是最后得到的数据，数据项目在它的列中，维数沿着行。

这将给我们什么结果呢？这将仅仅给出我们选择的数据。我们的原始数据有两个轴（x和y），所以我们的原始数据按这两个轴分布。我们可以按任何两个我们喜欢的轴表示我们的数据。如果这些轴是正交的，这种表达将是最有效的，这就是特征矢量总是正交的重要性。我们已经将我们的数据从原来的xy轴表达变换为现在的单个特征矢量表达。

（说明：如果要恢复原始数据，只需逆过程计算即可，即：

）