用PCA降维 （Principal Component Analysis，主成分分析)

Posted 2020-10-05

参考资料：Mastering Machine Learning With scikit-learn

　　降维致力于解决三类问题。第一，降维可以缓解维度灾难问题。第二，降维可以在压缩数据的同时让信息损失最 小化。第三，理解几百个维度的数据结构很困难，两三个维度的数据通过可视化更容易理解

• PCA简介

　　主成分分析也称为卡尔胡宁-勒夫变换（Karhunen-Loeve Transform），是一种用于探索高维数据结 构的技术。PCA通常用于高维数据集的探索与可视化。还可以用于数据压缩，数据预处理等。PCA可 以把可能具有相关性的高维变量合成线性无关的低维变量，称为主成分（ principal components）。 新的低维数据集会经可能的保留原始数据的变量。

• PCA计算步骤
• 方差，协方差和协方差矩阵

　　方差（Variance）是度量一组数据分散的程度。方差是各个样本与样本均值的差的平方和的均值：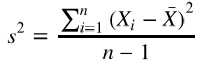

　　协方差（Covariance）是度量两个变量的变动的同步程度，也就是度量两个变量线性相关性程度。如果两个变量的协方差为0，则统计学上认为二者线性无关。注意两个无关的变量并非完全独立，只是没有线性相关性而已。计算公式如下：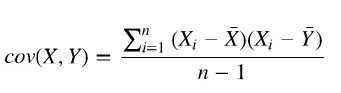

　　如果协方差不为0，如果大于0表示正相关，小于0表示负相关。当协方差大于0时，一个变量增大另一个变量也会增大。当协方差小于0时，一个变量增大另一个变量会减小。协方差矩阵 （Covariance matrix）由数据集中两两变量的协方差组成。矩阵的第 个元素是数据集中第 和第个元素的协方差。例如，三维数据的协方差矩阵如下所示：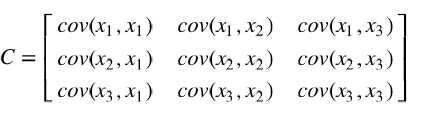

• 特征向量和特征值

　　向量是具有大小（magnitude）和方向（direction）的几何概念。特征向量（eigenvector）是一个矩 阵的满足如下公式的非零向量：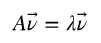

• 用PCA降维

　　scikit-learn的实现方法是用奇异值分解计算特征值和特征向量，SVD（ singular value decomposition method；奇异值分解法）计 算公式如下：

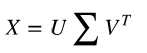
　　列向量 U称为数据矩阵的左奇异值向量，v称为数据矩阵的右奇异值向量，∑的对角线元素是它的奇异值。矩阵的奇异值向量和奇异值在一些信号处理和统计学中是十分有用，这里只对它们与数据矩阵特征向量和特征值相关的内容感兴趣。具体来说，左奇异值向量就是协方差矩阵的特征向量，∑的对角线元素是协方差矩阵的特征值的平方根。

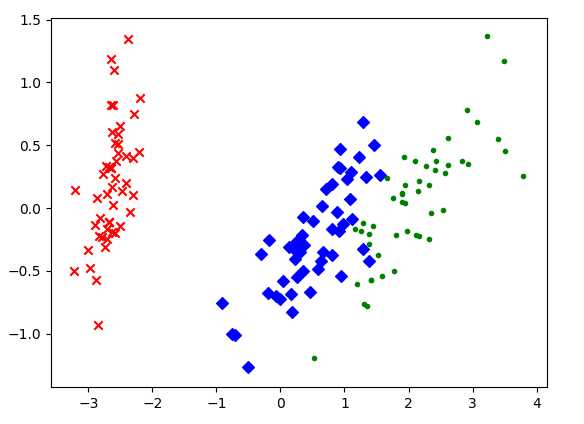
• 用PCA实现高维数据可视化

import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.datasets import load_iris

data = load_iris()
y = data.target
X = data.data
pca = PCA(n_components=2)
reduced_X = pca.fit_transform(X)
print(X)
print(reduced_X)

red_x, red_y = [], []
blue_x, blue_y = [], []
green_x, green_y = [], []
for i in range(len(reduced_X)):
    if y[i] == 0:
        red_x.append(reduced_X[i][0])
        red_y.append(reduced_X[i][1])
    elif y[i] == 1:
        blue_x.append(reduced_X[i][0])
        blue_y.append(reduced_X[i][1])
    else:
        green_x.append(reduced_X[i][0])
        green_y.append(reduced_X[i][1])
plt.scatter(red_x, red_y, c=‘r‘, marker=‘x‘)
plt.scatter(blue_x, blue_y, c=‘b‘, marker=‘D‘)
plt.scatter(green_x, green_y, c=‘g‘, marker=‘.‘)
plt.show()