A tutorial on Principal Components Analysis | 主成分分析(PCA)教程
Posted houchaoqun
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了A tutorial on Principal Components Analysis | 主成分分析(PCA)教程相关的知识,希望对你有一定的参考价值。
A tutorial on Principal Components Analysis
原著:Lindsay I Smith, A tutorial on Principal Components Analysis, February 26, 2002.
翻译:houchaoqun.
时间:2017/01/18.
出处:http://blog.csdn.net/houchaoqun_xmu | http://blog.csdn.net/Houchaoqun_XMU/article/details/54601984
说明:本文在翻译原文的过程中,在保证不改变原文意思的前提下,对一些知识点进行了扩充并附上参考网址。本人刚开始尝试翻译文献,经验不足,有些理解可能不到位,有些翻译可能不够准确。若读者们有发现有误之处,还望海涵并加以指正,本人会及时加以指正。
- 本文中涉及到公式的编辑,使用的是“在线LaTeX公式编辑器”,将编辑完成后的公式(图片的形式)复制到博文中即可。
- 原文可能缺少一些图,本人通过Matlab作图并补充。
- 本人在原文的基础上,额外提供了一些参考网址,有兴趣的读者们可以详细阅读。
- 为了更读者更深刻的理解PCA,本人还另外提供了案例,并用Matlab实现,仅供读者们参考。
- 为了更好的将理论运用到实际,本人打算在介绍完这篇PCA教程后,整理一篇基于PCA进行人脸识别的具体案例,由于水平有限,需要改正和完善的地方希望读者们提供宝贵的意见。
--------------------------------
主成分分析(PCA)教程
第1章:简介(Introduction)
本教程的目的是为了让读者理解主成分分析(PCA)。PCA是一项很有用的统计学技术,已经应用在人脸识别(Face Recognition)和图像压缩(Image Compression)等领域,并且作为一项通用技术在高维数据中发现数据模型(降维技术)。
开始介绍PCA之前,本教程首先介绍一些学习PCA相关的数学概念。包括,标准差,协方差,特征向量及其对应的特征值。这部分背景知识旨在使得PCA相关的章节更加简洁明了,如果读者对这部分的概念很熟悉,可以选择跳过这部分内容。
本教程的一些相关案例旨在说明这些数学概念,让读者对这部分内容理解得更加深刻。如果读者想要更进一步的学习,“初等线性代数 第五版(Elementary Linear Algebra 5e)”这本数学工具书是一个很好的关于这些数学背景的资源。这本书的作者是Howard Anton,由John Wiley和Sons股份有限公司出版(国际标准图书编号[ISBN] 0-471-85223-6)。
第2章:数学背景(Background Mathematics)
本章将给出一些对于理解PCA原理(涉及相关的推导过程)所需的基础数学技能。这部分知识都是相互独立的,并且都有相关的例子。理解为什么可能使用到这个技术以及在数据方面,某个操作的结果告诉了我们什么,比记住准确的数学技术更重要。虽然并不是这些技术都运用到PCA,但是最重要的技术(运用到PCA的技术)正是基于那些没有明确需要的技术(没有明确运用到PCA),所以对于初学者,还是有必要好好理解一下各个知识点。
本章包含两大部分,第一部分介绍了关于统计学的知识,侧重于介绍数据(分布测量)是如何分布的(标准差,方差,协方差以及协方差矩阵)。第二部分介绍了矩阵代数,侧重于特征向量和特征值,矩阵的一些重要性质是理解PCA的基础。
2.1 统计学(Statistics)
关于统计学的整个主题是围绕着你有一个大的数据集,并且你想要分析这个数据集中点跟点之间的关系。本章将侧重介绍一些读者能够亲自操作(手算验证)的测量指标(标准差,方差,协方差以及协方差矩阵),并且对于数据本身,这些测量指标告诉了我们什么(即,测量值反映数据的关系)。
2.1.1 标准差(Standard Deviation)
为了理解标准差,我们需要一个数据集,统计学家通常使用来自总体(population)中的一个样本(sample)。此处使用选举投票(election polls)为例,“总体”是这个国家的所有人,而统计学家测量(measure)的样本是这个总体的一个子集。统计学的伟大之处在于仅仅通过测量(可以通过电话调查或者类似的方法)总体中的一个样本,就能够算出与总体最相似的测量结果(即,通过测量样本进而解决总体)。在统计学这个章节,作者假设本文使用的数据集是来自更大总体的样本(总体的数据集比样本的数据集更大)。(本章)下文有一个关于样本和总体更详细信息的参考网址。
例如,对于数据集X:
我们简单的使用符号X表示整个数据集。如果想表示数据集中的某个元素,可以使用下标表示指定的元素(值),如 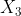 表示数据集X的第三个元素,对应的值是4;
表示数据集X的第三个元素,对应的值是4;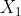 指的是这个序列中的第一个元素,值为1;但是这里并没有像我们在一些教科书上提到的
指的是这个序列中的第一个元素,值为1;但是这里并没有像我们在一些教科书上提到的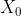 (因为此处的下标从1开始)。此外,符号n表示数据集X的元素个数。
(因为此处的下标从1开始)。此外,符号n表示数据集X的元素个数。
我们可以对一组数据集进行很多种计算。例如,我们可以计算这个样本(数据集)的平均值(mean)。作者假设读者们理解样本X的均值的含义,此处仅给出计算公式,如下:
注:符号 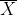 表示数据集X的均值。上述公式表示,“累加数据集X中的所有元素的值,然后除以元素总数n”。
表示数据集X的均值。上述公式表示,“累加数据集X中的所有元素的值,然后除以元素总数n”。
不幸的是,均值仅仅告诉我们数据集的中间点。例如,以下两组数据集具有相关的均值(mean = 10),但是这是两组完全不同的数据。
因此,这两组数据集有什么不同呢?数据的分布不同。数据集的标准差反映了数据是如何分布的(个体间的离散程度)。
我们要怎样计算标准差(Standard Deviation)呢?标准差(SD)的英文定义是,“The average distance from the mean of the data set to a point(数据集中每个点到均值的平均距离)”。标准差的计算方式是,首先计算每个点到样本均值的距离的平方,然后进行累加,最后将累加的结果除以 n-1 再开根号,如下公式所示:
其中,通常使用s表示一个样本的标准差。读者可能会问,“为什么是除以 (n-1) ,而不是 n?”。答案有些复杂,但总的来说,如果你的数据集是样本数据集,也就是说如果你选择的是一个真实世界中的子集(例如,对样本数为500个人的选举投票案例进行测量),你就需要使用 (n-1) 。因为事实证明,对于样本,使用(n-1)得到的答案更接近于标准差的结果(如果你尝试使用Matlab提供的cov函数,也是除以n-1)。如果你处理的数据集是总体,那你应该使用n。(其他解释参考[ 点击进入链接 ]:如是总体,标准差公式根号内除以n,如是样本,标准差公式根号内除以(n-1);这样能使我们以较小的样本集更好的逼近总体的标准差,即统计上所谓的“无偏估计”)。不管怎样,如果你计算的不是样本的标准差,而且总体的标准差,那么公式根号内应该除以n,而不是(n-1)。对于这部分内容,有意愿更进一步了解的读者可以参考网址:http://mathcentral.uregina.ca/RR/database/RR.09.95/weston2.html。这个网址用相似的方式介绍了标准差,还提供了一个实验案例,解释了标准差公式根号内的两种分母(即,n和n-1)的区别,并对“样本”和“总体”的区别进行了讨论。
如下表2.1所示的两组数据,分别计算了它们的标准差。

正如预期的,表2.1的第一部分的标准差(8.3266)更大是因为这组样本数据相对于均值的分布更离散。正如另一个例子所示,样本数据为[ 10 10 10 10 ],均值同样为10,但是它的标准差为0。因为所有元素的值都一样,不存在偏离均值的元素。
2.1.2 方差(Variance)
方差是另一种测量数据集离散程度的方式。实际上,方差和标准差几乎是相同的。公式如下:
读者们可以发现方差仅仅是对标准差等式左右两边进行平方(方差的公式中没有对其开根号)。对于样本中的方差 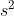 是常用的符号。这两个衡量值(方差和标准差)都是衡量数据的离散程度。标准差是最常用的衡量值,但方差同样适用。本文在介绍了标准差之外,还介绍方差的原因是为下一个章节的协方差提供基础(铺垫,抛砖引玉)。
是常用的符号。这两个衡量值(方差和标准差)都是衡量数据的离散程度。标准差是最常用的衡量值,但方差同样适用。本文在介绍了标准差之外,还介绍方差的原因是为下一个章节的协方差提供基础(铺垫,抛砖引玉)。
练习:如下三组数据集所示,分别求出均值,标准差和方差。
- [ 12 23 34 44 59 70 98 ]
- [ 12 15 25 27 32 88 89 ]
- [ 15 35 78 82 90 96 97 ]
2.1.3 协方差(Covariance)
上述我们关注的两种(标准差和方差)测量指标的对象仅仅是一维数据集(局限性),比如房间里所有人的身高或者教师批改试卷等。然而,许多数据集都不只是一维,而且对于这些数据集,统计分析的目标通常是寻找这些维度之间是否存在任何关系。例如,我们将班级上所有学生的身高以及学生考试的分数作为数据集,然后使用统计分析方法去判断学生的身高是否对他们的分数有任何影响。
标准差和方差仅仅处理一维数据,因此你只能分别对数据集中的每一维计算出标准差(每一维对应一个标准差)。然而,找到一种与上述相似,并且能够度量各个维度偏离其均值程度的测量指标是非常有用的。
【协方差】就是这样的一种测量指标。协方差通常用来测量2维的数据集。如果你计算的协方差中的2个维度都是同一个变量,此时得到的就是方差。(协方差正常处理的是二维数据,维数大于2的时候,就用协方差矩阵表示)因此,如果有一组三维数据集(x, y, z),那么我们需要分别计算x维度和y维度,x维度和z维度,y维度和z维度的协方差。计算x维度和x维度,y维度和y维度,z维度和z维度的协方差就相当于分别计算x,y,z维度的方差(这就是两个维度都是同一个变量的情况)。
协方差的公式和方差的公式很相似,方差的公式(度量各个维度偏离其均值的程度)如下所示:
其中,作者仅仅是拓展了平方项变成两个部分(如,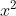 表示成
表示成 *
*  )。因此,协方差的公式如下:
)。因此,协方差的公式如下:
上述两个公式(方差和标准差)除了分子中的第二个括号内将X用Y代替以为,其他都一样。用英文定义就是,“For each data item, multiply the different between the x value and the mean of x, by the difference between the y value and the mean of y. Add all these up, and divide by (n -1)”(对于X和Y的每个数据项,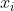 与
与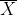 (变量X的均值)的差乘以
(变量X的均值)的差乘以 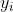 与
与 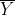 (变量Y的均值)的差,然后将它们累加起来后除以 (n-1) )。
(变量Y的均值)的差,然后将它们累加起来后除以 (n-1) )。
那么,协方差是如何运作的呢?让我们使用一些实例数据。想象我们走进世界中,收集到一些二维数据。我们统计一群学生用在学习 COSC241 这个课程的时间(小时)以及他们获得的分数。现在我们有了二维的数据,第一维是H维,表示学生学习的时间(以小时为单位),第二维是M维,表示学生获得的分数。如下图所示,包含了我们刚刚想象的数据以及H和M之间的协方差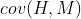 的计算结果。
的计算结果。

图示:学生学习的时间H,获得的分数M

那么,这些数据告诉我们什么?协方差的符号(正好或者负号)比数值更加重要。如果协方差的值是正数,表明这两维(H和M)是正相关,也就是说,随着学生学习的时间(H)的增加,学生获得的分数(M)也增加。如果值是负数,一个维度增加则另一个维度减小(数据呈负相关)。对于这个例子,如果协方差最终得到的结果是负值,也就是负相关,意味着随着学生学习时间的增加,学生获得的分数则减少。最后还有一种情况是,当协方差的值为0,意味着这两维(如,变量H和M)是相互独立的(不相关)。
实验结果(上述数据)可以很直观的通过对原始数据作图,如下图所示,学生所得的分数M随着学生学习的时间H的增加而增加。然而,数据的可视化(作图)也仅仅局限于2维和3维的数据。因为对于任意2维的数据都可以计算协方差的值,因此这项技术(协方差)经常用于发现高维数据之间的关系(这些高维数据是很难进行可视化的)。

读者们或许会问,“ 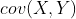 等于
等于  吗?”。通过协方差公式告诉我们,答案是“
吗?”。通过协方差公式告诉我们,答案是“ 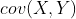 等于
等于  ”,(展开协方差公式)这两者唯一的区别就是式子
”,(展开协方差公式)这两者唯一的区别就是式子 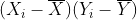 用式子
用式子 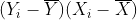 替代。根据“乘法交换律”可知,两个因数相乘,交换因数的位置,积不变,也就是说
替代。根据“乘法交换律”可知,两个因数相乘,交换因数的位置,积不变,也就是说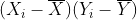 和
和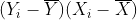 得到相同的结果。
得到相同的结果。
2.1.4 协方差矩阵(The Covariance Matrix)
回顾协方差的相关知识,它通常测量的是二维数据。假如我们有一组大于2维的数据,那么将有多个协方差可以计算(有多种组合形式的协方差)。例如,对于一个三维的数据(x, y, z),我们能够计算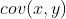 ,
, 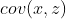 和
和 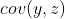 。实际上,对于一组n维数据,我们可以计算
。实际上,对于一组n维数据,我们可以计算 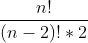 种不同组合的协方差。一种有用的方式是,“计算不同维度之间所有可能情况的协方差值,然后将它们放入一个矩阵”,构成协方差矩阵。(本教程假设读者们对矩阵很熟悉并且知道如何去定义矩阵)。因此,一组n维数组的协方差矩阵的定义如下:
种不同组合的协方差。一种有用的方式是,“计算不同维度之间所有可能情况的协方差值,然后将它们放入一个矩阵”,构成协方差矩阵。(本教程假设读者们对矩阵很熟悉并且知道如何去定义矩阵)。因此,一组n维数组的协方差矩阵的定义如下:
其中,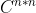 表示一个n行n列的矩阵,
表示一个n行n列的矩阵,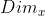 表示第x维。这一串复杂的公式(ugly looking formula)的意思是,如果你有一组n维的数据集,那么得到的是一个n行n列的协方差矩阵,矩阵中的每一个元素值是通过计算两个不同维度的协方差得到的(矩阵的位置跟协方差的组合有对应关系)。例如,第2行,第3列位置的元素值是通过计算第2维和第3维之间的协方差得到的。
表示第x维。这一串复杂的公式(ugly looking formula)的意思是,如果你有一组n维的数据集,那么得到的是一个n行n列的协方差矩阵,矩阵中的每一个元素值是通过计算两个不同维度的协方差得到的(矩阵的位置跟协方差的组合有对应关系)。例如,第2行,第3列位置的元素值是通过计算第2维和第3维之间的协方差得到的。
举一个例子,我们将虚构一组的3维数据集的协方差矩阵(使用x, y, z表示这三维)。得到一个3行3列的协方差矩阵,对应的元素值如下所示:
一些关键的注意点:一个注意点是,沿着协方差矩阵的主对角线方向,你会发现元素值是某一维和它本身的协方差,也就是这个维的方差。另一个注意点是,由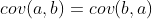 可知,协方差矩阵是一个对称阵。(协方差还有另一种定义形式,参考百度百科)
可知,协方差矩阵是一个对称阵。(协方差还有另一种定义形式,参考百度百科)
练习:
如下所示的一组2维数据集,计算出x和y维之间的协方差,并根据计算结果说明一下数据。

计算如下所示的一组3维数据集的协方差矩阵。

2.2 矩阵代数(Matrix Algebra)
本章节提供矩阵代数的背景知识有助于下文对PCA的理解。作者将侧重的介绍对于给定一个矩阵(方阵)的特征向量和特征值。同样的,作者假设读者们已经了解了一些矩阵的基础知识。
2.2.1 特征向量(Eigenvectors)
如读者们所知,假如两个矩阵的行数和列数满足矩阵相乘的条件(例如,C=AB,当矩阵A的列数等于矩阵B的行数时,A与B可以相乘),就可以将他们相乘。特征向量就是其中的一个特例,考虑如下2个“矩阵乘以向量”的式子。
式1:没有特征向量
式2:有一个特征向量
在第一个乘法式子(式1)里,矩阵乘以向量的结果并不是形如一个整数乘以原始向量(没有特征向量)。而在第二个乘法式子(式2)里相乘得到的结果是4乘以原始向量 特征向量来自于变换(矩阵)的性质(线性变换的特征向量是一个非简并的向量,其方向在该变换下不变。该向量在此变换下缩放的比例称为其特征值)。(A * V)想象有这么一个变换矩阵A作为左乘因子,将向量V映射到直线 y=x 上。然后你可以注意到是否有一个向量坐落于直线方程 y=x 上,这就是它自身的映射。此时,向量V(可以任意扩大它的倍数,因为向量的长度并不影响结果)就是变换矩阵A的一个特征向量。
特征向量还有其他什么性质呢?读者们首先应该知道特征向量必须是由一个方阵求解得到。但也不是所有的方阵都有特征向量。对于给定一个 n * n 的矩阵,并且该矩阵存在特征向量,那么这个矩阵有n个特征向量。类似的,对于给定一个 3 * 3 的矩阵(假设存在特征向量),那么这个矩阵有3个特征向量。
特征向量的另一个性质是,即使变换矩阵A乘以原始向量V =  之前,先将V扩大2倍,再将矩阵与扩大后的向量 V‘ 相乘,得到的结果仍然是变换矩阵的特征向量,且同样扩大了2倍,如下图所示。
之前,先将V扩大2倍,再将矩阵与扩大后的向量 V‘ 相乘,得到的结果仍然是变换矩阵的特征向量,且同样扩大了2倍,如下图所示。
向量与矩阵相乘前,乘以倍数2
变换矩阵乘以扩大了2倍的原始向量
这是因为,如果你对原始向量扩大n倍,意味着将向量变得更长但不改变向量的方向。最后,由变换矩阵得到的所有特征向量都是正交的,不管数据集有多少维,两两都相互垂直。这部分知识非常重要,因为这意味着你可以通过这些正交的特征向量来数据表达,而不用根据 x-y 坐标系。我们将在下文的PCA章节进行讨论。(参考:基与正交基,特征值与特征向量)
另一个读者们应该知道的重点是,“数学家们在求解特征向量时,他们更愿意去找到这些模正好为1的特征向量”。这是因为,如读者们所知,向量的大小并不影响这个向量是否为特征向量,但是方向就有影响。因此,为了标准化特征向量,当我们求得一个特征向量时,通常将它的模缩放为1,使得所有特征向量都有相同的模(模为1)。如下,通过一个例子加以验证。(此部分更详细的内容可参考:PCA数学原理)
向量  是一个特征向量,这个向量的模为:
是一个特征向量,这个向量的模为: ,然后我们将原始向量
,然后我们将原始向量  除以模
除以模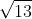 ,使得特征向量的模变为1,如下:
,使得特征向量的模变为1,如下:
那么,我们如何着手去找到这些神秘的特征向量呢?不幸的是,能够简单的进行求解的条件是你处理的对象是一个很小的矩阵,就像一个规模不大于 3*3 的方阵。对于求解规模较大方阵的特征向量,通常的方法是通过一些复杂的迭代方法进行求解(这些方法超出了本教程的范围,作者没做进一步的介绍)。如果读者们需要通过程序求解方阵的特征向量,可以找一个数学库(例如,Matlab,你只需要调用相关的函数即可,具体的实现过程这个库已经帮你完成了)。此外,有一个叫做“newmat”的数学工具包仅供读者参考:http://webnz.com/robert/。
想要进一步了解“关于如何求解一般情况下的特征向量,正交性”的读者们,可以参考由Howard Anton编著,John Wiley & Sons股份有限公司出版的教科书“基础线性代数 第五版”(ISBN 0-471-85223-6)。
2.2.2 特征值
特征值跟特征向量紧密相关,实际上,让我们回顾一下“2.2.1 特征向量”这节的2个例子,我们可以注意到这2个例子中,“相同的方阵A,分别乘以原始向量 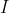 以及扩大2倍后的向量
以及扩大2倍后的向量 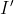 ,最后得到的特征向量前面的系数是一样的”。在这2个例子中,得到的系数都是4,4就是这个这个特征向量对应的特征值。在方阵A乘以向量V之前,无论我们先对向量V乘上一个多大的系数(非零:线性代数中规定特征向量不可以为零向量)得到的V‘,最后得到的都会是4乘以 V‘ 。(特征值的定义:设A为n阶矩阵,若存在常数λ及n维非零向量x,使得Ax=λx,则称λ是矩阵A的特征值,x是A属于特征值λ的特征向量)
,最后得到的特征向量前面的系数是一样的”。在这2个例子中,得到的系数都是4,4就是这个这个特征向量对应的特征值。在方阵A乘以向量V之前,无论我们先对向量V乘上一个多大的系数(非零:线性代数中规定特征向量不可以为零向量)得到的V‘,最后得到的都会是4乘以 V‘ 。(特征值的定义:设A为n阶矩阵,若存在常数λ及n维非零向量x,使得Ax=λx,则称λ是矩阵A的特征值,x是A属于特征值λ的特征向量)
读者们可以发现特征向量和特征值是成对出现的。当你使用一个理想的程序库去计算特征向量时,同时你也会得到相应的特征值。
练习:
对于下列矩阵:
分别对下列的5个向量,判断是否为上述方阵的特征向量,如果是,求出该特征向量向量对应的特征值。
【补充】可以通过Matlab提供的“eig()”函数求解特征向量及其对应的特征值,如下所示:
close all; clc; clear; A = [3 0 1; -4 1 2; -6 0 -2]; [d, v] = eig(A) A * d - v * d

如上实验结果所示,方阵A求得2个特征向量 [0; 1; 0] 和[0; -1; 0] 对应的特征值都是1。而上述例子中所给的5个向量中,只有[0;1; 0]是方阵A的特征向量。值得注意的是:对于上述例子的求解方法,应该根据特征值和特征向量的定义进行求解,即根据是否满足“A*Vector = egienvalue*Vector”的形式,如果满足,则向量Vector是方阵A的特征向量,反之不是。
第3章:主成分分析(PCA)
最后,我们来到了主成分分析(PCA)这节。主成分分析是个什么东西呢?它是一种“识别数据中的模式,通过强调数据的异同(similarities and differences)的方式来表达数据”的方法。由于很难发现高维数据中的模式,对于图形表示法是不可用的,而PCA正是一种强大的数据分析工具。
PCA的另一个主要优势是,一旦你发现数据中的这些模式,你就可以通过减少维数来压缩数据(保留主成分的数据),而且不会损失太多的信息。这项技术(优势)运用在图像压缩上,后面章节会具体介绍。
本章将为读者们介绍“在一组数据集上实现主成分分析”所需的相关步骤。本文并不会详细介绍PCA这项技术为什么能起作用(下文中,作者没有具体给出计算过程,是直接给出结果),但是作者会尝试着提供“每个要点(步骤)会发生什么(有什么作用)”的解释,因此当读者们尝试着使用到PCA这项技术时,能够做出明确的决定。
3.1 理论方法(PCA的六大步骤)
步骤一:获取数据集
为了简单起见,本文将使用作者自己构造的数据集。这是一组2维的数据集,选择这样一组数据集是因为能够对其作图,更直观的显示PCA分析过程中的每一个步骤的效果。如下左图所示是本章的原始数据集Data和减去均值后的数据集DataAdjust,右图是对DataAdjust进行作图的效果图。


步骤二:减去均值
为了让PCA正常工作,必须将原始数据集中的每一维的所有元素值减去该维的均值(数据的标准化)。(此处的数据集是2维数据,即x-y)也就是说,所有的 值都减去
值都减去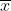 (
(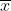 就是x维上所有元素值的均值),所有的
就是x维上所有元素值的均值),所有的  值都减去
值都减去 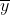 。这个过程使得我们得到一组均值为0的数据集。
。这个过程使得我们得到一组均值为0的数据集。
步骤三:计算协方差矩阵
这个步骤正如2.1.4节讨论过的计算协方差矩阵。因为这是一组2维数据集,所以将会得到一个 2 X 2 的协方差矩阵。在这里也是一样(无意外),因此作者直接给出结果,如下:
根据上述结果,由于协方差矩阵 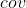 非对角线上的元素值是正数,我们可以推出变量 x 和 y 是正相关(同增同减)。
非对角线上的元素值是正数,我们可以推出变量 x 和 y 是正相关(同增同减)。
步骤四:计算协方差矩阵的特征向量及其对应的特征值
因为协方差矩阵是一个方阵,所以我们可以计算协方差矩阵的特征向量及其对应的特征值,这一步骤是非常重要的。特征向量及其对应的特征值告诉我们关于数据有用的信息,待会儿将展示给读者们看。在此期间,计算所得的特征向量和特征值如下所示:
注意:原文中给的特征向量的符号跟Matlab求得的不一样(这里给出Matlab求得的解),基于Matlab求解特征值和特征向量的代码如下所示:
cov = [0.616555556, 0.61544444; 0.616555556, 0.716555556]; % 协方差矩阵 [eigenvectors, eigenvalues] = eig(cov); % 求解特征向量及其对应的特征值
那么,这又是什么意思呢?如下图所示为标准化后的数据集(各维变量减去对应的均值),读者们可以发现这些数据中存在一个明显的模式(quite a strong pattern)。正如协方差矩阵所预期的一样,x和y两组变量的值呈正相关(同增同减)。在图的上方,作者也画出了对应的两个特征向量所表示的直线方程,它们以虚线的形式出现于坐标系的对角线。正如前面提到的一样,这一组特征向量相互垂直(正交),分别是图中斜率大于0以及斜率小于0的这两条虚线。但更重要的是,特征向量为我们提供了数据模式(此处的模式就是直线方程)的相关信息。首先让我们先关注这条经过数据集(标准化后)中心的特征向量对应的直线(斜率小于0那条直线),看起来像画了一条最拟合的直线吗(很明显不是)?这个特征向量告诉我们这两组数据集(应该指的是这两维的数据,x-y)是如何关联到这条直线。(这就是我们要找的直线,数据模式)而第二个特征向量为了我们提供了另一条直线(另一种数据模式),斜率大于0的那条线,坐标上所有的点沿着这条主线分布,但都以一定程度的距离偏离在这条主线的两侧。
所以,通过求解协方差矩阵的特征向量,我们已经能够提取出描述数据集的直线。现在,我们剩下的步骤包括,对数据进行转化,使其能够表达在特征向量对应的直线上。

步骤五:选择主成分,形成特征向量
接下来就是“数据压缩和降维”的到来。如果读者们仔细观察前几章讲到的特征向量和特征值,注意到求解得到的特征值是不一样的。实际上,最大的特征值对应的特征向量就是数据集的主成分。在本文的例子里,最大特征值对应的特征向量就是x-y坐标系中,斜率大于0的那条直线(此处论文好像有点问题,读者们可查看原文进一步验证)。这就是表达数据集维度之间的关系最有意义,最具代表性的模式。
通常来说,一旦从协方差矩阵中求解得到特征向量,下一步就是从大到小对特征值进行排序(此处要对应好特征向量和特征值),也就是对数据成分主次的排序(特征值越大,数据在该维就越有意义,信息量越大)。现在,如果读者们有需求的话,就可以忽略那些成分较小的维度。虽然你丢失了一些数据信息,但是忽略的这些维度的特征值很小,丢失的信息很少。如果你忽略一些成分(维度),最终得到的数据集的维数将比原始数据集的维数少(这就是数据降维)。(To be precise)确切地讲就是,如果你处理的原始数据集是n维,你将计算得到n个特征向量和特征值(有对应关系),然后你选择特征值前p(p < n)大的特征向量,忽略掉其他维度的数据,最后得到的数据集就是一组p维的数据集。
至此,读者们现在需要做的事情就是构造一个特征向量(fearue vector),其实就是由向量构成的一个矩阵。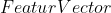 就是取前k大的特征值对应的eigenvectors,然后根据如下形式,将这k个向量以列的形式构成一个矩阵。
就是取前k大的特征值对应的eigenvectors,然后根据如下形式,将这k个向量以列的形式构成一个矩阵。
回到本文例子的数据集,通过求解,我们有2个特征向量 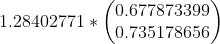 ,
, 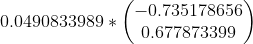 ,意味着我们有2种选择。如下所示,我们可以同时选择这2个特征向量作为
,意味着我们有2种选择。如下所示,我们可以同时选择这2个特征向量作为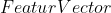 :
:
我们也可以选择忽略特征值较小的那维数据,仅仅保留特征值较大的那维数据,如下所示:
作者将在下一节展示以上两种结果。
(注:以上的 FeatureVector ,下文运用的时候,需要对其先进行转置)
步骤六:产生新的数据集(降维后)
这是PCA的最后一个步骤,也是最简单的。一旦我们选好了主成分(eigenvectors),并构造了特征向量(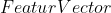 )后。我们首先对
)后。我们首先对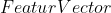 进行转置(得到1行2列或者2行2列的
进行转置(得到1行2列或者2行2列的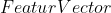 ),然后左乘以原始数据(已标准化且转置后,即2行n列),如下所示:
),然后左乘以原始数据(已标准化且转置后,即2行n列),如下所示:
其中,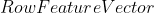 表示提取前k维主成分后构成的
表示提取前k维主成分后构成的 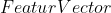 并进行转置后的矩阵(
并进行转置后的矩阵(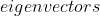 是按列进行存储,经过转置后的
是按列进行存储,经过转置后的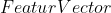 变成按行进行存储);
变成按行进行存储);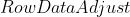 表示原始数据减去均值后再进行转置得到的结果,
表示原始数据减去均值后再进行转置得到的结果,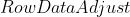 矩阵的每一列表示一组具体的数据项,如
矩阵的每一列表示一组具体的数据项,如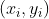 ,每一行表示独立的一个维(如,x维或者y维)。读者可能会因为这个步骤中出现的突然“转置”感到困惑,作者为此感到很抱歉,但如果读者们先对
,每一行表示独立的一个维(如,x维或者y维)。读者可能会因为这个步骤中出现的突然“转置”感到困惑,作者为此感到很抱歉,但如果读者们先对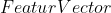 和
和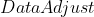 进行转置,这里的给出的公式将更加简单。而不是在
进行转置,这里的给出的公式将更加简单。而不是在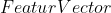 和
和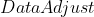 的右上方表上一个转置符号T(其实,翻译这里的时候,我不是很清楚这句话的用意);
的右上方表上一个转置符号T(其实,翻译这里的时候,我不是很清楚这句话的用意); 表示经过PCA算法后最终得到的数据集,其中每一列表示数据项
表示经过PCA算法后最终得到的数据集,其中每一列表示数据项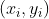 ,每一行表示具体的维(x维或者y维)。
,每一行表示具体的维(x维或者y维)。
行文至此,(降维后的  )我们将获得什么呢?仅仅根据我们选择的前k维特征向量,我们就可以得到原始数据。案例中的数据集有2维,包括x维和y维。读者们可以选择自己喜欢的两个维度来表示这些数据。如果这些维度是相互垂直(perpendicular)的,那么以这种方式表达数据会更有效。这就是为什么特征向量需要两两互相垂直会这么重要。我们已经改变了数据的表示形式(原来是基于x-y坐标系),现在是表示在2个特征向量上。当新的数据集进了降维的情况下,我们已经是忽略掉一些特征向量(
)我们将获得什么呢?仅仅根据我们选择的前k维特征向量,我们就可以得到原始数据。案例中的数据集有2维,包括x维和y维。读者们可以选择自己喜欢的两个维度来表示这些数据。如果这些维度是相互垂直(perpendicular)的,那么以这种方式表达数据会更有效。这就是为什么特征向量需要两两互相垂直会这么重要。我们已经改变了数据的表示形式(原来是基于x-y坐标系),现在是表示在2个特征向量上。当新的数据集进了降维的情况下,我们已经是忽略掉一些特征向量(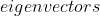 ),只保留了我们选择的前k个特征向量(
),只保留了我们选择的前k个特征向量(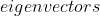 )。
)。
为了在数据上展示这些,作者已经对每一种可能的特征向量(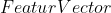 )完成了最后的变换(
)完成了最后的变换(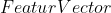 左乘
左乘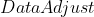 )。同时作者也对每一种情况的结果进行了转置,将数据转换回原始漂亮的表格格式(就是将更漂亮,更直观的表示格式)。作者还对最后得到的新数据进行作图,体现这些数据是怎样关联到成分(提取的前k个主成分)。
)。同时作者也对每一种情况的结果进行了转置,将数据转换回原始漂亮的表格格式(就是将更漂亮,更直观的表示格式)。作者还对最后得到的新数据进行作图,体现这些数据是怎样关联到成分(提取的前k个主成分)。
- 第一种情况(保留了所有的特征向量):如下左图表示经过
变换后的
,右图表示在新的坐标系(
)下绘制
这些数据坐标点,可以理解为原始数据和坐标系经过旋转一定的角度得到的。不难理解,这种情况下,没有损失任何数据。


- 第二种情况(只选择最大特征值对应的特征向量):如下图所示为降维后的数据集(从2维降到1维,和预期的一样)。读者们如果将这组数据与第一种情况的数据作比较,你会发现这组数据就是第一种情况那组数据的第一列,即对应 x 维的数据。

所以,如果你想对这组数据作图,如下图所示,得到的就是一维空间,而且图上 y=0 直线附近的这些坐标点恰好是 x 维空间上的位置(此时得到的坐标系,相当于y=0,主成分都在x轴上的数据)。我们已经抛掉另一维空间信息(y维),也就是另一个特征向量(值较小的那个特征向量被抛弃了)。

那么,到这里我们完成了什么呢?我们基本上已经对数据进行了变换,使得数据表达成它们之间的模式,本例中这些模式是“描述这些数据之间的关系的最拟合的直线”。这是非常有用的,因为我们现在已经将数据“根据这些直线(也就是特征向量eigenvector)对原始数据贡献信息的程度”进行组合分类。最初,我们有 x 和 y 坐标轴(完整的数据信息),但每个数据点的 x 值和 y 值实际上并不能确切告诉我们这个数据跟其他数据之间的关系(y值提供的信息量很少)。现在(降维后),数据点的坐标值(只有 x 值)告诉我们这个数据点适合于哪条趋势线(trend lines)。本例中,两个eigenvector都使用(转换)的情况下,我们仅仅简单的改变了数据,用求解得到的两个特征向量(eigenvectors)代替原本的 x-y 坐标系而已。但是,将特征值较小(y维,贡献小)的那一维去掉,只保留与特征值较大的那一维(x维)相关的数据的这种情况,就达到很好的降维效果,而且在丢失少量数据信息的情况下,用一维就能够很好的表示原始数据。
3.1.1 恢复旧数据
如果读者们使用 PCA 进行数据压缩,一定都会想要“恢复原始数据”,这个问题想必受到很多读者的关注,毕竟数据经过PCA变换后,仍是丢失了一些信息(下文有提供相关的案例)。这部分内容摘抄于http://www.vision.auc.dk/ sig/Teaching/Flerdim/Current/hotelling/hotelling.html。(这是原文提供的网址,但是好像进不去了- -)
那么,我们该如何恢复原始数据呢?在这之前,读者们应该知道只有在“将所有特征向量(eigenvectors)共同构成最终的变换矩阵”这种情况下,我们才能精确的恢复原始数据。如果最终的变换矩阵已经是经过降维(丢掉一些特征向量,比如上个例子中的 y 轴被丢弃),那么原始数据已经是丢失掉一些信息了,尽管是少量的信息。
回顾一下之前的“最终变换矩阵”,如下:
为了恢复原始数据,我们对上述公式做一下变形,得到如下公式:
其中,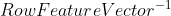 是
是 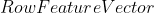 的逆(inverse)。当我们将所有的eigenvectors作为feature vector时(因为eigenvector和feature vector都翻译成“特征向量”,所以此处,我直接使用英文表示,加以区分),你会发现,原来矩阵 feature vector 的逆恰好等于feature vector的转置(当且仅当满足“feature vector矩阵的元素是数据集对应的单位特征向量,eigenvectors”这个条件的时候,成立。证明过程可以参考,这里)。这使得恢复数据变得更加容易,因为上述的表达式得到了改善,如下所示:
的逆(inverse)。当我们将所有的eigenvectors作为feature vector时(因为eigenvector和feature vector都翻译成“特征向量”,所以此处,我直接使用英文表示,加以区分),你会发现,原来矩阵 feature vector 的逆恰好等于feature vector的转置(当且仅当满足“feature vector矩阵的元素是数据集对应的单位特征向量,eigenvectors”这个条件的时候,成立。证明过程可以参考,这里)。这使得恢复数据变得更加容易,因为上述的表达式得到了改善,如下所示:
但是,为了恢复到最原始数据,我们还需要对每个维度的元素都加上相应的均值(因为,我们一开始的时候就对原始数据做了标准化,也就是各维度的元素都减去了均值)。所以,如下所示,是更完整的表达式:
这个公式对“并没有把所有的 eigenvectors 作为feature vector”这种情况也同样适用。所以即使当你丢弃一些eigenvector时,上述等式仍然可以得到正确的转换。
作者在本文中并不打算使用完整的feature vector(使用所有的eigenvector)演示数据恢复,因为这样得到的结果恰好就是我们一开始处理的数据集(最原始的数据)。然而,作者将做如下实验:“仅保留特征值较大的维度空间的情况,展示数据是如何丢失的”,如下图所示(降维后的数据),将图中的数据与最原始的数据作比较,你会发现只有沿着主成分eigenvector方向上的变量(x维)被保留了下来,沿着另一个eigenvector方向上的变量(y维)已经不见了。

练习:
- 求解协方差矩阵得到的特征向量能够带给我们什么(有什么作用)?
- 在PCA流程中,我们能够在“哪个步骤”决定压缩数据?会有什么影响?
- 找一个关于“PCA运用到面部识别”的案例并用图示法表示主要的eigenvectors(前k大的特征值对应的eigenvectors),可以通过“Eigenfaces”关键字进行搜索。
第4章:计算机视觉领域的应用(Application to Computer Vision)
本章将对“PCA在计算机视觉中的应用”进行概述。首先介绍图像通常是怎样表示的,然后介绍PCA能够帮助我们对这些图像做什么样的处理。在本章中,关于“面部识别(facial recognition)”的相关信息是来自于“Face Recognition: Eigenface, Elastic Matching, and Neural Nets”, Jun Zhang et al. Proceedings of the IEEE, Vol. 85, No. 9, September 1997。 表征信息来自于“Digital Image Processing”, Rafael C. Gonzalez and Paul Wintz, Addison-Wesley Publishing Company, 1987(这同样是关于“一般情况下,K-L变换更进一步的知识”一篇的很好的参考文献)。图像压缩的相关资料来自于“http://www.vision.auc.dk/ sig/Teaching/Flerdim/Current/hotelling/hotelling.html”(又进不去0- -,原文是2002年的,可能有些网址已经发生了改变,后续有找到的话,再更新分享给大家),这个参考网址也为我们提供一些关于“使用不同数量的eigenvector的图像重建”的案例。
4.1 (图像)表示方法(Representation)
在计算机视觉领域,当我们使用矩阵方法时,一定要考虑图像的表示形式。一个 N*N 的方阵可以被表示成一个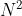 维的向量,如下所示:
维的向量,如下所示:
其中,图像中的像素以行为单位,一行接着一行被放置,形成一个一维的图像。例如,前N个元素(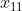 -
- )将被作为图像的第一行,接下来的N个元素(
)将被作为图像的第一行,接下来的N个元素(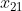 -
-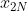 )作为第二行,以此类推。向量中的值反应图像的强度信息,或许就是一个简单的灰度值(对于灰度图像,就是对应灰度值)。
)作为第二行,以此类推。向量中的值反应图像的强度信息,或许就是一个简单的灰度值(对于灰度图像,就是对应灰度值)。
补充,如下矩阵所示,表示一个图像进行数字化的矩阵表示形式:
4.2 基于PCA寻找模式(模型)(PCA to find patterns)
假设我们有20张图像,每张图像由N个像素的高和N个像素的宽组成(N*N的矩阵)。对于每张图像,我们可以使用上一节的方法将其表示为一个图像向量。然后,我们可以将所有的图像(现在一张图像对应一个向量)放到一个大矩阵里面,形如:
以此作为我们使用PCA算法的第一步(现在处理的对象是一个由20张图像构成的大矩阵)。一旦使用PCA,我们要做的就是求解协方差矩阵得到特征向量(eigenvectors)。这(PCA)为什么有用呢?假设我们想实现面部识别,原始的数据集是人脸图像。问题是,给定一张新的人脸图像,识别出这张新图像对应原始数据图像中的哪一类人脸图像,也就是根据人脸图像信息进行分类(注意,这张新图像并不是来自于我们一开始所给的那20张图像)?这个问题在计算机视觉的解法是,基于PCA分析得到的新坐标系下,测量新的人脸图像与已知的20张人脸图像之间的区别,而不是在原来的坐标系。
事实证明经过PCA算法得到的新的坐标系更有利于识别人脸,这是因为PCA算法告诉我们原始图像(数据)之间的差异(differences and similarities)。PCA算法确定了数据中的统计模型。
因为所有的向量都是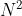 维,所以我们将得到
维,所以我们将得到 个特征向量(eigenvector)。实际上,我们也可以丢弃一些意义不大的eigenvectors(只保留特征值前k大对应的eigenvectors),识别的效果同样不错。
个特征向量(eigenvector)。实际上,我们也可以丢弃一些意义不大的eigenvectors(只保留特征值前k大对应的eigenvectors),识别的效果同样不错。
4.3 基于PCA的图像压缩(PCA for image compression)
使用PCA算法进行图像压缩又称为Hotelling 变换或者K-L变换。假如我们有20张图像,每张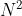 个像素。我们可以构造
个像素。我们可以构造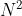 个向量,每个向量20维,每一维对应这20张图像中同一个像素的强度值,下文我(博主)将补充说明。这一点与上一个例子的大不同,上一个例子是构成的向量vector中的每个元素都是对应不同的像素,而现在这个例子构成的每个向量(
个向量,每个向量20维,每一维对应这20张图像中同一个像素的强度值,下文我(博主)将补充说明。这一点与上一个例子的大不同,上一个例子是构成的向量vector中的每个元素都是对应不同的像素,而现在这个例子构成的每个向量(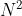 个)的元素对应20张图像相同的一个像素值。
个)的元素对应20张图像相同的一个像素值。
---------------
补充说明: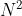 个20维的向量
个20维的向量
- 第1个向量形如:
- 第2个向量形如:
- 第
个向量形如:
其中,每个向量中有20个像素值,比如第1个向量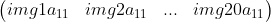 的20个元素值分别对应从第一张图像到第20张图像的第一个像素值
的20个元素值分别对应从第一张图像到第20张图像的第一个像素值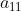 ,以此类推。
,以此类推。
---------------
现在开始对这组数据使用PCA算法。我们将得到20个特征向量(eigenvectors),因为每个vector都是20维。为了压缩数据,我们可以使用特征值前15大对应的15个eigenvector作为变换矩阵。最后得到的数据集只剩下15维,减少了1/4的空间。然而,但需要重构原始数据集时,得到的图像将丢失一些信息。PCA是一项有损信息的压缩技术,因为解压后的图像并不跟原始数据完全一样,通常更糟(差异更大)。
5. 博主补充:PCA实例
- 原始数据集:
,使用PCA算法将这组二维数据降维成一维数据。
- 因为这个矩阵的每行已经是零均值,这里我们直接求协方差矩阵,过程如下:
- 然后求其特征值和特征向量,具体求解方法不再详述,可以参考相关资料。求解后特征值如下所示:
- 其对应的特征向量分别是:
- 其中对应的特征向量分别是一个通解,
和
可取任意实数。那么标准化后的特征向量(是一个单位特征向量)为 :
- 因此我们的矩阵P是:
- 可以验证协方差矩阵C的对角化:
- 最后我们用P的第一行乘以数据矩阵,就得到了降维后的表示:
- 降维投影结果如下图:

注:本例(来自于文章“PCA数学原理”)在求解协方差矩阵的过程中,协方差的分母是用n表示。但是我们在本教程中提到,处理样本而非总体的时候,我们更倾向于选择 (n-1) ,即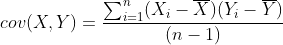 。在此,我们保留以上例子,但为了让例子更贴近本教程,博主使用Matlab对该例子进行求解,协方差的分母使用的是 (n-1),代码和实验结果如下所示:
。在此,我们保留以上例子,但为了让例子更贴近本教程,博主使用Matlab对该例子进行求解,协方差的分母使用的是 (n-1),代码和实验结果如下所示:
- 数据集还是上个例子的数据集:
- 求解协方差矩阵,代码如下:
close all;
clc;
clear;
%% PCA案例
X = [-1,-1,0,2,0];
Y = [-2,0,0,1,1];
mean_X = mean(X);
mean_Y = mean(Y);
n = 5;
sum_xy = 0;
sum_yx = 0;
sum_xx = 0;
sum_yy = 0;
for i = 1:5
sum_xy = sum_xy + (X(i) - mean_X) * (Y(i) - mean_Y);
sum_yx = sum_yx + (Y(i) - mean_Y) * (X(i) - mean_X);
sum_xx = sum_xx + (X(i) - mean_X) * (X(i) - mean_X);
sum_yy = sum_yy + (Y(i) - mean_Y) * (Y(i) - mean_Y);
end
cov_xx = sum_xx / (n-1)
cov_xy = sum_xy / (n-1)
cov_yy = sum_yy / (n-1)
cov_yx = sum_yx / (n-1)
-- 协方差矩阵: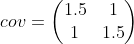
- 根据协方差矩阵求解特征向量和特征值:
cov_test = cov(X,Y); % 协方差矩阵 [eigenvectors eigenvalues] = eig(cov_test); %特征向量和特征值
-- 特征值:0.5 和 2.5
- 选择最大特征值(此处为2.5)对应的特征向量作为feature vector:
- 根据公式
,求解降维后的新数据集:(从2维降到1维)
X = [-1,-1,0,2,0]; Y = [-2,0,0,1,1]; % 特征向量 featurevector = [0.7071;0.7071]; % 直接提取最大特征值对应的特征向量 RowFeatureVector = featurevector‘; % 转置 RowAdjustData = [X;Y]; FinalData = RowFeatureVector * RowAdjustData
附录A
实现代码:
本文代码是基于Scilab(一款开源的软件)实现的。与Matlab类似,SCILAB也是一种科学工程计算软件,其数据类型丰富,可以很方便地实现各种矩阵运算与图形显示,能应用于科学计算、数学建模、信号处理、决策优化、线性/非线性控制等各个方面。作者使用以下代码生成了本文中的所有案例。代码中除了第一部分的宏(macro)以外,其余部分都是作者自己完成的。
注:这部分代码,本人尚未进一步验证,后续验证了再更新。
% This macro taken from
% http://www.cs.montana.edu/?harkin/courses/cs530/scilab/macros/cov.sci
% No alterations made
% Return the covariance matrix of the data in x, where each column of x
% is one dimension of an n-dimensional data set. That is, x has x columns
% and m rows, and each row is one sample.
%
% For example, if x is three dimensional and there are 4 samples.
% x = [1 2 3;4 5 6;7 8 9;10 11 12]
% c = cov (x)
function [c]=cov (x)
% Get the size of the array
sizex=size(x);
% Get the mean of each column
meanx = mean (x, ‘r‘);
% For each pair of variables, x1, x2, calculate
% sum ((x1 - meanx1)(x2-meanx2))/(m-1)
for var = 1:sizex(2),
x1 = x(:,var);
mx1 = meanx (var);
for ct = var:sizex (2),
x2 = x(:,ct);
mx2 = meanx (ct);
v = ((x1 - mx1)‘ * (x2 - mx2))/(sizex(1) - 1);
cv(var,ct) = v;
cv(ct,var) = v;
% do the lower part of c also.
end
end
c=cv;
% This a simple wrapper function to get just the eigenvectors
% since the system call returns 3 matrices
function [x]=justeigs (x)
% This just returns the eigenvectors of the matrix
[a, eig, b] = bdiag(x);
x= eig;
% this function makes the transformation to the eigenspace for PCA
% parameters:
% adjusteddata = mean-adjusted data set
% eigenvectors = SORTED eigenvectors (by eigenvalue)
% dimensions = how many eigenvectors you wish to keep
%
% The first two parameters can come from the result of calling
% PCAprepare on your data.
% The last is up to you.
function [finaldata] = PCAtransform(adjusteddata,eigenvectors,dimensions)
finaleigs = eigenvectors(:,1:dimensions);
prefinaldata = finaleigs‘*adjusteddata‘;
finaldata = prefinaldata‘;
% This function does the preparation for PCA analysis
% It adjusts the data to subtract the mean, finds the covariance matrix,
% and finds normal eigenvectors of that covariance matrix.
% It returns 4 matrices
% meanadjust = the mean-adjust data set
% covmat = the covariance matrix of the data
% eigvalues = the eigenvalues of the covariance matrix, IN SORTED ORDER
% normaleigs = the normalised eigenvectors of the covariance matrix,
% IN SORTED ORDER WITH RESPECT TO
% THEIR EIGENVALUES, for selection for the feature vector.
%
% NOTE: This function cannot handle data sets that have any eigenvalues
% equal to zero. It’s got something to do with the way that scilab treats
% the empty matrix and zeros.
function [meanadjusted,covmat,sorteigvalues,sortnormaleigs] = PCAprepare (data)
% Calculates the mean adjusted matrix, only for 2 dimensional data
means = mean(data,‘r‘);
meanadjusted = meanadjust(data);
covmat = cov(meanadjusted);
eigvalues = spec(covmat);
normaleigs = justeigs(covmat);
sorteigvalues = sorteigvectors(eigvalues‘, eigvalues‘);
sortnormaleigs = sorteigvectors(eigvalues‘, normaleigs);
% This removes a specified column from a matrix
% A = the matrix
% n = the column number you wish to remove
function [columnremoved] = removecolumn(A,n)
inputsize = size(A);
numcols = inputsize(2);
temp = A(:,1:(n-1));
for var = 1:(numcols - n)
temp(:,(n+var)-1) = A(:,(n+var));
end,
columnremoved = temp;
% This finds the column number that has the
% highest value in it’s first row.
function [column] = highestvalcolumn(A)
inputsize = size(A);
numcols = inputsize(2);
maxval = A(1,1);
maxcol = 1;
for var = 2:numcols
if A(1,var) > maxval
maxval = A(1,var);
maxcol = var;
end,
end,
column = maxcol
% This sorts a matrix of vectors, based on the values of
% another matrix
%
% values = the list of eigenvalues (1 per column)
% vectors = The list of eigenvectors (1 per column)
%
% NOTE: The values should correspond to the vectors
% so that the value in column x corresponds to the vector
% in column x.
function [sortedvecs] = sorteigvectors(values,vectors)
inputsize = size(values);
numcols = inputsize(2);
highcol = highestvalcolumn(values);
sorted = vectors(:,highcol);
remainvec = removecolumn(vectors,highcol);
remainval = removecolumn(values,highcol);
for var = 2:numcols
highcol = highestvalcolumn(remainval);
sorted(:,var) = remainvec(:,highcol);
remainvec = removecolumn(remainvec,highcol);
remainval = removecolumn(remainval,highcol);
end
sortedvecs = sorted;
% This takes a set of data, and subtracts
% the column mean from each column.
function [meanadjusted] = meanadjust(Data)
inputsize = size(Data);
numcols = inputsize(2);
means = mean(Data,‘r‘);
tmpmeanadjusted = Data(:,1) - means(:,1);
for var = 2:numcols
tmpmeanadjusted(:,var) = Data(:,var) - means(:,var);
end
meanadjusted = tmpmeanadjusted
附录B:本文相关的Matlab作图代码
1. 【协方差部分】H和M的关系图
%% ctrl + R 注释
%% ctrl + T 取消注释
close all;
clc;
clear;
fontsize = 11;
figure;
% x = 0:0.00025:1;
% y = x.*sin(10*3.14.*x)+2;
% plot(x,y)
x = [9 15 25 14 10 18 0 16 5 19 16 20];
y = [39 56 93 61 50 75 32 85 42 70 66 80];
plot(x, y, ‘o‘);
xlabel({‘H / 小时‘}, ‘FontSize‘,fontsize);
ylabel({‘M / 分数‘}, ‘FontSize‘,fontsize);
h = legend([‘H(学习时间)和M(获得分数)的关系‘, sprintf(‘\n‘)], ‘location‘, ‘best‘);
grid on;
set(h, ‘Box‘, ‘off‘);
参考文献
- PCA数学原理:http://www.360doc.com/content/13/1124/02/9482_331688889.shtml
- 杜洪,夏欣,琚生根,王能。基于PCA图像压缩算法研究与实现:http://www.cnki.com.cn/Article/CJFDTotal-SCDX201405009.htm
- 本文对应的原文:【PDF】http://pan.baidu.com/s/1nvNPJ4H | 【文章出处】https://arxiv.org/abs/1404.1100
- 博主的CSDN主页:http://blog.csdn.net/houchaoqun_xmu
- 【Latex】制作演示文档或者课程报告-常见用法(一)
- 【Latex】制作演示文档或者课程报告 - 制作演示文档(二)
- 【Latex】制作演示文档或者课程报告 - 制作课程报告(三)
- TSP_旅行商问题 - 蛮力法DFS(一)
- TSP_旅行商问题 - 模拟退火算法(三)
- TSP_旅行商问题 - 遗传算法(四)
以上是关于A tutorial on Principal Components Analysis | 主成分分析(PCA)教程的主要内容,如果未能解决你的问题,请参考以下文章