一元多项式的运算

Posted 2020-06-13

以一元多项式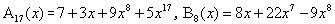加法运算为例:

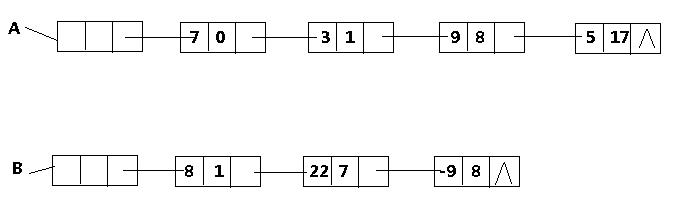
A,B可用线性链表可以表示为:

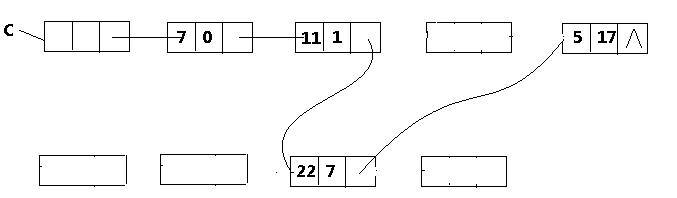
“和多项式”链表如下(图中的长方框表示已经被释放的结点):

#include <stdio.h>
#include <stdlib.h>
typedef struct Polyn{
    int data;
    int index;
    struct Polyn *next;
}Polyn,*Polynlist;
void CreatPolyn(Polynlist &p,int m)//输入m项的系数和指数,建立一元多项式P
{    
    //有头结点
    Polyn *q=p;
    for(int i=0;i<m;i++)
    {
        q->next=(Polyn*)malloc(sizeof(Polyn));
        q=q->next;
//        printf("第%d项系数、指数:",i+1);
        scanf("%d%d",&q->data,&q->index);
    }
    q->next=0;
}
void PrintPolyn(Polynlist &p)//打印一元多项式P
{
    Polyn *q=p->next;
    //(x^0)和(x^1)要做特别处理
    if(q->index == 0)                                                                                    
    {
        printf("%d",q->data);
        //可能第二项指数为x
        q=q->next;
        if(q && q->index == 1)
        {
            if(q->data != 1)
                printf("%+dx",q->data);//正数则在前面加+,否则不加
            else
                printf("+x");
            q = q->next;
        }
    }
    else if(q->index == 1){
        if(q->data != 1)
            printf("%dx",q->data);
        else
            printf("x");
        q = q->next;
    }
    else{
        printf("%dx^%d",q->data,q->index);
        q = q->next;
    }
    while(q)
    {
        printf("%+dx^%d",q->data,q->index);
        q=q->next;
    }
    printf("\n");
}
void CopyPolyn(Polynlist &q,Polyn *r)//空指针必须引用去创建,新开辟结点链表并复制(数据域和指针域)
{
    q = (Polyn *)malloc(sizeof(Polyn));
    Polyn *q1 = q,*r1 = r->next;
    while(r1)
    {
        q1->next = (Polyn *)malloc(sizeof(Polyn));
        q1 = q1->next;
        q1->data = r1->data;
        q1->index = r1->index;
        r1 = r1->next;
    }
    q1->next = NULL;
}
void ShowMenu()
{
    printf("\t\t\t1.多项式相加\n");
    printf("\t\t\t2.多项式相减\n");
    printf("\t\t\t3.多项式相乘\n");
    printf("\t\t\t4.退出\n");
}
void AddPolyn(Polyn *p,Polyn *p1)//完成多项式相加运算,p=p+p1,并销毁p1
{
    Polyn *qa,*qb,*prior,*r;//设置prior是为B链表中的结点插入A链表用
    prior = p;
    qa = p->next;
    qb = p1->next;
    while(qa && qb)
    {
        if(qa->index < qb->index)
        {
            prior = qa;
            qa = qa->next;
        }
        else if(qa->index > qb->index){
            r = qb;
            qb = qb->next;
            //摘取qb到“和多项式”链表中
            r->next = qa;
            prior->next = r;
            //更新prior
            prior = r;
        }
        else{
            if(qa->data + qb->data != 0)
            {
                //修改qa所指结点的系数值,同时释放qb所指的结点
                qa->data = qa->data + qb->data;
                r = qb;
                qb = qb->next;
                free(r);
            }
            else{
                //释放指针qa和qb所指的结点
                r = qa;
                qa = qa->next;
                prior->next = qa;//衔接
                free(r);
                r = qb;
                qb = qb->next;
                free(r);
            }
        }
    }
    //B链表还有结点
    if(qb)
    {
        prior->next = qb;//此时qa已为空指针
    }
    free(p1);//释放B头结点
}
void reverse(Polyn *p)
{
    Polyn *q = p->next;
    while(q)
    {
        q->data = -(q->data);
        q = q->next;
    }
}
void DestroyPolyn(Polyn *r)
{
    Polyn *q;
    do{
        q = r;
        r = r->next;
        free(q);
    }while(r);
}
void AdjustPolyn(Polyn *r,int data,int index)//调整每一项
{
    Polyn *q = r->next;
    while(q)
    {
        q->data *= data;
        q->index += index;
        q = q->next;
    }
}
void SubtractPolyn(Polynlist &p,Polynlist &p1)//完成多项式相减运算,p=p-p1,并销毁p1
{
    reverse(p1);//将B链表的data域置反
    AddPolyn(p,p1);
}
void MultiplyPolyn(Polynlist &p,Polyn *p1)//完成多项式相乘运算,p=p*p1,并销毁p1
{
    Polyn *q,*r = NULL,*r1 = NULL;
    q = p1->next;
    //A(x)--》bi*A(x)*x^ei
    CopyPolyn(r,p);
    AdjustPolyn(r,q->data,q->index);
    q = q->next;
    while(q)
    {
        CopyPolyn(r1,p);
        AdjustPolyn(r1,q->data,q->index);
        AddPolyn(r,r1);//r1将被销毁
        r1 = NULL;//必须将r1置空
        q = q->next;
    }
    //r-->p，同时释放r链表
    DestroyPolyn(p);
    p = NULL;
    CopyPolyn(p,r);
    DestroyPolyn(r);
}
int main()
{
    int m;
    Polyn *p=(Polyn*)malloc(sizeof(Polyn));
    Polyn *p1=(Polyn*)malloc(sizeof(Polyn));
    Polyn *p2 = NULL,*p3 = NULL;
    printf("按升幂输入多项式A(x),B(x)的系数,指数\n");
    printf("A(x)的项数:");
    scanf("%d",&m);
    CreatPolyn(p,m);
    printf("A(x)=");
    PrintPolyn(p);
    printf("B(x)的项数:");
    scanf("%d",&m);
    CreatPolyn(p1,m);
    printf("B(x)=");
    PrintPolyn(p1);
    //保存A,B原始多项式,此处的复制是新开辟结点链表
    CopyPolyn(p2,p);
    CopyPolyn(p3,p1);
    system("pause");
    system("cls");
    printf("A(x)=");
    PrintPolyn(p);
    printf("B(x)=");
    PrintPolyn(p1);
    printf("选择以下一种操作方式:\n");
    ShowMenu();
    do{
        printf("请输入你的选择:");
        scanf("%d",&m);
        switch(m)
        {
        case 1:
            AddPolyn(p,p1);
            printf("A(x)+B(x)=");
            PrintPolyn(p);
            break;
        case 2:
            SubtractPolyn(p,p1);
            printf("A(x)-B(x)=");
            PrintPolyn(p);
            break;
        case 3:
            MultiplyPolyn(p,p1);
            printf("A(x)*B(x)=");
            PrintPolyn(p);
            break;
        default:
            exit(0);
        }
        fflush(stdin);
        DestroyPolyn(p);
        p1 = p = NULL;//此时的p、p1为游离指针,必须要置空
        CopyPolyn(p,p2);
        CopyPolyn(p1,p3);
    }while(1);
    return 0;
}

 运行结果截图:

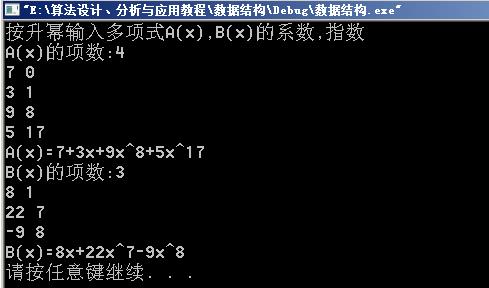
按Enter键之后