最小生成树—— Prim算法

Posted 2020-07-31

【问题描述】

N个村庄之间建立通信联络网，如何选择使得在经费最少的前提下实现全城通信.

 

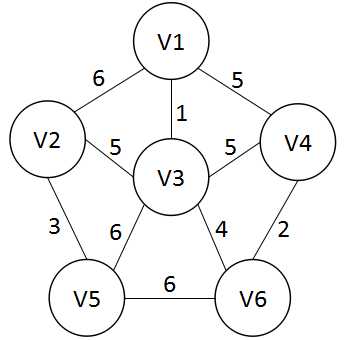
【思想分析】

假设U为所有实现通信的村庄的集合,从起点V1开始,此时U={V1},找到U与其它所有顶点权最小的边，并将V3纳入U,然后寻找U={V1,V3}与其他顶点的权最小的边，直到U={V1,V2,V3,V4,V5,V6}.

 

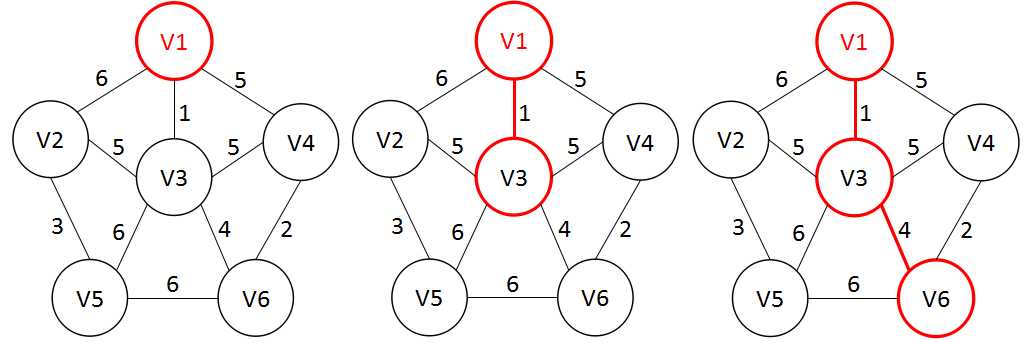
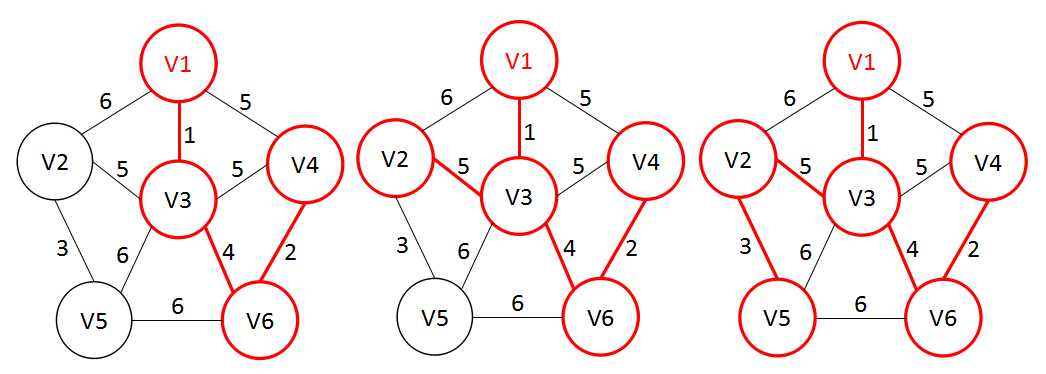
【代码实现】

首先选用邻接矩阵存储图，两个顶点之间用无穷大表示无连接，用0表示彼此实现通信，其余用权值。此时，选用一个辅助结构数组closedge，包含变量adjvex和lowcost。closedge[i]保存当前状态集合U与顶点Vi之间的信息，即

(closedge[i].adjvex , Vi)=closedge[i].lowcost

这样的话，如果从V1开始的，那么closedge初始状态为：

i	1	2	3	4	5	6
closedge[i].adjvex	V1	V1	V1	V1	V1	V1
closedge[i].lowcost		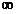6	1	5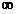

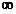这时找到最小lowcost=1，将V3纳入集合U中。记住每次纳入新的顶点都要更新一次closedge.

首先将closdge关于新顶点的最小权值lowcost设置为0，然后遍历所有顶点，如果新加入的顶点到某个顶点的边的权值比closedge中记录的更小，就用新加入顶点覆盖原数据（包括adjvex和lowcost）。因为找比如V3的加入使得closedge变为：

i	1	2	3	4	5	6
closedge[i].adjvex	V1	V3	V1	V1	V3	V3
closedge[i].lowcost		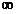5	0	5	6	4

 

重复直到所有的顶点都进入集合U，即完成全城通信.

【详细代码】经codeblocks-13.12调试

  1 #include<iostream>
  2 #define MAX_ARC 1001    //边的最大权值
  3 #define MAX_LINE 400    //图的最大边数
  4 #define MAX_NUM 20      //图的最大顶点数
  5 #define ERROR 0
  6 #define OK 1
  7 using namespace std;
  8 
  9 typedef int VertexType;//顶点类型
 10 
 11 typedef struct
 12 {
 13     VertexType vexs[MAX_NUM];//记录顶点
 14     int vexnum;
 15     int arcnum;
 16     int arcs[MAX_LINE][MAX_LINE];//记录图
 17 } MGraph;
 18 
 19 struct array
 20 {
 21     VertexType adjvex;
 22     int lowcost;
 23 } closedge[MAX_NUM]; //辅助数组，集合U与其他顶点vi的之间的最小边（adjvex,vi）=lowcost
 24 
 25 int LocateVex(MGraph G,VertexType u)//根据顶点返回它的位置
 26 {
 27     int i;
 28     for(i=1; i<=G.vexnum; i++)
 29     {
 30         if(G.vexs[i]==u)
 31         {
 32             return i;
 33         }
 34     }
 35     return ERROR;
 36 }
 37 
 38 int MiniSpanTree_PRIM(MGraph G,VertexType u)//从顶点u开始
 39 {
 40     int k,i,j;
 41     k=LocateVex(G,u);
 42     if(k==ERROR)
 43         return ERROR;
 44     //初始化closedge[]
 45     for(i=1; i<=G.vexnum; i++)
 46     {
 47         if(i!=k)
 48         {
 49             closedge[i].adjvex=k;//这里不是u
 50             closedge[i].lowcost=G.arcs[k][i];
 51         }
 52     }
 53     closedge[k].lowcost=0;//第k个顶点先进入集合U
 54     if(G.vexnum!=1)
 55         cout<<u<<"->";
 56     else
 57     {
 58         cout<<endl;
 59         return OK;
 60     }
 61 
 62     for(i=2; i<=G.vexnum; i++)//剩余vexnum-1个顶点
 63     {
 64         //在closedge[]中遍历并寻找下一个顶点
 65         int temp=MAX_ARC;//遍历记录最小边(adjvex,k)=lowcost
 66         k=0;
 67         for(j=1; j<=G.vexnum; j++)
 68         {
 69             if(closedge[j].lowcost>0&&temp>closedge[j].lowcost)
 70             {
 71                 temp=closedge[j].lowcost;
 72                 k=j;
 73             }
 74         }
 75         //将找到的顶点纳入集合U
 76         cout<<G.vexs[k];
 77         if(i!=G.vexnum)
 78             cout<<"->";
 79         else
 80             cout<<endl;
 81         //更新closedge
 82         closedge[k].lowcost=0;
 83         for(j=1; j<=G.vexnum; j++)
 84         {
 85             if(G.arcs[k][j]<closedge[j].lowcost)
 86             {
 87                 closedge[j].adjvex=k;
 88                 closedge[j].lowcost=G.arcs[k][j];
 89             }
 90         }
 91     }
 92     return OK;
 93 }
 94 
 95 int main()
 96 {
 97     MGraph G;
 98     VertexType a,b,u;
 99     int i,j,c;
100     cin>>G.vexnum>>G.arcnum;
101 
102     for(i=1; i<=G.vexnum; i++)
103     {
104         for(j=1; j<=G.vexnum; j++)
105         {
106             G.arcs[i][j]=MAX_ARC;
107         }
108     }
109 
110     for(i=1;i<=G.vexnum;i++)
111     {
112         cin>>G.vexs[i];
113     }
114 
115     for(i=1; i<=G.arcnum; i++)
116     {
117         cin>>a>>b>>c;
118         G.arcs[LocateVex(G,a)][LocateVex(G,b)]=c;
119         G.arcs[LocateVex(G,b)][LocateVex(G,a)]=c;//这句话千万记得加上
120     }
121     cin>>u;
122     MiniSpanTree_PRIM(G,u);
123     return 0;
124 }

【运行结果】不同VertexType的运行结果

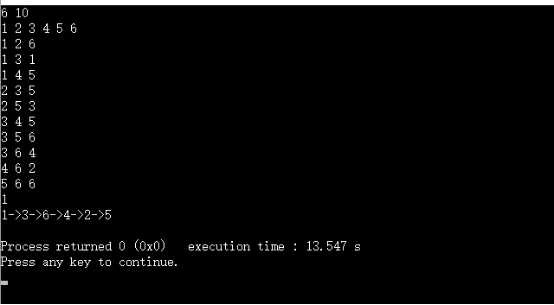
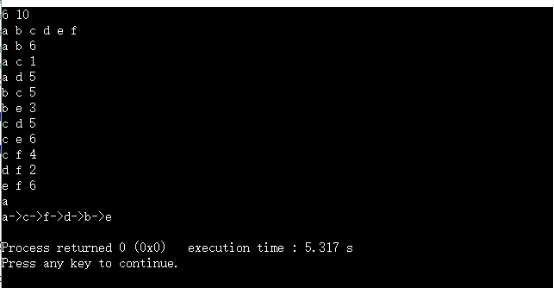
【后记】

算法思想提高智商，算法实现积累经验