P2403 [SDOI2010]所驼门王的宝藏

Posted 2022-12-12 gmsd

作为一个好（e）的（xin）的小紫题，很值得去做（虽然题目废话多，而且做法恶心）

题目描述

在宽广的非洲荒漠中，生活着一群勤劳勇敢的羊驼家族。被族人恭称为“先知”的Alpaca L. Sotomon是这个家族的领袖，外人也称其为“所驼门王”。所驼门王毕生致力于维护家族的安定与和谐，他曾亲自率军粉碎河蟹帝国主义的野蛮侵略，为族人立下赫赫战功。所驼门王一生财宝无数，但因其生性节俭低调，他将财宝埋藏在自己设计的地下宫殿里，这也是今天Henry Curtis故事的起点。Henry是一个爱财如命的贪婪家伙，而又非常聪明，他费尽心机谋划了这次盗窃行动，破解重重机关后来到这座地下宫殿前。

整座宫殿呈矩阵状，由R×C间矩形宫室组成，其中有N间宫室里埋藏着宝藏，称作藏宝宫室。宫殿里外、相邻宫室间都由坚硬的实体墙阻隔，由一间宫室到达另一间只能通过所驼门王独创的移动方式——传送门。所驼门王为这N间藏宝宫室每间都架设了一扇传送门，没有宝藏的宫室不设传送门，所有的宫室传送门分为三种：

1. “横天门”：由该门可以传送到同行的任一宫室；

2. “纵寰门”：由该门可以传送到同列的任一宫室；

3. “任意门”：由该门可以传送到以该门所在宫室为中心周围8格中任一宫室（如果目标宫室存在的话）。

深谋远虑的Henry当然事先就搞到了所驼门王当年的宫殿招标册，书册上详细记录了每扇传送门所属宫室及类型。而且，虽然宫殿内外相隔，但他自行准备了一种便携式传送门，可将自己传送到殿内任意一间宫室开始寻宝，并在任意一间宫室结束后传送出宫。整座宫殿只许进出一次，且便携门无法进行宫室之间的传送。不过好在宫室内传送门的使用没有次数限制，每间宫室也可以多次出入。

现在Henry已经打开了便携门，即将选择一间宫室进入。为得到尽多宝藏，他希望安排一条路线，使走过的不同藏宝宫室尽可能多。请你告诉Henry这条路线最多行经不同藏宝宫室的数目。

输入格式

输入文件sotomon.in第一行给出三个正整数N, R, C。

以下N行，每行给出一扇传送门的信息，包含三个正整数xi, yi, Ti，表示该传送门设在位于第xi行第yi列的藏宝宫室，类型为Ti。Ti是一个1~3间的整数，1表示可以传送到第xi行任意一列的“横天门”，2表示可以传送到任意一行第yi列的“纵寰门”，3表示可以传送到周围8格宫室的“任意门”。

保证1≤xi≤R，1≤yi≤C，所有的传送门位置互不相同。

输出格式

输出文件sotomon.out只有一个正整数，表示你确定的路线所经过不同藏宝宫室的最大数目。

输入输出样例

输入 #1复制

10 7 7
2 2 1
2 4 2
1 7 2
2 7 3
4 2 2
4 4 1
6 7 3
7 7 1
7 5 2
5 2 1

输出 #1复制

9

说明/提示

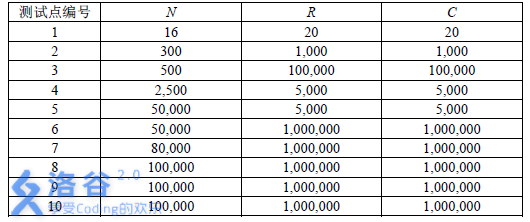
数据规模和约定：

--------------------------------------------分割线-----------------------------------------------

乍一看，普普通通的搜索题目，想着五六十分好拿，再剪剪枝就好了

但是看到这个极其恶心的数据范围，10^6，一个矩阵都存不下

再一看，一个简简单单的tarjan+DP

但是想想连接的边好像有点多

那我们就可以优化建边（这也是本题目最难的点，调了我一晚上）

 

那么由于各自的门的特殊性，我们应该分开建图，也就是三种算法，对于每一行的横天门，我们将其建成一个环，对于每一列的纵寰门，我们也将其建成一个环。因为我们知道：

每一行的所有横天门之间肯定都是相互通达，而每一列的所有纵寰门之间也肯定是相互通达的。所以我们可以说：

当你到达了某一行的一个横天门的时候，你就到达了这一行所有的横天门，当你到达了某一列的纵寰门的时候，你就到达了这一列所有的纵寰门。

于是我们完全可以将其建成一个环。而Tarjan的用途就来了。我们可以利用Tarjan将这两种环缩成点。而对于任意门本人并没有想到比暴力建边更好的方法，于是就暴力建边啦~~~。

但是好像还不够快，我们有

SORT

我们自然希望找横天门的时候越快越好，所以尽量的把横天门放在前面，所以cmp如下：

bool cmp1(node a,node b)
    if(a.x!=b.x)return a.x<b.x;
    if(a.opt==1)return 1;
    if(b.opt==1)return 0;
    return a.y<b.y;

那么查找纵寰门的时候也一样：

bool cmp2(node a,node b)
    if(a.y!=b.y)return a.y<b.y;
    if(a.opt==2)return 1;
    if(b.opt==2)return 0;
    return a.x<b.x;

好，已经排好了序，接下来就是巧妙的连边，我们有first表示每一次循环找的第一个，last表示上一个

那么，连边的代码：

sort(P+1,P+number+1,cmp1);
    first=last=1;
    for(int i=1;i<=number;i++)
        if(P[i].x!=P[i+1].x)
            if(first!=last)add(P[last].id,P[first].id);
            first=last=i+1;
        
        else
            if(P[last].opt==1)add(P[last].id,P[i+1].id);
            if(P[i+1].opt==1)last=i+1;
            if(P[first].opt!=1)last=first=i+1;
        
    

纵寰门也一样

那么接下来就是任意门（想到了哆啦A梦），这个我们用map存储

当然，这是c++选手的享受，其他语言可以用hash

那么代码如下:

for(int i=1;i<=number;i++)
        if(P[i].opt==3)
            for(int k=0;k<8;k++)
                int nx=P[i].x+dx[k],ny=P[i].y+dy[k];
                if(fh.count(pa(nx,ny)))
                  add(P[i].id,fh[pa(nx,ny)]);
            
        
    

好的，结束了这可怜的建边，接下来就用Tarjan找环

这个不用多说，直接上代码：

void Tarjan(int now)
    low[now]=dfn[now]=++deeth;res[now]=1;
    q[++top]=now;
    for(int i=head[now];i;i=nxt[i])
        int y=ver[i];
        if(!dfn[y])Tarjan(y),low[now]=min(low[now],low[y]);
        else if(res[y])low[now]=min(low[now],dfn[y]);
    
    if(dfn[now]==low[now])
        color[now]=++sum;res[now]=0;
        while(q[top]!=now)
            size[sum]++;
            res[q[top]]=0;color[q[top--]]=sum;
        
        size[sum]++;top--;
    

那么最后就是一个简单的DP了：

void dfs(int now,int fa)
    if(dp[now]>size[now])return;
    dp[now]=size[now];
    for(int i=head1[now];i;i=nxt1[i])
        int y=ver1[i];
        if(y==fa)continue;
        dfs(y,now);
        dp[now]=max(dp[now],dp[y]+size[now]);
    


for(int i=1;i<=sum;i++)
        if(in[i]==0)
            dfs(i,0);ans=max(ans,dp[i]);
        
    

那么AC代码就是：

  1 #include<bits/stdc++.h>
  2 using namespace std;
  3 #define pa pair<int,int>
  4 
  5 const int _=300002;
  6 int number,length,wide,first,last,size[_],dp[_],in[_];
  7 int ver[_*10],head[_*10],nxt[_*10],from[_*10],tot,ans=-1;
  8 int ver1[_*10],head1[_*10],nxt1[_*10],tot1;
  9 int dx[9]=-1,-1,-1,0,0,1,1,1,dy[9]=-1,0,1,-1,1,-1,0,1;
 10 int color[_],sum,low[_],dfn[_],q[_],top,deeth,res[_];
 11 struct nodeint x,y,opt,id;P[_];
 12 map<pa,int>fh;
 13 
 14 int read()
 15     int s=0,w=1;char ch=getchar();
 16     while(ch<‘0‘||ch>‘9‘)w=(ch==‘-‘)?-1:1,ch=getchar();
 17     while(ch>=‘0‘&&ch<=‘9‘)s=s*10+ch-‘0‘,ch=getchar();
 18     return s*w;
 19 
 20 
 21 void add(int x,int y)
 22     from[++tot]=x;ver[tot]=y;nxt[tot]=head[x];head[x]=tot;
 23 
 24 
 25 void ad(int x,int y)
 26     ver1[++tot1]=y;nxt1[tot1]=head1[x];head1[x]=tot1;
 27 
 28 
 29 bool cmp1(node a,node b)
 30     if(a.x!=b.x)return a.x<b.x;
 31     if(a.opt==1)return 1;
 32     if(b.opt==1)return 0;
 33     return a.y<b.y;
 34 
 35 
 36 bool cmp2(node a,node b)
 37     if(a.y!=b.y)return a.y<b.y;
 38     if(a.opt==2)return 1;
 39     if(b.opt==2)return 0;
 40     return a.x<b.x;
 41 
 42 
 43 void Tarjan(int now)
 44     low[now]=dfn[now]=++deeth;res[now]=1;
 45     q[++top]=now;
 46     for(int i=head[now];i;i=nxt[i])
 47         int y=ver[i];
 48         if(!dfn[y])Tarjan(y),low[now]=min(low[now],low[y]);
 49         else if(res[y])low[now]=min(low[now],dfn[y]);
 50     
 51     if(dfn[now]==low[now])
 52         color[now]=++sum;res[now]=0;
 53         while(q[top]!=now)
 54             size[sum]++;
 55             res[q[top]]=0;color[q[top--]]=sum;
 56         
 57         size[sum]++;top--;
 58     
 59 
 60 
 61 void dfs(int now,int fa)
 62     if(dp[now]>size[now])return;
 63     dp[now]=size[now];
 64     for(int i=head1[now];i;i=nxt1[i])
 65         int y=ver1[i];
 66         if(y==fa)continue;
 67         dfs(y,now);
 68         dp[now]=max(dp[now],dp[y]+size[now]);
 69     
 70 
 71 
 72 int main()
 73 //    freopen("precious.in","r",stdin);
 74 //    freopen("precious.out","w",stdout);
 75     number=read();length=read();wide=read();
 76     for(int i=1;i<=number;i++)
 77         P[i].x=read();P[i].y=read();P[i].opt=read();P[i].id=i;
 78         fh[pa(P[i].x,P[i].y)]=i;
 79     
 80     //-----------------------------------------------------
 81     for(int i=1;i<=number;i++)
 82         if(P[i].opt==3)
 83             for(int k=0;k<8;k++)
 84                 int nx=P[i].x+dx[k],ny=P[i].y+dy[k];
 85                 if(fh.count(pa(nx,ny)))
 86                   add(P[i].id,fh[pa(nx,ny)]);
 87             
 88         
 89     
 90     //-----------------------------------------------------
 91     sort(P+1,P+number+1,cmp1);
 92     first=last=1;
 93     for(int i=1;i<=number;i++)
 94         if(P[i].x!=P[i+1].x)
 95             if(first!=last)add(P[last].id,P[first].id);
 96             first=last=i+1;
 97         
 98         else
 99             if(P[last].opt==1)add(P[last].id,P[i+1].id);
100             if(P[i+1].opt==1)last=i+1;
101             if(P[first].opt!=1)last=first=i+1;
102         
103     
104     //------------------------------------------------------
105     sort(P+1,P+number+1,cmp2);
106     first=last=1;
107     for(int i=1;i<=number;i++)
108         if(P[i].y!=P[i+1].y)
109             if(first!=last)add(P[last].id,P[first].id);
110             first=last=i+1;
111         
112         else
113             if(P[last].opt==2)add(P[last].id,P[i+1].id);
114             if(P[i+1].opt==2)last=i+1;
115             if(P[first].opt!=2)last=first=i+1;
116         
117     
118     //------------------------------------------------------
119     for(int i=1;i<=number;i++)
120        if(!dfn[i])Tarjan(i);
121     for(int i=1;i<=tot;i++)
122         int x=from[i],y=ver[i];
123         if(color[x]==color[y])continue;
124         ad(color[x],color[y]);in[color[y]]++;
125     
126     for(int i=1;i<=sum;i++)
127         if(in[i]==0)
128             dfs(i,0);ans=max(ans,dp[i]);
129         
130     
131     cout<<ans;
132     return 0;
133