二分类逻辑回归及案例

Posted 2022-12-07 lucylucy

一、模型的构建

银行在放贷之前都会对客户做一个评估，来判定其是否有大概率会违约。这里我们用1表示其不会违约，用0表示会违约，假设影响因素有m个。

逻辑回归的目的是得到一个p（概率），如果给定一个临界值就可判断其属于哪一类，一般默认临界值为0.5，若p>0.5,则判定为第一类，既不会违约，若p<0.5,则判定为会违约。

sigmoid函数：    

 

 

 

 

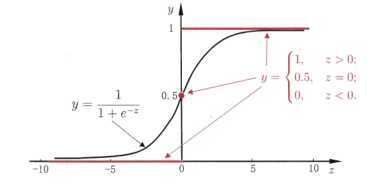
把z带入sigmoid函数：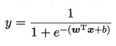  

变换得到逻辑回归的模型：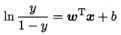

 

于是逻辑回归模型可以视为分对数变换下关于X的一个线性模型

若将y视为不违约的可能性，则1-y是违约的可能性

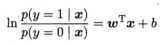
^于是有：

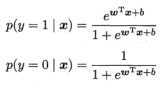
于是我们可以通过极大似然估计来估计：为了方便讨论：w^_TX+b可以简写为：β^TX

极大似然估计拟合逻辑回归模型的基本思想是：寻找一组β的估计，代入模型中，使所有不违约的人的值接近于1，而违约的人值接近于0。

1.构建似然函数：

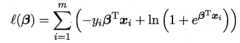
2.取对数，即对数拟然函数。

3.求偏导。令其为 0，解方程组，求得对应一组回归参数?? ?? 的最优解。

二、模型的解释：

ln（p_i / (1-p_i)）=β^TX

假设模型中只包含一个自变量：

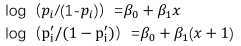
等式两侧同时取对数的反函数：

 

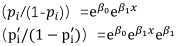
 两等式相除：

 

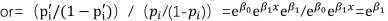
e^??₁ 表示为，x 每增加一个单位风险增加的倍数，如果??₁ 为 0.44，即e^??₁为 1.53，解释为其他变量处于控制状态下，x每增加一个单位，判断为不违约的概率比原来增加了1.53倍。

三、模型的评估：

roc曲线

1.混淆矩阵：

 

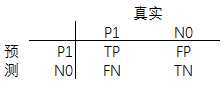
 TPR=TP/(TP+FN)

FPR=FP/(FP+TN)

 roc曲线：

auc：