分类算法 之 逻辑回归--理论+案例+代码
Posted 王小小小草
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了分类算法 之 逻辑回归--理论+案例+代码相关的知识,希望对你有一定的参考价值。
分类算法 之 逻辑回归–理论+案例+代码
标签(空格分隔): SPARK机器学习
1. 逻辑回归概述
1.1 概述
逻辑回归与线性回归类似,但它不属于回归分析家族(主要为二分类),而属于分类家族,差异主要在于变量不同,因此其解法与生成曲线也不尽相同。
逻辑回归是无监督学习的一个重要算法,对某些数据与事物的归属(分到哪个类别)及可能性(分到某一类别的概率)进行评估。
1.2 使用
在医学界,广泛应用于流行病学中,比如探索某个疾病的危险因素,根据危险因素预测疾病是否发生,与发生的概率。
比如探讨胃癌,可以选择两组人群,一组是胃癌患者,一组是非胃癌患者。因变量是“是否胃癌”,这里“是”与“否”就是要研究的两个分类类别。自变量是两组人群的年龄,性别,饮食习惯,等等许多(可以根据经验假设),自变量可以是连续的,也可以是分类的。
在金融界,较为常见的是使用逻辑回归去预测贷款是否会违约,或放贷之前去估计贷款者未来是否会违约或违约的概率。
在消费行业中,也可以被用于预测某个消费者是否会购买某个商品,是否会购买会员卡,从而针对性得对购买概率大的用户发放广告,或代金券等等,进行精准营销。
2. 逻辑分布(Logistic distribution)
设X是连续随机变量,X服从逻辑分布式指X具有下列分布函数和密度函数:
2.1 分布函数
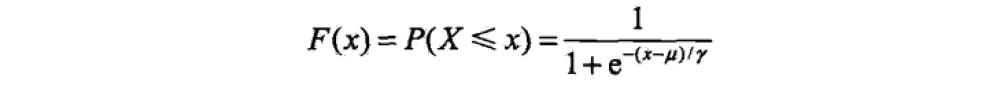
上述公式中,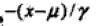 是一个标准化的过程,μ是均值(位置参数,决定分布的位置),
是一个标准化的过程,μ是均值(位置参数,决定分布的位置),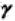 是标准差(形状参数,标准差越大则分布曲线越扁平,分布越不集中)
是标准差(形状参数,标准差越大则分布曲线越扁平,分布越不集中)
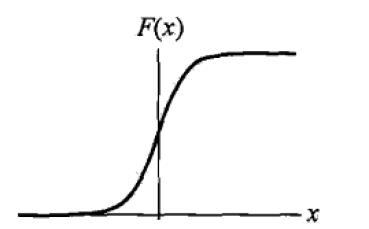
上图为逻辑分布函数的图形,是一条S型曲线(sigmoid curve)。该曲线以点(μ,1/2)为中心对称。曲线在中心附近增长速度较快,在两端增长速度较慢,形状参数的值越小,曲线在中心附近增长得就越快。
2.2 密度函数
密度函数是分布函数的一阶求导,公式与图形如下:
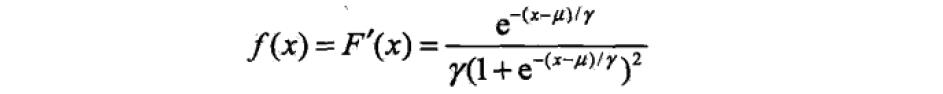
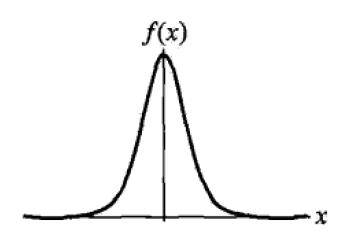
3. 二项逻辑回归模型(binomial logistic regression model)
二项逻辑回归模型是一种分类模型,有条件概率分布P(Y/X)表示,X为取数为实数,Y取值为0或1。研究已知X,求Y为1或0的概率。
3.1 二项逻辑回归模型
模型:
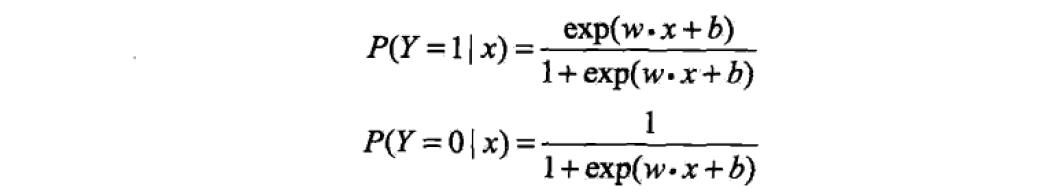
上述公式中,分别表示Y=1和Y=0的概率,Y是输出。
其中,x为输入变量,在机器学习中我们一般称之为feature,特征;w和b为参数,是我们接下来要去估计的,w为权值向量,b为偏置向量,w*x为w与x的内积。
根据以上公式,估计出参数后,输入已知的x值,便可以求出Y为1或0的概率了。两个概率相加为1.
逻辑回归会比较两个概率值的大小,然后将实例X分到概率较大的类别中。
简化模型:
有时,为了方便,我们将权值向量与输入向量将以扩充,即
w=(w0,w2,w3,…,wn,b)^T;
x=(x1,x2,x3,…,xn,1)^T.
^T表示矩阵的转置,那么上述模型可以简写为:
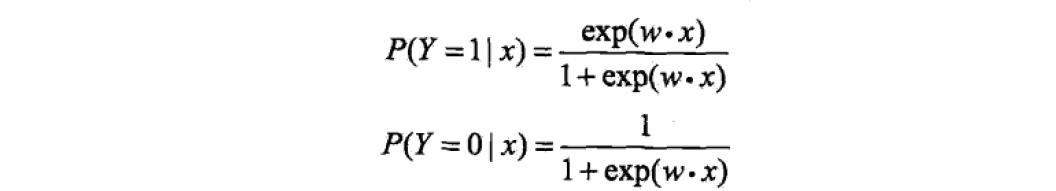
通常情况下,为了更简单只管,我们用z=w*x,那么模型也可以表达如下:
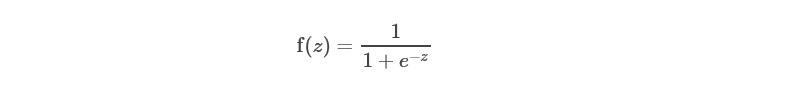
3.2 odds 和 log odds
odds
odds是指事件发生的概率与该事件不发生的概率的比值,如果事件发生的概率为P,不发生的概率为1-P,那么该事件的odds为
odds=P/(1-P)log odds
通常我们用log odds(logit)来表示:
logit(p)=log(p/(1-p))根据3.1节的逻辑回归模型,我们将发生的概率(P(Y=1/x))代入logit的p中。得到以下公式:
logit(p)=log(P(Y=1/x)/1-P(Y=1/x))
=w*x
=w0+w1*x1+w2*x2+...+wn*xn从以上公式可知输出Y=1的log odds是x的线性函数。
也就是说,通过逻辑回归模型,我们将线性函数w*x转变成了概率,从而达到分类的目的。
线性的值越接近于正无穷,概率的值就越接近1;线性的值越接近负无穷,概率的值就越接近0. 当w*x>0.5时,那么结果就是positive的,否则就是negative的
3.3 模型参数的估计
对于给定的数据集,我们可以采用极大似然估计法估计模型参数。
设:
P(Y=1/x)=π(x), P(Y=0/x)=1-π(x)似然函数为:
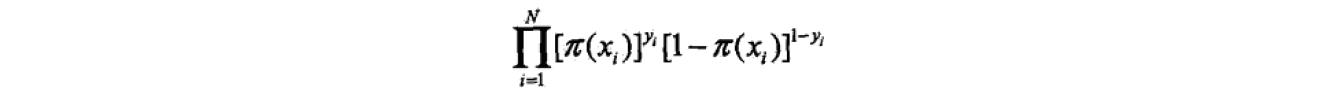
对数似然函数为:
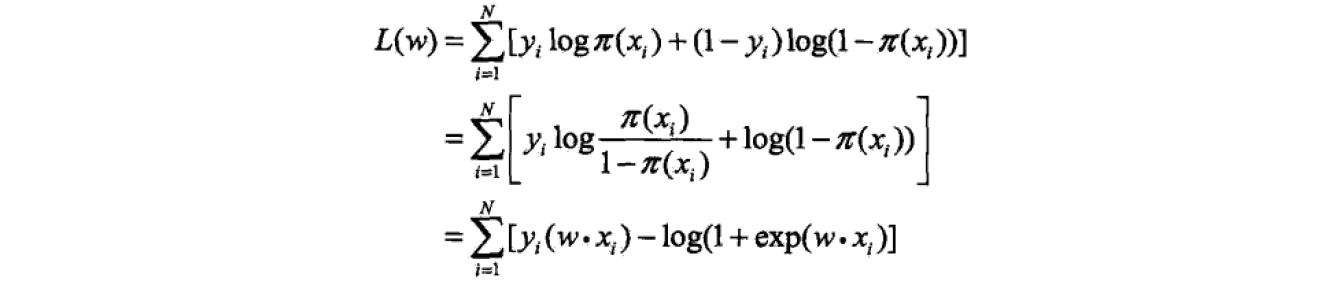
我们对以上对数似然函数L(w)求最大值,得到w的估计值,这是一个对目标函数L(w)求最优化的问题,通常采用梯度下降与拟牛顿法才求得最优解。
估计出w值后,我们就得到了完整的逻辑回归模型,使用这个模型去做预测。
4. 多项逻辑回归(multi-nominal logistic model)
逻辑回归不但可以应用到二分类中,也可以针对多个分类建立模型。
当Y有k个分类,Y=1,2,…,k,逻辑回归模型可如下构建:
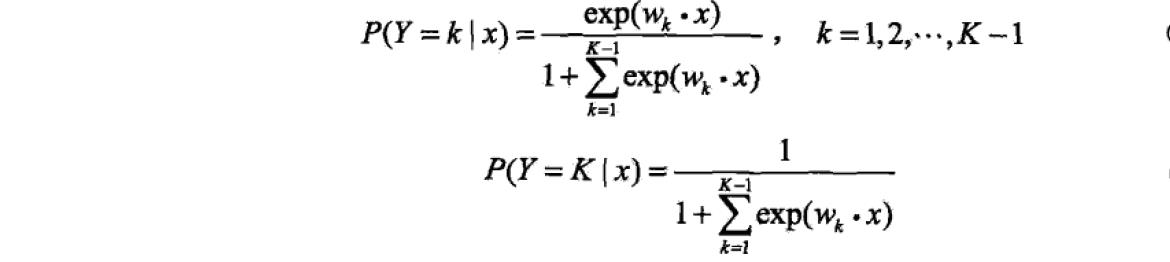
5. spark MLlib 逻辑回归案例(from example of 官方文档)
有两种最优化算法可以求解逻辑回归问题并求出最优参数:mini-batch gradient descent(梯度下降法),L-BFGS法。我们更推荐使用L-BFGS,因为它能更快聚合
5.1 导入逻辑回归需要的包:
import org.apache.spark.SparkContext
import org.apache.spark.mllib.classification.LogisticRegressionWithLBFGS, LogisticRegressionModel
import org.apache.spark.mllib.evaluation.MulticlassMetrics
import org.apache.spark.mllib.regression.LabeledPoint
import org.apache.spark.mllib.linalg.Vectors
import org.apache.spark.mllib.util.MLUtils5.2 创建新的实例
val conf =new SparkConf()
.setMaster("Local")
.setAppName("LogisticRegression")
val sc = new SparkContext(conf)5.3 以LIBSVM的格式加载数据
val data = MLUtils.loadLibSVMFile(sc, "data/mllib/sample_libsvm_data.txt")5.4 将数据分割成training dataset and test dataset,分别为60%,40%。seed为随机数池,每次随机抽数都不一样
// 随机分割traning dataset and test dataset
val splits = data.randomSplit(Array(0.6,0.4),seed = 11L)
//取分割后的第一个位数为training,然后缓存,因为等等又要使用到去建模
val training = split(0).cache
//取分割后的第二位数为testing dataset,不缓存,因为等等只会用于测试
val test = splits(1)5.5 运行tainning data构建模型
//新建一个logistic regression model;并且用LBFGS法去求最优参数
val model = new LogisticRegressionWithLBFGS()
.setNumClasses(10) //设置类型的数量
.run(traning) //将traning data放进模型5.6 使用以上创建的模型去估计test dataset
val predictionAndLabels = test.map case LabledPoint(label,features) =>
val prediction = model.predict(features)
(prediction,label)5.7 验证模型
//将上面test运算产生的数据(prediction,label)转化为MulticlassMetrics形式
val metrics = new MulticlassMetrics(predictionAndLabels)
//比较perdiction(通过模型预测出的应变量)和label(实际观测值的应变量),打印出精准度
val precision = metrics.precision
println("Precision = " + precision)5.8 保存模型,以后也可以直接下载使用该模型
model.save(sc,"myModelPath")
val samemodel = LogisicRegressionModel.load(sc,"myModelPath")6.Logistic regression案例二
6.1 一元逻辑回归
6.1.1 导入所需的包
import org.apache.spark.SparkContext
import org.apache.spark.mllib.classification.LogisticRegressionWithLBFGS, LogisticRegressionModel
import org.apache.spark.mllib.evaluation.MulticlassMetrics
import org.apache.spark.mllib.regression.LabeledPoint
import org.apache.spark.mllib.linalg.Vectors
import org.apache.spark.mllib.util.MLUtils6.1.2 建立模型
object LogisticRgressiom
val conf = new SparkConf() //创建环境变量
.setMaster("local") //设置运行在本地
.setAppName("LogisticRegression")//设置APP名字
val sc = new SparkConftext(conf) //创建实例
def main(args:Array[String])
val data = sc.textFile("//") //导入文件
val parseData = data.map line=> //预处理数据
val parts = lines.split('/') //将数据用/隔开
LabeledPoint = (parts(0).toDouble, //转化数据格式
vectors.dense(parts(1).map(_.toDouble))
.cache()
//建立模型,迭代次数设置为50
val model = LogisticRgressioneWithSGD.train(parseData,50)
//创建测试值
val target = vectors.dense(-1)
//根据以上建立的模型预测结果
val result = model.predict(target)
//打印结果
println(result)
6.1.3 模型的验证
MLlib中MulticlassMetrics类是对数据进行分类的类,其中包括各种方法,通过调用其中precision方法可以对数据进行验证。
object LogisticValidate
val conf = new SparkConf()
.setMaster("Local")
.setAppName("LogisticValidate")
val sc = new SparkContext(conf)
def main(arg:Array[String])
val data = sc.textFile("//") //读取数据集
//分割数据
val parseDate = data.randomSplit(Array(0.6,0.4),seed=11L)
val trainning = parseData(0).cache
val test = parseData(1)
//用tranning dataset训练模型
val model = LogisticRgressionWithSGD.train(trainning,50)
//打印创建的模型的参数(这个参数是用SGD法算出的)
println(model.weights)
//计算测试值
val PredictionAndLabels = test.map
case LabeledPonit(label,feature) =>
val prediction = model.predict(features)
(prediction,label) //存储测试值与真实值
//计算模型误差
val metrics = new MulticlassMetrics(predictionAndLabels)
val precision = metrics.precision
println("precision:" + precision)
以上是关于分类算法 之 逻辑回归--理论+案例+代码的主要内容,如果未能解决你的问题,请参考以下文章