旅行商问题分析（分支限界法）

Posted 2022-11-26 unicron

一、题目

 

 

 

二、思路

1、dfs

实验要求用多种思路完成，所以一开始就沿用了上一个实验马走棋盘的思路，添加了邻接矩阵来记录有向网的权值。总体思路还是DFS遍历搜索。

过程剪枝：

1、因为要求为最短路径，而一般情况总会存在多条可行路径，在判断过程中需要走过每一条路径才能知道该路径的长度，但如果已知一条可行路径的长度，在计算另一条路径的时候，若还未完成巡回但此时路径长度已经大于已知最短可行路径，那么这条路的最终长度就必定大于已知最短路径，此时就可以不必接下去计算当前路径。

2、之前得出的路径长度可以帮助之后的路径进行快速判断，如果我们尽早得出较短的可行路径，之后的工作也会进行得更快，由剪枝1引出剪枝2，每次选择到下一点路径长度最短的点前进，这样就能较快得到较短的可行路径。

 

2、分支限界法

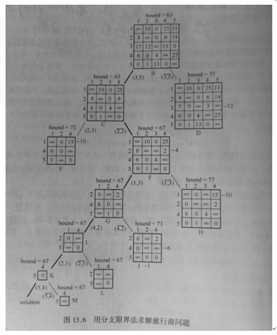
　　按照书本上教我们的思路来实现分支限界法，首先对邻接矩阵进行初始化，求出其的最小下界和对应的矩阵，然后以这个矩阵为根节点，开始进行类似二叉树的遍历。

　　在这个过程中，需要保持矩阵每行或每列都必须有一个以上的0，还需要一个函数来找出所有行中最小数中最大的。然后下一步就要决定是否走该行距离为0的点，如果选择走，就将点对应的行和列去掉，若不选择该点，则将该点置为无穷大。并比较选与不选情况下的下界变化，选择下界较小的情况继续进行递归处理，直到矩阵消失或剩下全为无穷大的不可到达点。

　　遇到问题：根据以上的逻辑，在实际解决过程中，出现了爆栈的情况，通过调试发现程序运行情况和书本上不一样，书本上有一些变化并没有说明清楚，那么就需要重新考虑程序的递归出口解决爆栈问题。

　　

 

 

最后根据书上的情况得修改为一共三种递归出口判断：

 

1、  若剩下的全是无穷远或0（默认跳过-1即不存在的）

2、  若剩下全是无穷远

3、  若剩下全是0

若满足以上任意一种判断，可以直接得出当前下界即为最短路径。

 

 

 

三、复杂度分析

以DFS为主要算法，O(e+v)

时间复杂度（V边数+ E顶点数）

实际复杂度比上述要小，因为在实际中并不会完整遍历所有可行路径。

 

分支限界法完成比较匆忙，代码中要多次循环遍历数组，存在诸多冗余，若不急循环，程序需要的步数及为顶点数，当不断的循环判断使得复杂度难以估计。

　　

三、实现代码

1、DFS

 1 public class Sell 
 2     static int[][] byGroup;// 邻接矩阵
 3     static int[] visit;// 0表示未访问 1表示访问
 4     static int N;// 点的个数
 5     static int minstep = 10000;// 最小步数
 6 
 7     class ToNode 
 8         int n;// 第n个点
 9         int L;//// 当前点到第n个点的距离
10 
11         public ToNode(int n, int l) 
12             this.n = n;
13             this.L = l;
14         
15     
16 
17     public static Comparator<ToNode> LComparator = new Comparator<ToNode>() // 优先队列的比較方法（到下一点的距离近到远
18         @Override
19         public int compare(ToNode tn1, ToNode tn2) 
20             return tn1.L - tn2.L;
21         
22     ;
23 
24     public void init() 
25         Scanner sc = new Scanner(System.in);
26         System.out.println("please int N:");
27         N = sc.nextInt();
28         byGroup = new int[N][N];
29         visit = new int[N];
30         for (int i = 0; i < N; i++) 
31             for (int j = 0; j < N; j++) 
32                 System.out.println("please int " + i + "-->" + j + " weight:");
33                 byGroup[i][j] = sc.nextInt();
34             
35         
36         DFS(0, 0);// 从0点开始
37     
38 
39     public void DFS(int n, int step) 
40         if (visit[n] != 0 || step >= minstep) // 当前点走过或当前已走长度大于已知最小可行长度
41             return;
42         
43         if (step != 0) // 第一次不赋值
44             visit[n] = 1;
45         
46         int flag = 1;
47         for (int k = 0; k < visit.length; k++) //判断是否走完所有点
48             if (visit[n] == 0) 
49                 flag = 0;
50                 break;
51             
52         
53         if (flag == 1 && n == 0) // 巡回完成的判断
54             System.out.println("巡回完成");
55             if (step < minstep) // 修改最短可行路径长度
56                 minstep = step;
57             
58             System.out.println("now donestep is:" + step);
59         
60         Queue<ToNode> nodePriorityQueue = new PriorityQueue<>(N, LComparator);// 每次來個優先隊列從小到大
61         for (int i = 0; i < byGroup[0].length; i++) 
62             if (i != n) 
63                 nodePriorityQueue.add(new ToNode(i, byGroup[n][i]));
64             
65         
66         while (!nodePriorityQueue.isEmpty()) // 回溯
67             ToNode tn = nodePriorityQueue.poll();
68             DFS(tn.n, step + tn.L);
69         
70     
71 
72     public static void main(String[] args) 
73         Sell s = new Sell();
74         s.init();
75         System.out.println("mini step is: " + minstep);
76     
77 

 

2、分支限界法

  1 public class Sell2 
  2     static int[][] group =   -2, 17, 7, 35, 18 ,  9, -2, 5, 14, 19 ,  29, 24, -2, 30, 12 ,
  3              27, 21, 25, -2, 48 ,  15, 16, 28, 18, -2  ;
  4     //-1表示不存在 -2表示无穷大到不了
  5     //static int[] flag;//初始化时判断
  6     static int[] hmin;// 每行对应的最小值
  7     static int bound;
  8     static int N = 5;
  9     static int[] hz = new int[5];// 用来记录该行是否已经全为-1
 10 
 11     public void init() // 初始化分支界限树的根节点
 12         Scanner sc = new Scanner(System.in);
 13         System.out.println("please int N:");
 14         // N = sc.nextInt();
 15         // group = new int[N][N];
 16         // group
 17         int[] flag = new int[N];
 18         hmin = new int[N];
 19         /*
 20          * for (int i = 0; i < N; i++)  for (int j = 0; j < N; j++) 
 21          * System.out.println("please int " + i + "-->" + j + " weight:"); group[i][j] =
 22          * sc.nextInt();  
 23          */
 24         int minh;
 25         for (int i = 0; i < group[0].length; i++) // 对行找最小并减去
 26             minh = 10000;
 27             for (int j = 0; j < group[0].length; j++) // 找当前行的最小值
 28                 if (group[i][j] != -1 && group[i][j] != -2 && group[i][j] < minh) 
 29                     minh = group[i][j];
 30                 
 31             
 32             bound += minh;
 33             for (int j = 0; j < group[0].length; j++) // 对每个数减去最小值并给flag赋值
 34                 if (group[i][j] != -1 && group[i][j] != -2) 
 35                     group[i][j] -= minh;
 36                     if (group[i][j] == 0) 
 37                         flag[j] = 1;
 38                     
 39                 
 40             
 41         
 42         int minl;
 43         for (int i = 0; i < flag.length; i++) 
 44             if (flag[i] != 1) // 第i列
 45                 minl = 10000;
 46                 for (int j = 0; j < group[0].length; j++) // 找当前列的最小值
 47                     if (group[j][i] != -1 && group[j][i] != -2 && group[j][i] < minl) 
 48                         minl = group[j][i];
 49                     
 50                 
 51                 bound += minl;
 52                 for (int j = 0; j < group[0].length; j++) // 对每个数减去最小值并给flag赋值
 53                     if (group[j][i] != -1 && group[i][j] != -2) 
 54                         group[j][i] -= minl;
 55                     
 56                 
 57             
 58         
 59     
 60 
 61     int minh = 10000;
 62     int bigMin = 0;// 所有行的最小数中最大的
 63 
 64     public void tree() 
 65         System.out.println(bound);
 66         int x, y = 0;// 每次对应的要或不要的点(x,y)
 67         // ********************************************************如果
 68         if (isDone1() == 1 || isDone2() == 0 || isDone3() == 0) // 判断完成
 69             System.out.println("okk");
 70             System.exit(1);
 71         
 72         x = findh();// 每行最小中最大的那个数的行
 73         for (int i = 0; i < N; i++) 
 74             if (group[x][i] == 0) 
 75                 y = i;
 76             
 77         
 78         if (need(x, y) > dontneed(x, y)) // 不要这个点
 79             group[x][y] = -2;
 80             // 检测每行是否都有0
 81             int havaz = 0;
 82             for (int i = 0; i < N; i++) 
 83                 havaz = 0;
 84                 for (int j = 0; j < N; j++) 
 85                     if (group[i][j] == 0) 
 86                         havaz = 1;// 有0
 87                     
 88                 
 89                 if (havaz == 0) // 第i行没0
 90                     bound += hmin[i];
 91                     for (int t = 0; t < N; t++) 
 92                         if (group[i][t] != -2 && group[i][t] != -1) 
 93                             group[i][t] -= hmin[i];
 94                         
 95                     
 96                 
 97             
 98             tree();// 递归
 99          else // 要这个点
100             hz[x] = 1;
101             if (group[y][x] != -1) 
102                 group[y][x] = -2;
103             
104             for (int i = 0; i < N; i++) // 把行消除
105                 group[x][i] = -1;
106             
107             for (int i = 0; i < N; i++) // 把列消除
108                 group[i][y] = -1;
109             
110             // 检测每行是否都有0
111             int havaz = 0;
112             for (int i = 0; i < N; i++) 
113                 if (hz[i] != 1) 
114                     havaz = 0;
115                     for (int j = 0; j < N; j++) 
116                         if (group[i][j] == 0) 
117                             havaz = 1;// 有0
118                         
119                     
120                     if (havaz == 0) 
121                         bound += hmin[i];
122                         for (int t = 0; t < N; t++) 
123                             if (group[i][t] != -2 && group[i][t] != -1) 
124                                 group[i][t] -= hmin[i];
125                             
126                             // group[i][t] -= hmin[i];
127                         
128                     
129                 
130 
131             
132             tree();// 递归
133         
134     
135 
136     // 要和不要这个点对应的bound
137     private int need(int x, int y) 
138         int needbound = bound;
139         for (int i = 0; i < N; i++) // 去掉行
140             group[x][i] = -1;
141         
142         for (int i = 0; i < N; i++) // 去掉列
143             group[i][y] = -1;
144         
145         // 检测每行是否都有0
146         int havaz;
147         for (int i = 0; i < N; i++) 
148             if (hz[i] != 1) 
149                 havaz = 0;
150                 for (int j = 0; j < N; j++) 
151                     if (group[i][j] == 0) 
152                         havaz = 1;// 有0
153                     
154                 
155                 if (havaz == 0) 
156                     needbound += hmin[i];
157                 
158             
159 
160         
161         return needbound;
162     
163 
164     private int dontneed(int x, int y) 
165         int dontneedbound = bound;
166         // 检测每行是否都有0 (去掉xy点)
167         int havaz;
168         for (int i = 0; i < N; i++) 
169             if (hz[i] != 1) 
170                 havaz = 0;
171                 for (int j = 0; j < N; j++) 
172                     if (i != x && j != y && group[i][j] == 0) 
173                         havaz = 1;// 有0
174                     
175                 
176                 if (havaz == 0) // 这行没0
177                     dontneedbound += hmin[i];
178                 
179             
180         
181         return dontneedbound;
182     
183 
184     private int findh() // 找出每行最小中最大的那个数在哪一行
185         int bigMin = 0;// 所有行的最小数中最大的
186         int minh, h = 0;
187         for (int i = 0; i < group[0].length; i++) // 对行找最小并减去
188             if (hz[i] != 1) 
189                 minh = 10000;
190                 for (int j = 0; j < group[0].length; j++) // 找当前行的最小值
191                     if (group[i][j] != -1 && group[i][j] != -2 && group[i][j] != 0 && group[i][j] < minh) 
192                         minh = group[i][j];
193                     
194                 
195                 hmin[i] = minh;// 更新当前行的最小值
196                 if (minh >= bigMin) 
197                     bigMin = minh;
198                     h = i;
199                 
200             
201 
202         
203         return h;
204     
205 
206     private int isDone1() // 判断是否完成
207         int zn = 0;// 0的个数 如果只剩一个0就完成
208         for (int i = 0; i < N; i++) 
209             for (int j = 0; j < N; j++) 
210                 if (group[i][j] == 0) 
211                     ++zn;
212                 
213             
214         
215         return zn;// 返回当前一共有几个0
216     
217 
218     private int isDone2() // 判断是否完成 如果除了-2就是0或-1 也算完成
219         int haszt = 0;// 不是0和-2的个数
220         for (int i = 0; i < N; i++) 
221             for (int j = 0; j < N; j++) 
222                 if (group[i][j] != 0 || group[i][j] != -2 || group[i][j] != -1) 
223                     ++haszt;
224                 
225             
226         
227         return haszt;
228     
229 
230     private int isDone3() // 判断3
231         int haszt = 0;// 不是-2的个数
232         for (int i = 0; i < N; i++) 
233             for (int j = 0; j < N; j++) 
234                 if (group[i][j] != -2) 
235                     ++haszt;
236                 
237             
238         
239         return haszt;
240     
241 
242     public static void main(String[] args) 
243         Sell2 s2 = new Sell2();
244         s2.init();
245         s2.tree();
246         System.out.println("bound:" + bound);
247     
248