[数学建模模拟退火法与旅行商问题]

Posted 2020-10-05

1.旅行商问题

旅行商问题(Traveling Salesman Problem,TSP)，是由爱尔兰数学家Sir William Rowan Hamilton和英国数学家Thomas Penyngton Kirkman在19世纪提出的数学问题。它的描述是这样的：一名商人要到若干城市去推销商品，已知城市个数和各城市间的路程（或旅费），要求找到一条从城市1出发，经过所有城市且每个城市只能访问一次，最后回到城市1的路线，使总的路程（或旅费）最小。现已证明它属于NP(Non-deterministic Polynomial---非确定多项式)难题。

若设城市数目为n时，那么组合路径数则为(n-1)!。当城市数量较小时，通过枚举法就可以找出最短的路径。随着城市数目的不断增大，组合路线数将呈指数级数规律急剧增长，以至达到无法计算的地步。此时，很难找到一个多项式时间复杂度的算法来求解该问题。

TSP是一个典型的组合优化问题，是诸多领域内出现的多种复杂问题的集中概括和简化形式，并且已成为各种启发式的搜索、优化算法的间接比较标准。

 

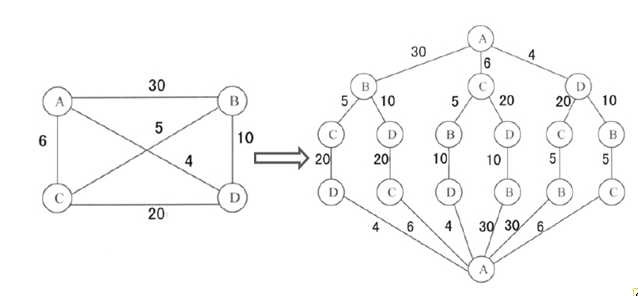
图1 当城市数量较少时，直接通过枚举求解

2.模拟退火法

2.1算法

模拟退火算法由KirkPatrick于1982提出^[7]，他将退火思想引入到组合优化领域,提出一种求解大规模组合优化问题的方法，对于NP-完全组合优化问题尤其有效。

模拟退火算法可以分解为解空间、目标函数和初始解3部分。其基本思想是：

(1)初始化：初始温度T(充分大)，初始解状态s(是算法迭代的起点)，每个T值的迭代次数L；

(2)对k=1，……，L做第(3)至第6步；

(3)产生新解s′；

(4)计算增量cost=cost(s′)-cost(s)，其中cost(s)为评价函数；

(5)若t′0则接受s′作为新的当前解，否则以概率exp(-t′/T)接受s′作为新的当前解；

(6)如果满足终止条件则输出当前解作为最优解，结束程序。终止条件通常取为连续若干个新解都没有被接受时终止算法；

(7)T逐渐减少，且T趋于0，然后转第2步运算。

2.2 参数选择

（1）温度T的初始值设置。

温度T的初始值设置是影响模拟退火算法全局搜索性能的重要因素之一。初始温度高，则搜索到全局最优解的可能性大，但因此要花费大量的计算时间；反之，则可节约计算时间，但全局搜索性能可能受到影响。实际应用过程中，初始温度一般需要依据实验结果进行若干次调整。

（2）温度衰减函数的选取。

      衰减函数用于控制温度的退火速度，一个常用的函数为：

 

式中a是一个非常接近于1的常数，t为降温的次数。

（3）马尔可夫链长度L的选取。

通常的原则是：在衰减参数T的衰减函数已选定的前提下，L的选取应遵循在控制参数的每一取值上都能恢复准平衡的原则。

3. TSP算法实现

3.1 TSP算法描述

   （1）TSP问题的解空间和初始解

    TSP的解空间S是遍访每个城市恰好一次的所有回路，是所有城市排列的集合。TSP问题的解空间S可表示为{1,2,…,n}的所有排列的集合，即S = {(c₁,c₂,…,c_n) | ((c₁,c₂,…,c_n)为{1,2,…,n}的排列）}，其中每一个排列S_i表示遍访n个城市的一个路径，c_i= j表示在第i次访问城市j。模拟退火算法的最优解与初始状态无关，故初始解为随机函数生成一个{1,2,…,n}的随机排列作为S₀。

（2）目标函数

    TSP问题的目标函数即为访问所有城市的路径总长度，也可称为代价函数：

                                              

    现在TSP问题的求解就是通过模拟退火算法求出目标函数C(c₁,c₂,…,c_n)的最小值，相应地，s^*= (c^*₁,c^*₂,…,c^*_n)即为TSP问题的最优解。

   （3）新解产生

新解的产生对问题的求解非常重要。新解可通过分别或者交替用以下2种方法产生：

①二变换法：任选序号u,v(设uvn)，交换u和v之间的访问顺序，若交换前的解为s_i= (c₁,c₂,…,c_u,…,c_v,…,c_n),交换后的路径为新路径，即：

s_i′= (c₁,…,c_u-1,c_v,c_v-1,…,c_u+1,c_u,c_v+1,…,c_n)

②三变换法：任选序号u,v和ω(u≤vω)，将u和v之间的路径插到ω之后访问，若交换前的解为s_i= (c₁,c₂,…,c_u,…,c_v,…,c_ω,…,c_n)，交换后的路径为的新路径为：

s_i′= (c₁,…,c_u-1,c_v+1,…,c_ω,c_u,…,c_v,c_ω+1,…,c_n)

（4）目标函数差

计算变换前的解和变换后目标函数的差值：

Δc′= c(s_i′)- c(s_i)

（5）Metropolis接受准则

根据目标函数的差值和概率exp(-ΔC′/T)接受s_i′作为新的当前解s_i，接受准则：

                            

3.2 TSP算法流程

    根据以上对TSP的算法描述，可以写出用模拟退火算法解TSP问题的流程图2 所示：

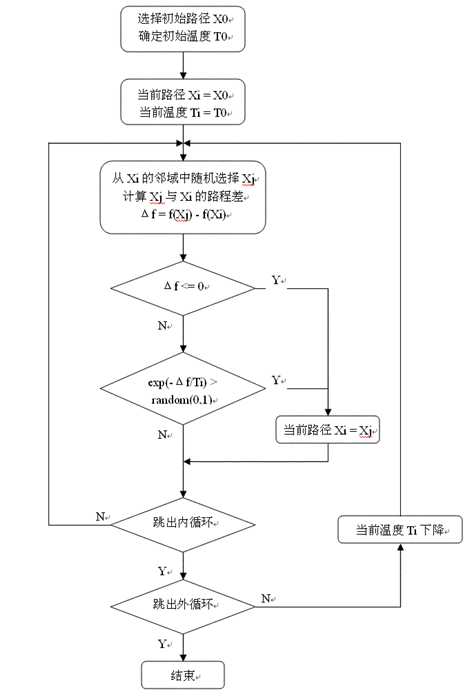
图 2  TSP的模拟退火流程

4.MATLAB实现

clear
clc

coordinates = load(‘data.txt‘); %加载数据

%设置参数
a = 0.99; % 温度衰减函数的参数
t0 = 97; tf = 3; t = t0;
Markov_length = 10000; % Markov链长度
amount = size(coordinates,1); % 城市的数目

% 通过向量化的方法计算距离矩阵
dist_matrix = zeros(amount, amount);
coor_x_tmp1 = coordinates(:,1) * ones(1,amount);
coor_x_tmp2 = coor_x_tmp1‘;
coor_y_tmp1 = coordinates(:,2) * ones(1,amount);
coor_y_tmp2 = coor_y_tmp1‘;
dist_matrix = sqrt((coor_x_tmp1-coor_x_tmp2).^2 + (coor_y_tmp1-coor_y_tmp2).^2); %存储各个城市之间距离的矩阵

sol_new = 1:amount; % 产生初始解
% sol_new是每次产生的新解；sol_current是当前解；sol_best是冷却中的最好解；
E_current = inf;E_best = inf; % E_current是当前解对应的回路距离；
% E_new是新解的回路距离；
% E_best是最优解的
sol_current = sol_new; sol_best = sol_new;
p = 1;

while t>=tf
for r=1:Markov_length % Markov链长度
% 产生随机扰动
if (rand < 0.5) % 随机决定是进行两交换还是三交换
% 两交换
ind1 = 0; ind2 = 0;
while (ind1 == ind2)
ind1 = ceil(rand.*amount);
ind2 = ceil(rand.*amount);
end
tmp1 = sol_new(ind1);
sol_new(ind1) = sol_new(ind2);
sol_new(ind2) = tmp1;
else
% 三交换
ind1 = 0; ind2 = 0; ind3 = 0;
while (ind1 == ind2) || (ind1 == ind3)|| (ind2 == ind3) || (abs(ind1-ind2) == 1)
ind1 = ceil(rand.*amount);
ind2 = ceil(rand.*amount);
ind3 = ceil(rand.*amount);
end
tmp1 = ind1;tmp2 = ind2;tmp3 = ind3;
% 确保ind1 < ind2 < ind3
if (ind1 < ind2) && (ind2 < ind3)
;
elseif (ind1 < ind3) && (ind3 < ind2)
ind2 = tmp3;ind3 = tmp2;
elseif (ind2 < ind1) && (ind1 < ind3)
ind1 = tmp2;ind2 = tmp1;
elseif (ind2 < ind3) && (ind3 < ind1)
ind1 = tmp2;ind2 = tmp3; ind3 = tmp1;
elseif (ind3 < ind1) && (ind1 < ind2)
ind1 = tmp3;ind2 = tmp1; ind3 = tmp2;
elseif (ind3 < ind2) && (ind2 < ind1)
ind1 = tmp3;ind2 = tmp2; ind3 = tmp1;
end

tmplist1 = sol_new((ind1+1):(ind2-1));
sol_new((ind1+1):(ind1+ind3-ind2+1)) = sol_new((ind2):(ind3));
sol_new((ind1+ind3-ind2+2):ind3) = tmplist1;
end

%检查是否满足约束

% 计算目标函数值（即内能）
E_new = 0;
for i = 1 : (amount-1)
E_new = E_new + dist_matrix(sol_new(i),sol_new(i+1));
end
% 再算上从最后一个城市到第一个城市的距离
E_new = E_new + dist_matrix(sol_new(amount),sol_new(1));

if E_new < E_current
E_current = E_new;
sol_current = sol_new;
if E_new < E_best
% 把冷却过程中最好的解保存下来
E_best = E_new;
sol_best = sol_new;
end
else
% 若新解的目标函数值小于当前解的，
% 则仅以一定概率接受新解
if rand < exp(-(E_new-E_current)./t)
E_current = E_new;
sol_current = sol_new;
else
sol_new = sol_current;
end
end
end
t=t.*a; % 控制参数t（温度）减少为原来的a倍
end

for i=1:length(coordinates)
plot(coordinates(i,1),coordinates(i,2),‘r*‘);
hold on;
end;

x=coordinates([sol_best sol_best(1)],1);
y=coordinates([sol_best sol_best(1)],2);
plot(x,y);
disp(‘最优解为：‘)
disp(sol_best)
disp(‘最短距离：‘)
disp(E_best)