平衡树
Posted pywbktda
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了平衡树相关的知识,希望对你有一定的参考价值。
例题1:[bzoj3224]&[luogu3369]普通平衡树(平衡树模板题)
题意:维护一个集合,支持:1.加入x;2.删除x;3.查询x排名;4.查询排名x的数;5.查询x前驱;6.查询x后继
0.3查询(有多少个数小于x)+1,4查询存在x个数小于等于它的最小数,5查询排名为(x排名-1)的数,6查询排名为((x+1)排名)的数
1.可以开一棵权值线段树/trie树(动态开点)来维护,维护区间和即可,比较简单

1 #include<bits/stdc++.h> 2 using namespace std; 3 #define mid (0LL+l+r>>1) 4 #define N 10000005 5 int V,n,r,p,x,f[N],ls[N],rs[N]; 6 void update(int &k,int l,int r,int x,int y) 7 if (!k)k=++V; 8 if (l==r) 9 f[k]+=y; 10 return; 11 12 if (x<=mid)update(ls[k],l,mid,x,y); 13 else update(rs[k],mid+1,r,x,y); 14 f[k]=f[ls[k]]+f[rs[k]]; 15 16 int query1(int k,int l,int r,int x,int y) 17 if ((l>y)||(x>r))return 0; 18 if ((x<=l)&&(r<=y))return f[k]; 19 return query1(ls[k],l,mid,x,y)+query1(rs[k],mid+1,r,x,y); 20 21 int query2(int k,int l,int r,int x) 22 if (l==r)return l; 23 if (f[ls[k]]>=x)return query2(ls[k],l,mid,x); 24 return query2(rs[k],mid+1,r,x-f[ls[k]]); 25 26 int main() 27 scanf("%d",&n); 28 while (n--) 29 scanf("%d%d",&p,&x); 30 if (p==1)update(r,-2e9,2e9,x,1); 31 if (p==2)update(r,-2e9,2e9,x,-1); 32 if (p==3)printf("%d\\n",query1(r,-2e9,2e9,1,x-1)+1); 33 if (p==4)printf("%d\\n",query2(r,-2e9,2e9,x)); 34 if (p==5)printf("%d\\n",query2(r,-2e9,2e9,query1(r,-2e9,2e9,1,x-1))); 35 if (p==6)printf("%d\\n",query2(r,-2e9,2e9,query1(r,-2e9,2e9,1,x)+1)); 36 37
BST:
1.BST(二叉查找树),它是二叉树且具有以下性质:1.左子树上所有结点小于根结点;2.右子树上所有结点大于根结点;3.左、右子树为BST
2.BST的节点:BST的每一个节点有节点大小、节点权值、子树大小、左右儿子5个属性需要维护
3.BST的删除:BST删除时需要将一个点不断旋转(见下)到其任意子树并递归下去,直到该节点只有0/1个儿子就用那个儿子替代他
4.发现这道题可以用BST来做这道题,但时间复杂度为o(树高),当插入数据单调而退化为链使得单次复杂度为o(n)
5.发现要维护这颗BST使其树高为o(log),即让其平衡,主要有旋转维护和非旋转维护两种方式
旋转:
1.旋转是维护BST平衡的重要操作,其主要作用是在保证BST性质的前提下将某一个儿子转到根节点
2.旋转示意图(又叫左旋和右旋):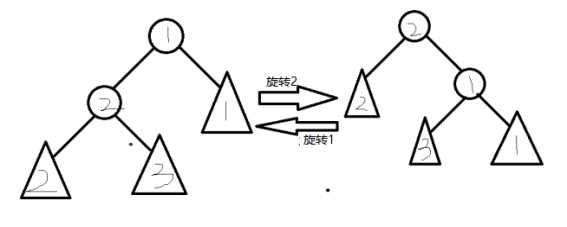
3.说明:容易发现这样的旋转是符合BST性质的,同时也改变了树的形状(具体方法详见代码)

1 void rotate(int &k,int u,int p)//将k的p儿子u旋转到k的位置 2 s(p)=ch[u][p^1];//s(p)表示k的p儿子 3 ch[u][p^1]=k;//以上两步即上图所示的旋转 4 up(k); 5 up(k=u);//重新计算k和u的子树大小,并让k(根)变为u 6
treap:
0.treap的基本思路是用随机的方式来保证树高
1.插入完一个点后,有50%的概率旋转他的每一个祖先(在搜索回去的时候旋转)
2.删除点时,选择左右儿子也用50%的概率选择

1 #include<bits/stdc++.h> 2 using namespace std; 3 #define N 100005 4 #define s(p) ch[k][p] 5 int V,r,n,p,x,sz[N],a[N],tot[N],ch[N][2]; 6 void New(int k,int x) 7 a[k]=x; 8 s(0)=s(1)=0; 9 sz[k]=tot[k]=1; 10 11 void up(int k) 12 sz[k]=sz[s(0)]+sz[s(1)]+tot[k]; 13 14 void rotate(int &k,int u,int p) 15 s(p)=ch[u][p^1]; 16 ch[u][p^1]=k; 17 up(k); 18 up(k=u); 19 20 void add(int &k,int x) 21 if (!k) 22 New(k=++V,x); 23 return; 24 25 sz[k]++; 26 if (a[k]==x) 27 tot[k]++; 28 return; 29 30 bool p=(a[k]<x); 31 add(s(p),x); 32 33 void del(int &k,int x) 34 if (!k)return; 35 sz[k]--; 36 if (a[k]==x) 37 if (--tot[k])return; 38 tot[k]++; 39 if (s(0)*s(1)==0)k=s(0)+s(1); 40 else 41 rotate(k,s(p),p); 42 del(k,x); 43 44 return; 45 46 del(s(a[k]<x),x); 47 48 int rank(int k,int x) 49 if (!k)return 1; 50 return rank(s(a[k]<x),x)+(a[k]<x)*(sz[s(0)]+tot[k]); 51 52 int kth(int k,int x) 53 if ((sz[s(0)]<x)&&(x<=sz[s(0)]+tot[k]))return a[k]; 54 return kth(s(sz[s(0)]<x),x-(sz[s(0)]<x)*(sz[s(0)]+tot[k])); 55 56 int main() 57 srand(time(0)); 58 scanf("%d",&n); 59 while (n--) 60 scanf("%d%d",&p,&x); 61 if (p==1)add(r,x); 62 if (p==2)del(r,x); 63 if (p==3)printf("%d\\n",rank(r,x)); 64 if (p==4)printf("%d\\n",kth(r,x)); 65 if (p==5)printf("%d\\n",kth(r,rank(r,x)-1)); 66 if (p==6)printf("%d\\n",kth(r,rank(r,x+1))); 67 68
3.然而这个东西随机次数较多,因此可以再维护一个堆性质的随机域,再用堆的方式up和down(详见代码)

1 #include<bits/stdc++.h> 2 using namespace std; 3 #define N 100005 4 #define s(p) ch[k][p] 5 int V,r,n,p,x,sz[N],a[N],tot[N],ch[N][2],ra[N]; 6 void New(int k,int x) 7 a[k]=x; 8 s(0)=s(1)=0; 9 sz[k]=tot[k]=1; 10 ra[k]=rand(); 11 12 void up(int k) 13 sz[k]=sz[s(0)]+sz[s(1)]+tot[k]; 14 15 void rotate(int &k,int u,int p) 16 s(p)=ch[u][p^1]; 17 ch[u][p^1]=k; 18 up(k); 19 up(k=u); 20 21 void add(int &k,int x) 22 if (!k) 23 New(k=++V,x); 24 return; 25 26 sz[k]++; 27 if (a[k]==x) 28 tot[k]++; 29 return; 30 31 bool p=(a[k]<x); 32 add(s(p),x); 33 if (ra[s(p)]<ra[k])rotate(k,s(p),p); 34 35 void del(int &k,int x) 36 if (!k)return; 37 sz[k]--; 38 if (a[k]==x) 39 if (--tot[k])return; 40 tot[k]++; 41 if (s(0)*s(1)==0)k=s(0)+s(1); 42 else 43 int p=(ra[s(0)]>ra[s(1)]); 44 rotate(k,s(p),p); 45 del(k,x); 46 47 return; 48 49 del(s(a[k]<x),x); 50 51 int rank(int k,int x) 52 if (!k)return 1; 53 return rank(s(a[k]<x),x)+(a[k]<x)*(sz[s(0)]+tot[k]); 54 55 int kth(int k,int x) 56 if ((sz[s(0)]<x)&&(x<=sz[s(0)]+tot[k]))return a[k]; 57 return kth(s(sz[s(0)]<x),x-(sz[s(0)]<x)*(sz[s(0)]+tot[k])); 58 59 int main() 60 srand(time(0)); 61 scanf("%d",&n); 62 while (n--) 63 scanf("%d%d",&p,&x); 64 if (p==1)add(r,x); 65 if (p==2)del(r,x); 66 if (p==3)printf("%d\\n",rank(r,x)); 67 if (p==4)printf("%d\\n",kth(r,x)); 68 if (p==5)printf("%d\\n",kth(r,rank(r,x)-1)); 69 if (p==6)printf("%d\\n",kth(r,rank(r,x+1))); 70 71
4.时间复杂度:以上两种方法复杂度都是$o(nlogn)$的(很显然,也不需要具体证明了要我也不会啊)
splay:
0.splay的基本性质是利用旋转的性质来保证时间复杂度(不保证树高)
1.旋转的性质:发现旋转的作用不仅仅是改变根,还可以用来改变树的结构
2.具体旋转方式:不断将被操作数/被询问数按以下方式旋转到根
(1)当这个节点已经是根节点的儿子,旋转到根后结束
(2)当这个节点自己和父亲是父亲和祖父的同一个儿子,先旋转父亲,再旋转自己(如下图)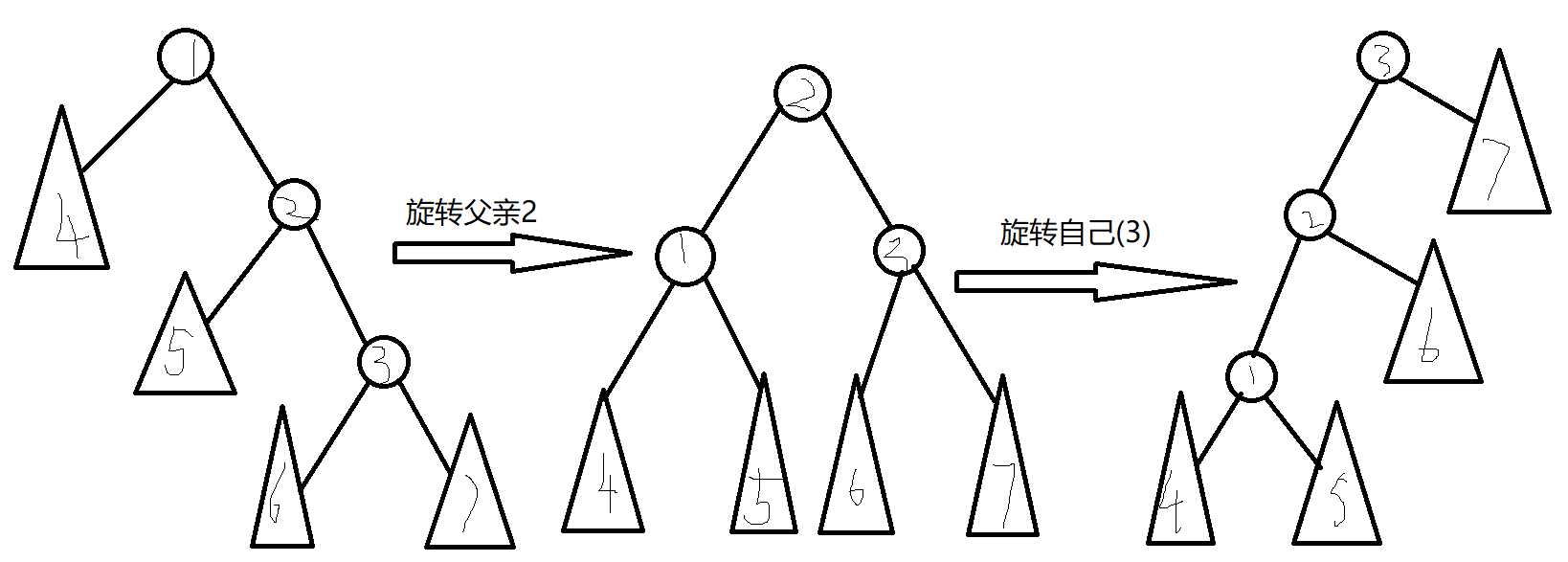
(3)当这个节点自己和父亲是父亲和祖父的不同儿子,旋转两次自己(如下图)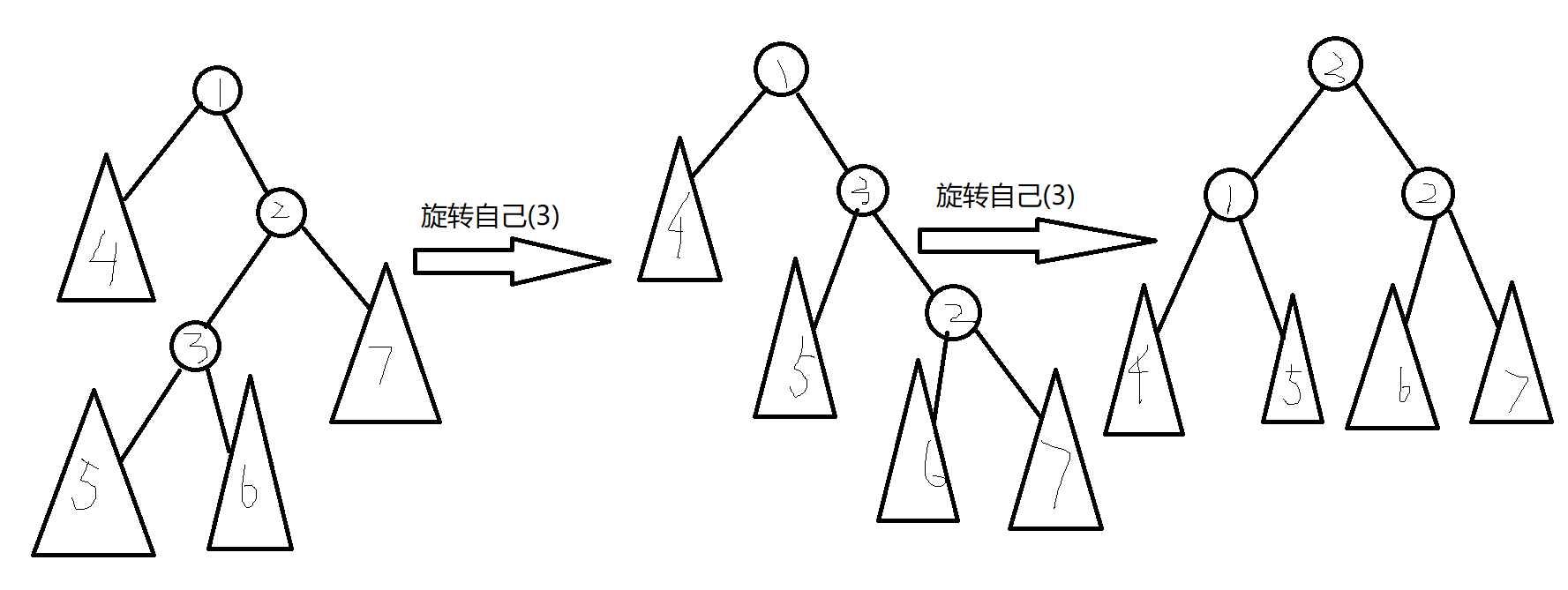
(4)为了维护这个操作,还需要记录每一个节点的父亲(详见代码splay函数)

1 bool pd(int k)//判断k是哪一个儿子 2 return (ch[fa[k]][1]==k); 3 4 void up(int k)//计算子树大小 5 sz[k]=sz[s(0)]+sz[s(1)]+tot[k]; 6 7 void rotate(int k)//旋转k 8 int x=fa[k],y=fa[x]; 9 bool p=pd(k); 10 ch[y][pd(x)]=k; 11 fa[k]=y; 12 ch[x][p]=ch[k][p^1]; 13 fa[ch[x][p]]=x; 14 ch[k][p^1]=x; 15 fa[x]=k;//旋转的过程(多修改一个f) 16 up(x); 17 up(k);//重新计算子树大小 18 19 void splay(int k,int x)//将k旋转到x的儿子 20 for(int i=fa[k];i!=x;rotate(k),i=fa[k]) 21 if (fa[i]!=x)rotate(pd(k)==pd(i)?i:k); 22 if (!x)r=k; 23
3.splay的删除:splay删除如果像treap那样就无法保证时间复杂度了,所以要借助splay操作
将该点的前驱旋转到根,该点的后继旋转到前驱的右儿子,只要删除就在后继的左儿子即可(注意特判最大和最小)

1 #include<bits/stdc++.h> 2 using namespace std; 3 #define N 100005 4 #define s(p) ch[k][p] 5 int V,r,n,p,x,sz[N],fa[N],a[N],tot[N],ch[N][2]; 6 void New(int k,int x,int f) 7 a[k]=x; 8 s(0)=s(1)=0; 9 fa[k]=f; 10 11 bool pd(int k) 12 return (ch[fa[k]][1]==k); 13 14 void up(int k) 15 sz[k]=sz[s(0)]+sz[s(1)]+tot[k]; 16 17 void rotate(int k) 18 int x=fa[k],y=fa[x]; 19 bool p=pd(k); 20 ch[y][pd(x)]=k; 21 fa[k]=y; 22 ch[x][p]=ch[k][p^1]; 23 fa[ch[x][p]]=x; 24 ch[k][p^1]=x; 25 fa[x]=k; 26 up(x); 27 up(k); 28 29 void splay(int k,int x) 30 for(int i=fa[k];i!=x;rotate(k),i=fa[k]) 31 if (fa[i]!=x)rotate(pd(k)==pd(i)?i:k); 32 if (!x)r=k; 33 34 void add(int &k,int x,int f) 35 if (!k)New(k=++V,x,f); 36 sz[k]++; 37 if (a[k]==x) 38 tot[k]++; 39 splay(k,0); 40 return; 41 42 bool p=(a[k]<x); 43 add(s(p),x,k); 44 45 int rank(int k,int x,int f) 46 if (!k) 47 splay(f,0); 48 return 1; 49 50 return (a[k]<x)*(sz[s(0)]+tot[k])+rank(s(a[k]<x),x,k); 51 52 int kth(int k,int x) 53 if ((sz[s(0)]<x)&&(x<=sz[s(0)]+tot[k])) 54 splay(k,0); 55 return k; 56 57 return kth(s(sz[s(0)]<x),x-(sz[s(0)]<x)*(sz[s(0)]+tot[k])); 58 59 int find(int x,int p) 60 if (!p)x=rank(r,x,0)-1; 61 else x=rank(r,x+1,0); 62 return kth(r,x); 63 64 void del(int x) 65 if ((rank(r,x,0)==1)||(rank(r,x+1,0)>sz[r])) 66 splay(find(x-1,1),0); 67 if (--tot[r]) 68 sz[r]--; 69 return; 70 71 r=ch[r][(ch[r][1]>0)]; 72 fa[r]=0; 73 return; 74 75 int k=find(x,1); 76 splay(find(x,0),0); 77 splay(k,r); 78 sz[r]--; 79 sz[k]--; 80 if (--tot[s(0)])sz[s(0)]--; 81 else fa[s(0)]=s(0)=0; 82 83 int main() 84 scanf("%d",&n); 85 while (n--) 86 scanf("%d%d",&p,&x); 87 if (p==1)add(r,x,0); 88 if (p==2)del(x); 89 if (p==3)printf("%d\\n",rank(r,x,0)); 90 if (p==4)printf("%d\\n",a[kth(r,x)]); 91 if (p==5)printf("%d\\n",a[find(x,0)]); 92 if (p==6)printf("%d\\n",a[find(x,1)]); 93 94
4.时间复杂度:当询问节点3很浅时,询问复杂度很低;当3比较深时,我们会将3及其子树内深度减小,所以最终复杂度为$o(nlogn)$
严谨的证明需要势能分析,详见:http://www.doc88.com/p-2763562792969.html
替罪羊树:
0.替罪羊树的基本思路是利用重构来保证树高
1.重构的操作:重构一棵子树,将这棵子树变成完全二叉树的BST(dfs一遍再建树)
2.重构的条件:当$max(sz[ls],sz[rs])>sz[k]*\\alpha$(sz表示子树大小,ls和rs表示k的左右儿子)将k的子树重构为完全二叉树
3.替罪羊树的删除:如果发现出现次数-1后变为0,直接对那个点打上一个删除标记即
4.alpha的选择:$\\alpha$的值域是[0.5,1),但经过理性分析,发现大约取[0,6,0.7](可以通过时间复杂度证明得出)

1 #include<bits/stdc++.h> 2 using namespace std; 3 #define N 100005 4 #define s(p) ch[k][p] 5 int V,r,n,p,x,sz[N],a[N],tot[N],v[N],ch[N][2]; 6 bool check(int k) 7 return max(sz[s(0)],sz[s(1)])*4>sz[k]*3; 8 9 void up(int k) 10 sz[k]=sz[s(0)]+sz[s(1)]+tot[k]; 11 12 void rotate(int &k,int u,int p) 13 s(p)=ch[u][p^1]; 14 ch[u][p^1]=k; 15 up(k); 16 up(k=u); 17 18 void add(int &k,int x) 19 if (!k)a[k=++V]=x; 20 sz[k]++; 21 if (a[k]==x) 22 tot[k]++; 23 return; 24 25 add(s(a[k]<x),x); 26 27 void del(int &k,int x) 28 if (!k)return; 29 sz[k]--; 30 if (a[k]==x) 31 tot[k]--; 32 return; 33 34 del(s(a[k]<x),x); 35 36 int rank(int k,int x) 37 if (!k)return 1; 38 return rank(s(a[k]<x),x)+(a[k]<x)*(sz[s(0)]+tot[k]); 39 40 int kth(int k,int x) 41 if ((sz[s(0)]<x)&&(x<=sz[s(0)]+tot[k]))return a[k]; 42 return kth(s(sz[s(0)]<x),x-(sz[s(0)]<x)*(sz[s(0)]+tot[k])); 43 44 void dfs(int k) 45 if (!k)return; 46 dfs(s(0)); 47 if (tot[k])v[++v[0]]=k; 48 dfs(s(1)); 49 50 void build(int &k,int l,int r) 51 if (l>r) 52 k=0; 53 return; 54 55 int mid=(l+r>>1); 56 k=v[mid]; 57 build(s(0),l,mid-1); 58 build(s(1),mid+1,r); 59 up(k); 60 61 void find(int &k,int x) 62 if (check(k)) 63 v[0]=0; 64 dfs(k); 65 build(k,1,v[0]); 66 return; 67 68 if (a[k]==x)return; 69 find(s(a[k]<x),x); 70 71 int main() 72 scanf("%d",&n); 73 while (n--) 74 scanf("%d%d",&p,&x); 75 if (p==1)add(r,x); 76 if (p==2)del(r,x); 77 if (p==3)printf("%d\\n",rank(r,x)); 78 if (p==4)printf("%d\\n",kth(r,x)); 79 if (p==5)printf("%d\\n",kth(r,rank(r,x)-1)); 80 if (p==6)printf("%d\\n",kth(r,rank(r,x+1))); 81 if (p<3)find(r,x); 82 83
5.时间复杂度:感觉网上没有很好的证明(大家都觉得显然啊),我就口胡一下吧
复杂度的证明同样需要用到势能分析(可以看https://wenku.baidu.com/view/2b93a9552af90242a995e513.html)
定义点k的势能$R(k)=|sz[ls]-rs[rs]|$,则$\\phi=\\sum R(k)/(2\\alpha-1)$
有一个比较重要的东西:发现n个点完全二叉树(最平衡的)$\\phi=0$
容易发现越平衡$\\phi$值越小,因此$\\phi(0)-\\phi(n)\\le 0$,接下来考虑$\\sum ai$
询问复杂度:每一个节点都会让子树大小至少乘上$1/\\alpha$,因此树高/复杂度为$o(log_1/\\alphan)$,无势能变化
插入/删除复杂度:同上,实际复杂度是$o(log_1/\\alphan)$,势能至多加上$o((log_1/\\alphan)/(2\\alpha-1))$(全部都是重儿子)
重构复杂度:假设对一棵大小为m的子树修改,实际复杂度为o(m),重构结束后$\\phi(i)=子树外$
最小化重构前的势能,即左右子树为完全二叉树,$\\phi(i-1)=o(m)+子树外$,最终$ai=o(m)+\\phi(i)-\\phi(i-1)=o(1)$
同时,发现时间复杂度为$o(nlog_1/\\alphan)/(2\\alpha-1)=o(nln(n)\\cdot(-ln(\\alpha)\\cdot (2\\alpha-1))$
前者只与n有关,考虑后者,即$f(\\alpha)=-ln(\\\\alpha)\\cdot (2\\alpha-1)$,$f‘(\\alpha)=ln(\\alpha)+2\\alpha-1=0$
解得$\\alpha=0.6$(左右),但实际一般取0.7也可以,还是要根据具体情况对拍调整一下
总结:
| 数据结构 | 实际时间 | 实际空间 | 实际代码 |
| 线段树 | 772ms | 118480kb | 1136B |
| treap | 632ms | 3636kb | 1531B |
| splay | 860ms | 3636kb | 1979B |
| 替罪羊树 | 512ms | 3636kb | 1615B |
当然,时间只能说明相对来说可能是这样的,毕竟有评测器、数据、人为等影响,只供参考
例题2:[bzoj3223]&[luogu3391]文艺平衡树(区间翻转模板题)
0.平衡树维护序列:类似于一种区间划分,不断选择一个点将区间分成两部分,同时保证了划分的次数不超过log(树高)
平衡树维护区间:可以用splay,类似于删除,将前驱提到根,后继放提到根右儿子,后继的左儿子的子树即该区间(特判首尾)
还可以用其他平衡树,但需要将区间划分为log段,因此区间要支持可合并,同线段树
1.翻转:显然暴力翻转复杂度太高(与暴力相同),可以用线段树的思想——打翻转的懒标记(注意下传)

1 #include<bits/stdc++.h> 2 using namespace std; 3 #define N 100005 4 #define s(p) ch[k][p] 5 int V,r,n,m,x,y,a[N],tag[N],sz[N],fa[N],ch[N][2]; 6 bool pd(int k) 7 return (ch[fa[k]][1]==k); 8 9 void New(int k,int x,int f) 10 a[k]=x; 11 tag[k]=s(0)=s(1)=0; 12 fa[k]=f; 13 sz[k]=1; 14 15 void rev(int k) 16 tag[k]^=1; 17 swap(s(0),s(1)); 18 19 void up(int k) 20 sz[k]=sz[s(0)]+sz[s(1)]+1; 21 22 void down(int k) 23 if (tag[k]) 24 tag[k]=0; 25 rev(s(0)); 26 rev(s(1)); 27 28 29 void rotate(int k) 30 int x=fa[k],y=fa[x]; 31 bool p=pd(k); 32 ch[y][pd(x)]=k; 33 fa[k]=y; 34 ch[x][p]=ch[k][p^1]; 35 fa[ch[x][p]]=x; 36 ch[k][p^1]=x; 37 fa[x]=k; 38 up(x); 39 up(k); 40 41 void splay(int k,int x) 42 down(k); 43 for(int i=fa[k];i!=x;rotate(k),i=fa[k]) 44 if (fa[i]!=x)rotate(pd(k)==pd(i)?i:k); 45 if (!x)r=k; 46 47 void add(int &k,int x,int f) 48 if (!k) 49 New(k=++V,x,f); 50 splay(k,0); 51 return; 52 53 add(s(a[k]<x),x,k); 54 55 int find(int k,int x) 56 if (sz[s(0)]+1==x)return k; 57 down(k); 58 return find(s(sz[s(0)]<x),x-(sz[s(0)]<x)*(sz[s(0)]+1)); 59 60 void dfs(int k) 61 if (!k)return; 62 down(k); 63 dfs(s(0)); 64 if ((1<k)&&(k<n+2))printf("%d ",k-1); 65 dfs(s(1)); 66 67 int main() 68 scanf("%d%d",&n,&m); 69 for(int i=1;i<=n+2;i++)add(r,i,0); 70 for(int i=1;i<=m;i++) 71 scanf("%d%d",&x,&y); 72 x=find(r,x); 73 splay(x,0); 74 y=find(r,y+2); 75 splay(y,r); 76 rev(ch[y][0]); 77 78 dfs(r); 79
例题3:[bzoj3065]带插入区间K小值(动态带插入区间第k小模板题,强制在线)
题意:询问给定序列动态(单点修改和单点插入)区间第k小
1.用平衡树,首先想到splay,但splay无法知道子树第k小(因为并不以权值为关键字)
2.发现只需要每一个节点开一棵权值线段树记录子树信息即可(即树套树),但平衡树就不能旋转了(改变量太大)
3.发现替罪羊树支持此操作,同时线段树是可合并的,所以划分成log个区间就可以了
4.替罪羊树重构时要使用线段树合并才可以,注意不能线段树合并共用节点且修改时不新建节点

1 #include<bits/stdc++.h> 2 using namespace std; 3 #define N 70005 4 #define s(p) ch[k][p] 5 #define mid (l+r>>1) 6 int r,n,m,p,x,y,z,ans,ro[N],a[N],v[N],v2[N],st[N*300],sz[N*300],ch[N*300][2]; 7 char s[11]; 8 void update(int &k,int l,int r,int x,int y) 9 if (!k)k=st[st[0]--]; 10 sz[k]+=y; 11 if (l==r)return; 12 if (x<=mid)update(s(0),l,mid,x,y); 13 else update(s(1),mid+1,r,x,y); 14 if (!sz[k]) 15 st[++st[0]]=k; 16 s(0)=s(1)=k=0; 17 18 19 int query(int l,int r,int x) 20 if (l==r)return l; 21 int s=0; 22 for(int i=1;i<=v[0];i++)s+=sz[ch[v[i]][0]]; 23 for(int i=1;i<=v2[0];i++)s+=(((l<=v2[i])&&(v2[i]<=mid))); 24 for(int i=1;i<=v[0];i++)v[i]=ch[v[i]][(s<x)]; 25 if (s>=x)query(l,mid,x); 26 else query(mid+1,r,x-s); 27 28 void merge(int &k,int k1,int k2) 29 if (k1+k2==0)return; 30 sz[k=st[st[0]--]]=sz[k1]+sz[k2]; 31 merge(s(0),ch[k1][0],ch[k2][0]); 32 merge(s(1),ch[k1][1],ch[k2][1]); 33 34 bool check(int k) 35 return max(sz[s(0)],sz[s(1)])*4>sz[k]*3; 36 37 void up(int k) 38 sz[k]=sz[s(0)]+sz[s(1)]+1; 39 merge(ro[k],ro[s(0)],ro[s(1)]); 40 update(ro[k],0,N,a[k],1); 41 42 void add(int &k,int x,int y) 43 if (!k) 44 sz[k=++n]=1; 45 update(ro[k],0,N,a[k]=y,1); 46 return; 47 48 sz[k]++; 49 update(ro[k],0,N,y,1); 50 bool p=(sz[s(0)]<x); 51 add(s(p),x-p*(sz[s(0)]+1),y); 52 53 int update(int k,int x,int y) 54 update(ro[k],0,N,y,1); 55 if (x==sz[s(0)]) 56 swap(a[k],y); 57 update(ro[k],0,N,y,-1); 58 return y; 59 60 bool p=(sz[s(0)]<x); 61 y=update(s(p),x-p*(sz[s(0)]+1),y); 62 update(ro[k],0,N,y,-1); 63 return y; 64 65 void find(int k,int x,int y) 66 if ((x==1)&&(y==sz[k])) 67 v[++v[0]]=ro[k]; 68 return; 69 70 if (x<=sz[s(0)])find(s(0),x,min(y,sz[s(0)])); 71 x-=sz[s(0)]+1; 72 y-=sz[s(0)]+1; 73 if (0<y)find(s(1),max(x,1),y); 74 if ((x<=0)&&(0<=y))v2[++v2[0]]=a[k]; 75 76 void dfs(int k) 77 if (!k)return; 78 dfs(s(0)); 79 v[++v[0]]=k; 80 dfs(s(1)); 81 82 void build(int &k,int l,int r) 83 if (l>r) 84 k=0; 85 return; 86 87 k=v[mid]; 88 build(s(0),l,mid-1); 89 build(s(1),mid+1,r); 90 up(k); 91 92 void find(int &k,int x) 93 if (check(k)) 94 v[0]=0; 95 dfs(k); 96 build(k,1,v[0]); 97 return; 98 99 if (x==sz[s(0)])return; 100 bool p=(sz[s(0)]<x); 101 find(s(p),x-p*(sz[s(0)]+1)); 102 103 int main() 104 scanf("%d",&n); 105 for(int i=N;i<=300*(N-5);i++)st[++st[0]]=i; 106 for(int i=1;i<=n;i++) 107 scanf("%d",&a[i]); 108 v[i]=i; 109 110 build(r,1,n); 111 scanf("%d",&m); 112 for(int i=1;i<=m;i++) 113 scanf("%s%d%d",s,&x,&y); 114 x^=ans; 115 y^=ans; 116 if (s[0]==‘M‘)update(r,x-1,y); 117 if (s[0]==‘I‘) 118 add(r,x-1,y); 119 find(r,x-1); 120 121 if (s[0]==‘Q‘) 122 scanf("%d",&z); 123 v[0]=v2[0]=0; 124 find(r,x,y); 125 printf("%d\\n",ans=query(0,N,z^ans)); 126 127 128
5.类似的题目还有[bzoj3600],也是要利用替罪羊树不需要旋转做
例题4:[luogu3835]可持久化平衡树(可持久化treap模板题)
题意:同例1,但询问为历史询问
0.很显然,发现这就是要可持久化一棵平衡树
1.可持久化的条件:1.时间复杂度非均摊;2.不能用旋转维护(单次修改量由1来保证)
2.发现上面三种平衡树并不能可持久化,于是fhq提出了一种基于treap思想的非旋treap
3.分裂——split(k,x,k1,k2):将k的小于x的数和剩下的分裂出来并存在k1和k2中,分为三种情况递归:
(1)子树为空,返回空树标记;
(2)全部在左区间,递归左区间确定根;
(3)包含了根/不全在左子树中,递归右区间确定根的右儿子。
4.合并——merge(k1,k2):将k1和k2合并并返回新的根(k1最大值小于k2最小值),分两种情况递归:
(1)k1的随机数<k2的随机数,将k2和k1的右子树合并并作为k1的右儿子;
(2)k1的随机数>k2的随机数,将k1和k2的左子树和并并作为k2的左儿子。
5.插入/删除:插入x,根据x分为两部分,并将x当作一棵树与另外两颗树合并即可;删除类似

1 #include<bits/stdc++.h> 2 using namespace std; 3 #define N 100005 4 #define s(p) ch[k][p] 5 int V,r,n,p,x,sz[N],a[N],ch[N][2],ra[N]; 6 int New(int x) 7 a[++V]=x; 8 sz[V]=1; 9 ra[V]=rand(); 10 return V; 11 12 void up(int k) 13 sz[k]=sz[s(0)]+sz[s(1)]+1; 14 15 void split(int k,int x,int &k1,int &k2) 16 if (!k) 17 k1=k2=0; 18 return; 19 20 if (x<a[k]) 21 k2=k; 22 split(s(0),x,k1,s(0)); 23 24 else 25 k1=k; 26 split(s(1),x,s(1),k2); 27 28 up(k); 29 30 int merge(int k1,int k2) 31 if (k1*k2==0)return k1+k2; 32 if (a[k1]>a[k2])swap(k1,k2); 33 int p=(ra[k1]<ra[k2]),k=k1*p+k2*(p^1); 34 s(p)=merge(s(p),k1+k2-k); 35 up(k); 36 return k; 37 38 void add(int x) 39 int a,b; 40 split(r,x,a,b); 41 r=merge(merge(a,New(x)),b); 42 43 void del(int x) 44 int a,b,c; 45 split(r,x-1,a,c); 46 split(c,x,b,c); 47 r=merge(merge(a,merge(ch[b][0],ch[b][1])),c); 48 49 int kth(int k,int x) 50 if (x==sz[s(0)]+1)return a[k]; 51 bool p=(sz[s(0)]<x); 52 return kth(s(p),x-p*(sz[s(0)]+1)); 53 54 int rank(int x) 55 int a,b,c; 56 split(r,x-1,a,b); 57 c=sz[a]+1; 58 r=merge(a,b); 59 return c; 60 61 int main() 62 srand(time(0)); 63 scanf("%d",&n); 64 while (n--) 65 scanf("%d%d",&p,&x); 66 if (p==1)add(x); 67 if (p==2)del(x); 68 if (p==3)printf("%d\\n",rank(x)); 69 if (p==4)printf("%d\\n",kth(r,x)); 70 if (p==5)printf("%d\\n",kth(r,rank(x)-1)); 71 if (p==6)printf("%d\\n",kth(r,rank(x+1))); 72 73
6.区间操作:类似于splay,直接用分别split掉左端点前和右端点后,然后提取出对应区间即可

1 #include<bits/stdc++.h> 2 using namespace std; 3 #define N 100005 4 #define s(p) ch[k][p] 5 int r,n,m,x,y,sz[N],ra[N],laz[N],ch[N][2]; 6 void update(int k) 7 swap(s(0),s(1)); 8 laz[k]^=1; 9 10 void down(int k) 11 if (laz[k]) 12 update(s(0)); 13 update(s(1)); 14 laz[k]=0; 15 16 17 void up(int k) 18 sz[k]=sz[s(0)]+sz[s(1)]+1; 19 20 void split(int k,int x,int &k1,int &k2) 21 if (!k) 22 k1=k2=0; 23 return; 24 25 down(k); 26 if (x<=sz[s(0)]) 27 k2=k; 28 split(s(0),x,k1,s(0)); 29 30 else 31 k1=k; 32 split(s(1),x-sz[s(0)]-1,s(1),k2); 33 34 up(k); 35 36 int merge(int k1,int k2) 37 if (k1*k2==0)return k1+k2; 38 int p=(ra[k1]<ra[k2]),k=k1*p+k2*(p^1); 39 down(k); 40 if (p)s(1)=merge(s(1),k2); 41 else s(0)=merge(k1,s(0)); 42 up(k); 43 return k; 44 45 void dfs(int k) 46 if (!k)return; 47 down(k); 48 dfs(s(0)); 49 printf("%d ",k); 50 dfs(s(1)); 51 52 int main() 53 srand(time(0)); 54 scanf("%d%d",&n,&m); 55 for(int i=1;i<=n;i++) 56 ra[i]=rand(); 57 sz[i]=1; 58 r=merge(r,i); 59 60 for(int i=1;i<=m;i++) 61 scanf("%d%d",&x,&y); 62 int a,b,c; 63 split(r,x-1,a,b); 64 split(b,y-x+1,b,c); 65 update(b); 66 r=merge(merge(a,b),c); 67 68 dfs(r); 69
7.可持久化:分裂与合并都在原来的基础上进行即可(详见代码)

1 #include<bits/stdc++.h> 2 using namespace std; 3 #define N 500005 4 #define s(p) ch[k][p] 5 int V,n,t,p,x,r[N],a[N*50],ra[N*50],sz[N*50],ch[N*50][2]; 6 int New(int x) 7 a[++V]=x; 8 sz[V]=1; 9 ra[V]=rand(); 10 return V; 11 12 int copy(int k) 13 a[++V]=a[k]; 14 sz[V]=sz[k]; 15 ra[V]=ra[k]; 16 memcpy(ch[V],ch[k],8); 17 return V; 18 19 void up(int k) 20 sz[k]=sz[s(0)]+sz[s(1)]+1; 21 22 void split(int k,int x,int &k1,int &k2) 23 if (!k) 24 k1=k2=0; 25 return; 26 27 if (x<a[k]) 28 k2=copy(k); 29 split(ch[k2][0],x,k1,ch[k2][0]); 30 up(k2); 31 32 else 33 k1=copy(k); 34 split(ch[k1][1],x,ch[k1][1],k2); 35 up(k1); 36 37 38 int merge(int k1,int k2) 39 if (k1*k2==0)return k1+k2; 40 int k; 41 if (ra[k1]<ra[k2]) 42 k=copy(k1); 43 s(1)=merge(s(1),k2); 44 45 else 46 k=copy(k2); 47 s(0)=merge(k1,s(0)); 48 49 up(k); 50 return k; 51 52 void add(int &r,int x) 53 int a,b; 54 split(r,x,a,b); 55 r=merge(merge(a,New(x)),b); 56 57 void del(int &r,int x) 58 int a,b,c; 59 split(r,x-1,a,c); 60 split(c,x,b,c); 61 r=merge(merge(a,merge(ch[b][0],ch[b][1])),c); 62 63 int kth(int k,int x) 64 if (x==sz[s(0)]+1)return a[k]; 65 bool p=(sz[s(0)]<x); 66 return kth(s(p),x-p*(sz[s(0)]+1)); 67 68 int rank(int &r,int x) 69 int a,b,c; 70 split(r,x-1,a,b); 71 c=sz[a]+1; 72 r=merge(a,b); 73 return c; 74 75 int main() 76 srand(time(0)); 77 scanf("%d",&n); 78 for(int i=1;i<=n;i++) 79 scanf("%d%d%d",&t,&p,&x); 80 r[i]=r[t]; 81 if (p==1)add(r[i],x); 82 if (p==2)del(r[i],x); 83 if (p==3)printf("%d\\n",rank(r[i],x)); 84 if (p==4)printf("%d\\n",kth(r[i],x)); 85 if (p==5)printf("%d\\n",kth(r[i],rank(r[i],x)-1)); 86 if (p==6)printf("%d\\n",kth(r[i],rank(r[i],x+1))); 87 88
8.类似的还有[luogu5055],只需要再维护一个子树和即可,注意标记的处理
总结:
各种平衡树所能处理的问题——
1.treap:码量较低,只能处理基本的平衡树问题
2.splay:码量较大,主要用于:1.不支持合并的区间问题;2.降低算法理论复杂度
3.替罪羊树:码量中等,主要用于单点信息量较大的问题(包括树套树)
4.非旋treap:码量较低,基本支持一切平衡树的问题,同时还支持可持久化
以上是关于平衡树的主要内容,如果未能解决你的问题,请参考以下文章
解密树的平衡:二分搜索树 → AVL自平衡树 → 左倾红黑树
解密树的平衡:二分搜索树 → AVL自平衡树 → 左倾红黑树
