经典模型——并查集解决区间/树链染色问题

Posted 2022-08-08 i-cookie

蒟蒻的第一篇blog

---

模型背景：

已知一个长度为n的序列，开始时序列的每一个元素都没有颜色（0），现进行m次操作，第i次操作将一段区间[l,r]中还未被染色的点(即a[i]=0的点)染成颜色i.问m次操作后这个区间长什么样子,并将它输出来.

数据规模约定:对于100%的数据,n,m<=10^6

问题解决

1. 我会nm暴力!

对于每一个操作i,暴力扫描[l,r],染色,最后输出.

※期望得分:10.

1. 并查集!没想到吧

用并查集来维护从节点i往后的区间[i,n]中第一个0出现的位置,也就是i之后第一个还未被染色的点的位置.

这是怎么做到的呢?

一开始每个节点的father显然指向自己(所有点都没染色).如果这个点被染了色,就将它与它的右边第一个点union起来,即father[i] = father[i+1].
比如:

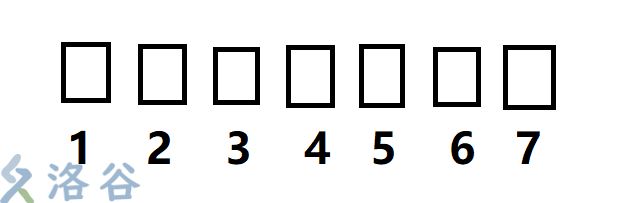
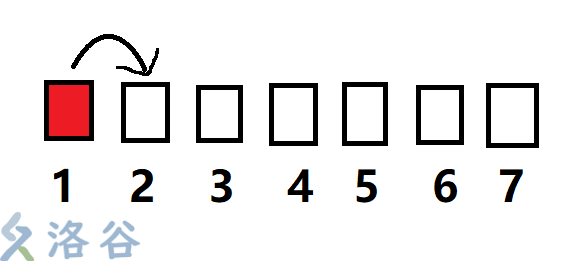
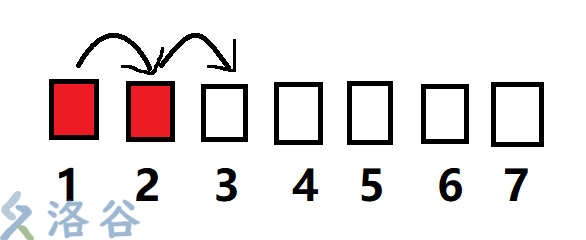
经过几次之后的染色以及一番奇妙的路径压缩,序列将形成类似这种样子

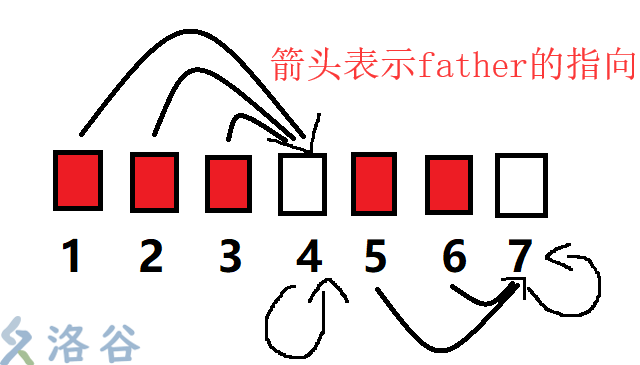
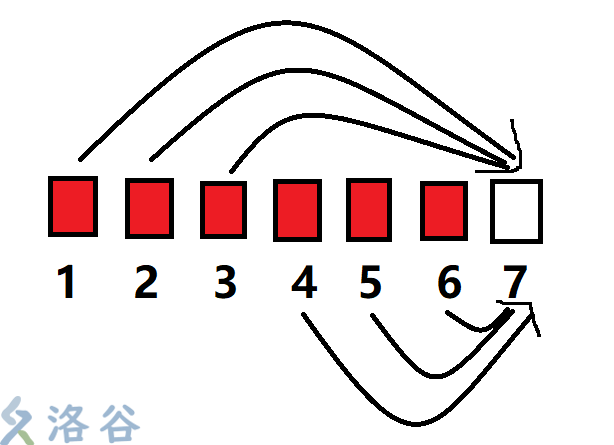
这样,不就给下一次的操作省时间了吗,不就能一跳就跳到下一个0的地方染色了吗(欣喜)

核心代码:

int findfather(int x) //找下一个为0的点,顺便路径压缩
    if (father[x] != x)
        father[x] = findfather(father[x]);
    return father[x];


inline int combine(int x, int y) //union
    int fx = findfather(x);
    int fy = findfather(y);
    if (fx != fy)
        father[fx] = fy;
    return;


int main() 
    /*读入等操作略*/
    for (int i = 1; i <= m; ++i) //染色
        for (int j = findfather(l); j <= r; j = findfather(j)) 
            color[j] = i;
        
    
    /*输出操作略*/

怎么样,是不是很好懂呢?

然而,

如果是要对树上的链进行染色的话,又该如何做呢?

1. 这不就是树链剖分吗,上树剖啊

嗯,看起来就好像 【模板】树链剖分 的简化版.但是请回头看一眼数据范围.嗯,由于树剖的时间瓶颈在于线段树,树剖显然无法解决10^6级别的数据

期望得分:80.

1. 并查集!没想到吧

对于树上的一条链(u,v),除了通过树链剖分来处理以外,我们还可以通过将这条链分割成(u,LCA),(LCA,v)来解决.类比之前对于一段序列的做法,我们可以改进出这样的做法:

问题解决

在上一个模型中,我们发现了一种从一个点直接跳到下一个未染色的点的方法,那就是用并查集+路径压缩不断往右指.这个问题也一样.当一个点被染色时,我们可以将它的并查集数组指向它的父节点(即father[i]=fa[i],father[i]是i节点的并查集数组,fa[i]是它在题目中树上的父亲节点).

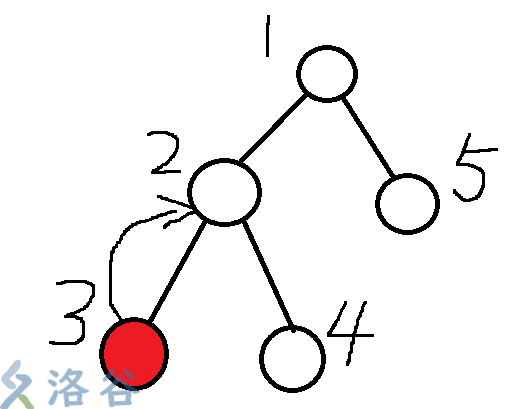
接下来就可以类比之前的问题了.若要给(3,5)染色,就由深度大的开始往上跳,不过这个跳是findfather那种跳(雾).

问题解决了吗?

实际跳的时候会发现,它可能会跳到LCA以上的地方!

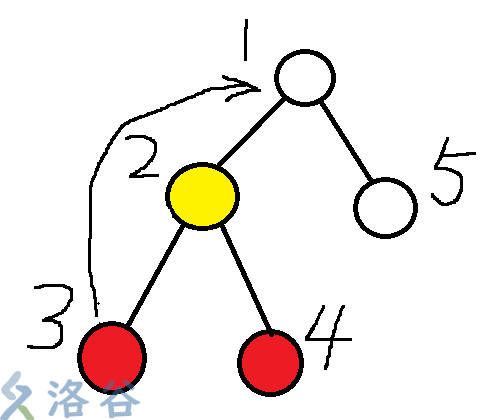
你会发现,如果2之前被染过色,那么路径压缩的时候会直接将3的father连到1上!

因此需要加一些特判,不让它往高处跳.

还有不懂的地方的话,就来看代码吧XD:

/*我个人比较喜欢借助树链剖分来求LCA,也可以采用其他方法*/

int findfather(int x) //略

inline void combine(int x, int y) //略

inline int LCA(int x, int y) //略

inline void paint(int x, int y, int c) 
    int lca = LCA(x, y);
    while (x != y) 
        if (dep[x] < dep[y])
            swap(x, y);//每次让深度大的向上跳
        x = dep[findfather(x)] < dep[lca] ? lca : father[x];//特判,阻止X往上方跳
        col[x] = c, combine(x, fa[x]);
    
    return;

这样问题就解决了!

欢迎指正和批评!