蒟蒻林荫小复习——KMP算法

Posted 2022-07-10 xlinyin

KMP算法，顾名思义，就是（看毛片）单个字符串匹配算法

KMP算法是一种改进的字符串匹配算法，由D.E.Knuth，J.H.Morris和V.R.Pratt提出的，因此人们称它为克努特—莫里斯—普拉特操作（简称KMP算法）。KMP算法的核心是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是通过一个next()函数实现，函数本身包含了模式串的局部匹配信息。KMP算法的时间复杂度O(m+n)。

这玩意能干啥？

1. 单对单的字符串匹配
2. 与可爱的TRIE结合后变成AC自动机

这东西啥原理？

举个栗子：假设原串：000000000001，模式串00001

那如果按照暴力的话，每次失去同步失配，就让在原串的起点++，模式串从头开始，对于上面的例子那铁定是不优的。

（每次匹配到模式串第5位就要从原串的第一位开始匹配，共计5*7+5次匹配。复杂度接近N*M）

分析上面的暴力，我们可以发现暴力劣在没有能利用局部匹配信息。比如匹配到第五位失配了，那么对于下面的几个原串的元素是否可以从第五位开始匹配？这样的话，匹配次数就是5+1*10+1=16.

OK,开始进入正题原来上面全是废话啊

KMP算法的基本原理就是：永不后退格拉尼原串P指针i，当模式串S指针j失配，即P[i+1]!=S[j+1],将j先移到1，然后尽可能的向右移动，

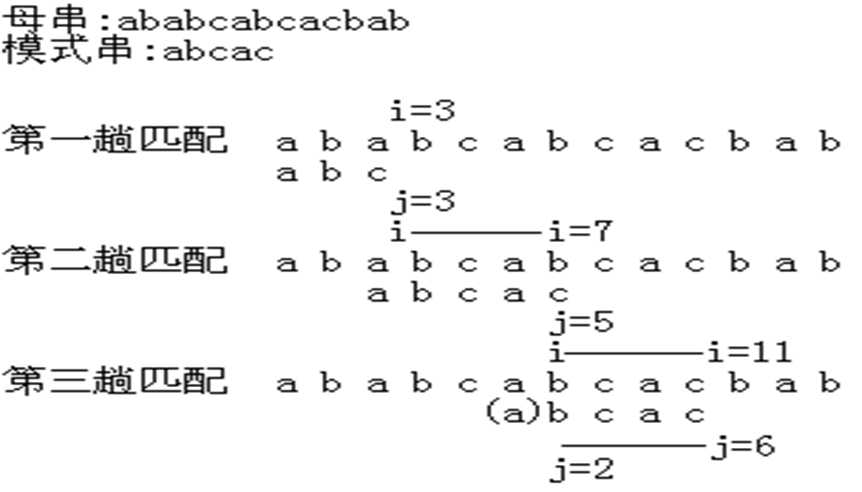
用指针i和j表示P[i-j+1]到P[i]与S[1]到S[j]完全相等，当P[i]==S[j]时，各自++，否则，i不变，j=next[j]（除非j已经等于-1，这个时候代表模式串无法找到一个位置使得P[i]==S[j],那么只能让i++，j++从模式串第一位开始匹配）,next数组中即储存j可以向右移动的最大位置。

那么显然可见这个时候j=next[j]后一定能保证P[i-1]==S[j-1]且前面j-1个元素也相等，这个时候我们需要比较的就是S[j]与P[i],如果相等，就继续下去，否则j=next[j];

next数组的实际意义则是在j位置失配时，在j之前离j最近的元素，并且这个元素next[j]还保证从j开始向前数X个元素与从next[j]向前数min(next[j],X)个元素完全相同.说白了就是j以前的串所有的性质在next[j]长度耗尽之前都能满足。

感性理解一下吧

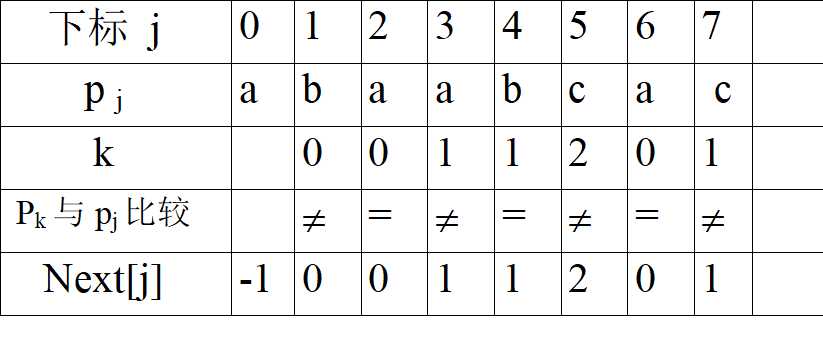
对于P=abaabcac而言

 那么求next的代码自己思考吧

makeNext(string p, int *next)
/* 变量next是数组next的第一个元素next[0]的地址 */
        int j, k;
    k= -1;     j=0;   next[0]= -1;    /* 初始化 */
    while (j<p.length()-1)    /* 计算next[j+1] */
               
               if(k<0 || p[j]= =p[k]) 
                     next[++j]= ++k;
             else  
                    k=next[k];        
           
       

Next的计算

 

这样的话，整个KMP算法最难的一部分就完成了，下面就是KMP的主体部分了

1. 比较当前的P[i]和S[j],相等去2，否则去3
2. i++，j++，如果j==S.size();这个时候就已经找到啦。就是P[i-j+1]到P[i]。
3. j=next[j]。
4. 如果这个时候j>P.size()退出，你这辈子都找不到啦hhhh
5. 如果这个时候的j==-1，那么进入2，否则进入1。

int index(string p,string s, int *next)
      int i,j;
      int M=p.length(),  N=p.length();
     i=0;  j=0;    /*初始化*/
      while (i<N && j<M)    /*反复比较*/
      if (j<0 || s[i]= =p[j])
           i++; j++; 
        else  j=next[j] ;
    if (j>=M)
           return( i - M + 1);    /*匹配成功*/
    else
              return( -1 );    /*匹配失败*/
  

KMP

完结撒花！！！！！