jzoj6276. noip提高组模拟1树

Posted 2022-06-21 rainbowcrown

Time Limits: 1000 ms

Memory Limits: 524288 KB

Description

有一棵n个节点的无根树，给出其中的m对点对<x,y>。问有多少条树上的简单路径<u,v>满足该路径上不存在任何一对给出的点对<x,y>。
这里我们认为路径<u,v>和<v,u>是相同的。并且对于题目中给出的点对<x,y>满足x!=y，对于你要计数的路径<u,v>满足u!=v（即单点不算答案）。

Input

第一行两个正整数n,m。
接下来n-1行每行两个正整数u,v描述树上的一条边。
接下来m行每行两个正整数x,y描述一对给出的点对。
（注意，这里我们不保证同样的点对<x,y>不会重复出现）

Output

一行一个整数，表示满足要求的树上简单路径的条数。

Sample Input

8 3
1 2
1 3
4 8
2 4
2 5
3 6
3 7
2 3
4 8
6 7

Sample Output

11

Data Constraint

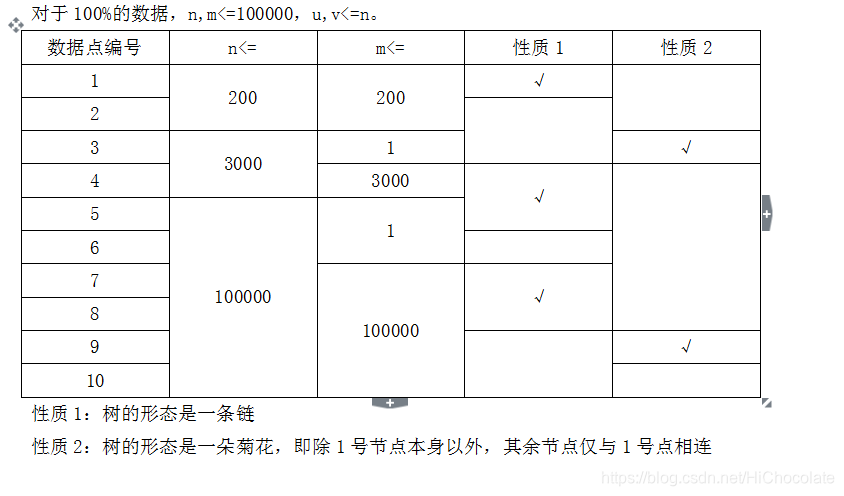
Hint

满足条件的路径为<1,2>，<1,3>，<1,4>，<1,5>，<1,6>，<1,7>，<2,4>，<2,5>，< 3,6>，< 3,7>，<4,5>。

赛时

一看到这么多的√，心想——一定可以水到巨多的分数。
看到m=1，不是送的吗？直接拿总答案减去不合法的即可。
看到菊花图，不是送的吗？如果不合法的限制一个是叶子，一个是根，则把叶子删掉。
剩下的-1即可。
看到链的情况，发现不会。
然后又发现n和m那么小，于是稳拿70.
最后发现，我?把调试程序交上去了！！！（调试输出的东西没删）
然后还没发现到限制重复。
10分妙啊♂

题解

部分分上面说过了，除了链的情况。
我们发现，对于链，直观的想法——设限制为x，y，y是x的祖宗。
那么y的祖先与x的儿子两两匹配都是不行的（显然）。
那么我们弄出一个二维平面，x轴表示从第i个点出发，y轴表示抵达第j个点。
这样就变成了在二维平面内有很多矩形，这些矩形内的点不能选。
这玩意不是扫描线吗？

即可解决，拿到90分的好成绩。

等等，既然我们想到这里了，100分不就很显然了吗？
我们对于数弄出dfn序，那么我们可以很轻松地处理出每个点对应的子树。
在二维平面内搞搞即可。
但是！如果y是x祖宗这类情况怎么办？
很简单，求出一个y到x简单路径中距离y最近的点z。
然后由于是dfn序，那么对于y以外的点就是除了z子树范围的其他点。
分成两个区间即可。

标程

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

struct qy

    int bz,sum;
;
struct kk

    int x,l,r,gg;
;

long long n,m,i,j,k,x,y,ans,t,l1,r1,l2,r2,sum,bz;
long long l[200005],next[200005],last[200005],tot;
long long depth[200005],dfn[200005],size[200005],fa[200005][18];
kk list[800005];
qy tree[800005];

void buildtree(long long x,long long faa)

    size[x]=1;
    dfn[x]=++sum;
    for (int i=1;i<=17;i++)
    
        fa[x][i]=fa[fa[x][i-1]][i-1];
    
    for (long long i=last[x];i>=1;i=next[i])
    
        if (l[i]!=faa)
        
            depth[l[i]]=depth[x]+1;
            fa[l[i]][0]=x;
            buildtree(l[i],x);
            size[x]+=size[l[i]];
        
    


void insert(long long x,long long y)

    l[++tot]=y;
    next[tot]=last[x];
    last[x]=tot;


void add(long long l1,long long r1,long long l2,long long r2)

    tot++;
    list[tot].l=l2;list[tot].r=r2;
    list[tot].x=l1;list[tot].gg=1;
    tot++;
    list[tot].l=l2;list[tot].r=r2;
    list[tot].x=r1+1;list[tot].gg=-1;
    
    tot++;
    list[tot].l=l1;list[tot].r=r1;
    list[tot].x=l2;list[tot].gg=1;
    tot++;
    list[tot].l=l1;list[tot].r=r1;
    list[tot].x=r2+1;list[tot].gg=-1;


int comp(kk a,kk b)

    return a.x<b.x;


int jump(int x,int steps)

    int y=x;
    for (int i=17;i>=0;i--)
    
        if (depth[x]-depth[fa[y][i]]<=steps)
        
            y=fa[y][i];
        
    
    return y;


void build(int k,int l,int r)

    tree[k].sum=r-l+1;
    tree[k].bz=0;
    if (l!=r)
    
        int mid=(l+r)/2;
        build(k*2,l,mid);
        build(k*2+1,mid+1,r);
    


void modify(int k,int l,int r,int x,int y,int z)

    if ((l<=y)&&(r>=x))
    
        if ((l>=x)&&(r<=y))
        
            tree[k].bz+=z;
            if (tree[k].bz==0)
            
                if (l!=r)
                tree[k].sum=tree[k*2].sum+tree[k*2+1].sum;
                else
                tree[k].sum=1;
            
            else
            tree[k].sum=0;
            return;
        
        int mid=(l+r)/2;
        modify(k*2,l,mid,x,y,z);
        modify(k*2+1,mid+1,r,x,y,z);
        if (tree[k].bz==0)
        tree[k].sum=tree[k*2].sum+tree[k*2+1].sum;
        else
        tree[k].sum=0;
    


int main()

    freopen("tree.in","r",stdin);
    freopen("tree.out","w",stdout);
    scanf("%lld%lld",&n,&m);
    for (i=1;i<=n-1;i++)
    
        scanf("%lld%lld",&x,&y);
        insert(x,y);
        insert(y,x);
    
    depth[1]=1;
    buildtree(1,0);
    tot=0;
    for (i=1;i<=m;i++)
    
        scanf("%lld%lld",&x,&y);
        if (depth[x]<depth[y]) swap(x,y);
        if ((depth[x]==depth[y])||(jump(x,depth[x]-depth[y])!=y))
        
            l1=dfn[x];
            r1=dfn[x]+size[x]-1;
            l2=dfn[y];
            r2=dfn[y]+size[y]-1;
            add(l1,r1,l2,r2);
        
        else
        
            t=jump(x,depth[x]-depth[y]-1);
            l1=dfn[x];
            r1=dfn[x]+size[x]-1;
            l2=1;
            r2=dfn[t]-1;
            add(l1,r1,l2,r2);
            l2=dfn[t]+size[t];
            r2=n;
            add(l1,r1,l2,r2);
        
    
    sort(list+1,list+1+tot,comp);
    build(1,1,n);
    bz=0;
    for (i=1;i<=n;i++)
    
        while ((bz+1<=tot)&&(list[bz+1].x<=i))
        
            bz++;
            modify(1,1,n,list[bz].l,list[bz].r,list[bz].gg);
        
        ans=ans+tree[1].sum;
    
    printf("%lld",(ans-n)/2);