斐波那契数列的三种时间复杂度

Posted 2022-05-27 zlshtml

/*前边两个为一种做法*/

/*后边有另外的做法（差分方程以及利用矩阵去做）*/

 

 

//***************************************************//***************************************************//***************************************************

第一种做法

这是2018王道数据结构考研复习指导的第一章思维拓展的题目。

关于斐波那契数列的简介：

　　斐波那契数列，又称黄金分割数列，指的是这样一个数列：0、1、1、2、3、5、8、13、21、34、……在数学上，斐波纳契数列以如下被以递归的方法定义：F（0）=0，F（1）=1，F（n）=F(n-1)+F(n-2)（n≥2，n∈N*）在现代物理、准晶体结构、化学等领域，斐波纳契数列都有直接的应用，为此，美国数学会从1963起出版了以《斐波纳契数列季刊》为名的一份数学杂志，用于专门刊载这方面的研究成果。

 

具体题目：

求解斐波那契数列的F(n)有两种常用算法：递归算法和非递归算法。试分析两种算法的时间复杂度。

1.递归算法

 1 #include<iostream>
 2 using namespace std;
 3 
 4 long Fibonacci(int n) 
 5     if (n == 0)
 6         return 0;
 7     else if (n == 1)
 8         return 1;
 9     else
10         return Fibonacci(n - 1) + Fibonacci(n-2);
11 
12 
13 int main() 
14     cout << "Enter an integer number:" << endl;
15     int N;
16     cin >> N;
17     cout << Fibonacci(N) << endl;
18     system("pause");
19     return 0;
20 

时间复杂度分析：

　　求解F(n),必须先计算F(n-1)和F(n-2),计算F(n-1)和F(n-2)，又必须先计算F(n-3)和F(n-4)。。。。。。以此类推，直至必须先计算F(1)和F(0),然后逆推得到F(n-1)和F(n-2)的结果，从而得到F(n)要计算很多重复的值，在时间上造成了很大的浪费，算法的时间复杂度随着N的增大呈现指数增长，时间的复杂度为O(2^n)，即2的n次方

2.非递归算法

 1 #include<iostream>
 2 using namespace std;
 3 
 4 long Fibonacci(int n) 
 5     if (n <= 2)
 6         return 1;
 7     else 
 8         long num1 = 1;
 9         long num2 = 1;
10         for (int i = 2;i < n - 1;i++) 
11             num2 = num1 + num2;
12             num1 = num2 - num1;
13         
14         return num1 + num2;
15     
16 
17 
18 int main() 
19     cout << "Enter an integer number:" << endl;
20     int N;
21     cin >> N;
22     cout << Fibonacci(N) << endl;
23     system("pause");
24     return 0;
25 

时间复杂度分析：

　　　从n(>2)开始计算，用F(n-1)和F(n-2)两个数相加求出结果，这样就避免了大量的重复计算，它的效率比递归算法快得多，算法的时间复杂度与n成正比，即算法的时间复杂度为O(n).

 

 

 

/**************************************************************************************************************************************************************************************************************/

第二种做法。

应用网址：

https://blog.csdn.net/beautyofmath/article/details/48184331

斐波那契数列: f(n)=f(n-1)+f(n-2); n>=2
f(0)=0; f(1)=1;
即有名的兔子繁衍问题。
斐波那契数列共有三种解法，因而写这篇文章总结一下。
1. 递归求解
递归求解比较简单，是大家常见的一种解法。

 1 int fibonacci(int n)
 2 
 3     cout<<"calculating "<<n<<endl;
 4     if (n<=0) 
 5         return  0;
 6     
 7     if (n==1) 
 8         return 1;
 9     
10     return fb(n-1)+fb(n-2);
11 

关于这种解法，不再赘述，下面主要说下时间复杂度分析。
设f(n)为参数为n时的时间复杂度，很明显：f(n)=f(n-1)+f(n-2)
这就转化为了数学上的二阶常系数差分方程，并且为其次方程。
即转化为了求f(n)的值，f(n)=f(n-1)+f(n-2)且f(0)=0; f(1)=1;
特征方程为：x^2-x-1=0
得 x=(1±√5)/2
因而f(n)的通解为:

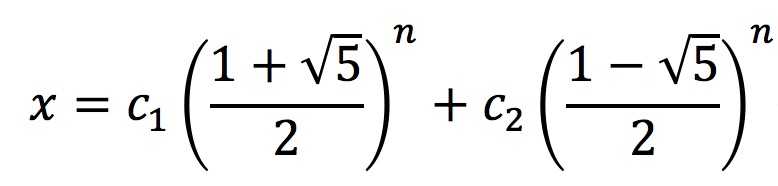
由f(0)=0; f(1)=1可解得c_1，c_2
最终可得，时间复杂度为：

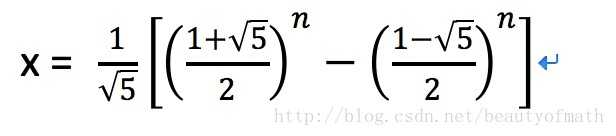
第一种解法比较简单，但是多个元素重复计算，因而时间复杂度较高，为了避免重复计算，可进行循环计算减少时间复杂度

 1 int Fibonacci(int n) 
 2 if (n<=0) 
 3 return 0;
 4 
 5 if (n==1) 
 6 return 1;
 7 
 8 int min=0;
 9 int max=1;
10 int i=2;
11 int result=0;
12 while (i<=n) 
13 result=min+max;
14 min=max;
15 max=result;
16 ++i;
17 
return result;

 第二种算法时间复杂度为O(n) 
3. 还有一种时间复杂度更低的算法。 
根据上面的递归公式，我们可以得到 

 

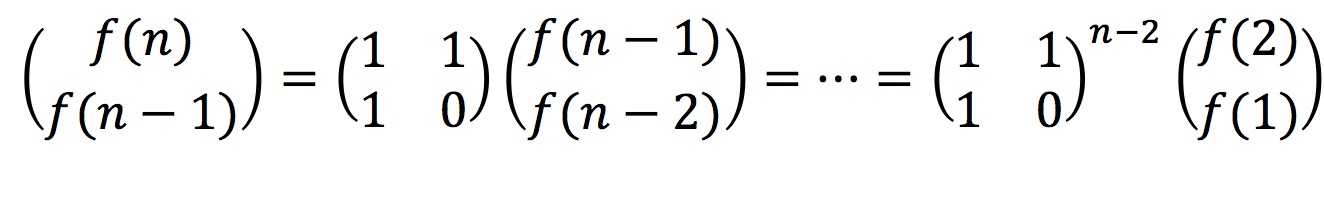
因而计算f(n)就简化为了计算矩阵的(n-2)次方，而计算矩阵的(n-2)次方，我们又可以进行分解，即计算矩阵(n-2)/2次方的平方，逐步分解下去，由于折半计算矩阵次方，因而时间复杂度为O(log n) 
具体代码实现如下：

 

 1 //
 2 //  main.cpp
 3 //  fibonaccimatrix
 4 //
 5 //  Created by shunagao on 15/8/31.
 6 //  Copyright © 2015年 shunagao. All rights reserved.
 7 //
 8 
 9 #include <iostream>
10 using namespace std;
11 
12 class Matrix
13 
14 public:
15     int n;
16     int **m;
17     Matrix(int num)
18     
19         m=new int*[num];
20         for (int i=0; i<num; i++) 
21             m[i]=new int[num];
22         
23         n=num;
24         clear();
25     
26     void clear()
27     
28         for (int i=0; i<n; ++i) 
29             for (int j=0; j<n; ++j) 
30                 m[i][j]=0;
31             
32         
33     
34     void unit()
35     
36         clear();
37         for (int i=0; i<n; ++i) 
38             m[i][i]=1;
39         
40     
41     Matrix operator=(const Matrix mtx)
42     
43         Matrix(mtx.n);
44         for (int i=0; i<mtx.n; ++i) 
45             for (int j=0; j<mtx.n; ++j) 
46                 m[i][j]=mtx.m[i][j];
47             
48         
49         return *this;
50     
51     Matrix operator*(const Matrix &mtx)
52     
53         Matrix result(mtx.n);
54         result.clear();
55         for (int i=0; i<mtx.n; ++i) 
56             for (int j=0; j<mtx.n; ++j) 
57                 for (int k=0; k<mtx.n; ++k) 
58                     result.m[i][j]+=m[i][k]*mtx.m[k][j];
59                    
60             
61         
62         return result;
63     
64 ;
65 int main(int argc, const char * argv[]) 
66     unsigned int num=2;
67     Matrix first(num);
68     first.m[0][0]=1;
69     first.m[0][1]=1;
70     first.m[1][0]=1;
71     first.m[1][1]=0;
72     int t;
73     cin>>t;
74     Matrix result(num);
75     result.unit();
76     int n=t-2;
77     while (n) 
78         if (n%2) 
79             result=result*first;
80             
81         first=first*first;
82         n=n/2;
83     
84     cout<<(result.m[0][0]+result.m[0][1])<<endl;
85     return 0;
86