吴恩达《机器学习》课程总结_线性代数回顾

Posted 2022-05-12 henuliulei

学过线性代数的人，这节课内容完全没必要看

Q1矩阵和向量

几行几列即为矩阵。Ａ_ij表示第i行第j列。

 

只有一行或者一列的称为向量，向量是一种特殊矩阵。一般向量指的是列向量。

 

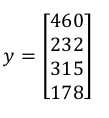
Q2加法和标量乘法

加法：元素对应相加。

 

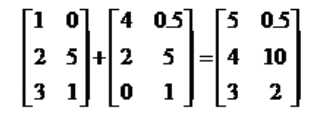
标量乘法：标量和矩阵每一个元素相乘。

 

 

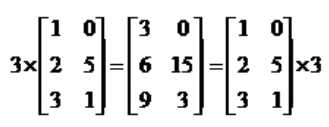
Q3矩阵向量乘法

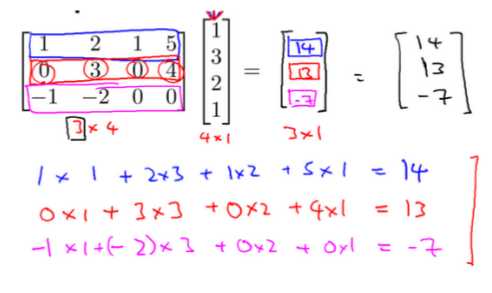
Q4矩阵乘法

要求：第一个矩阵的列数等于第二个矩阵的行数，如ｍ x n矩阵与ｎx 1矩阵相乘，结果为第一个矩阵的行数乘以第二个矩阵的列数。

结果Ｃij是第一个矩阵第i行和第二个矩阵第j列对应元素相乘求和的值。

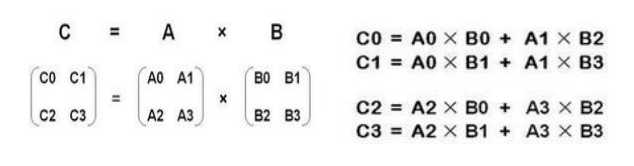
Q5矩阵乘法的性质

不满足交换律：ＡｘB != B x A。

满足结合律:(A x B) x C=A x (B x C)。

单位矩阵I：是对角线为１，其他都为零的方阵。任何矩阵于单位矩阵相乘，矩阵保持不变。

Q6逆、转置

如果矩阵Ａ的逆矩阵存在，则ＡＡ^-1=Ａ^-1A=I。

如果Ａ的转置矩阵是Ｂ，则Ａ矩阵第i行第j列元素与Ｂ矩阵第j行第i列元素相等。记Ａ^Ｔ＝Ｂ。

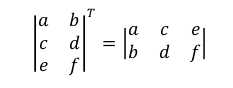
转置矩阵的一些性质：

（Ａ±Ｂ）^T=(Ａ^Ｔ±B^Ｔ)。

（ＡｘB）^T=B^Ｔx Ａ^Ｔ。

（Ａ^Ｔ）^T=A。

（ＫＡ）^Ｔ=KA^T。

英语名词

 

linear algebra   ---线性代数
matrix element	---矩阵元素
3 by 2 matrix   ---3*2矩阵
identity matrix	---单位矩阵
associative property	---结合律
inverse	---倒数，逆
square matrix 方阵
notation	---符号
hypothesis   ---假设
multivariate linear regression 多元线性回归